Основные сведения. ЭМ явления в макроскопической теории классифицируются следующим образом: электростатическое и магнитостатическое поля

ЭМ явления в макроскопической теории классифицируются следующим образом: электростатическое и магнитостатическое поля, стационарное ЭМП, квазистационарное ЭМП и быстропеременное ЭМП.

Электростатическое и магнитостатическое поля.Статические явления характеризуются постоянством величин ЭМП во времени (¶/¶ t = 0) и отсутствием макроскопических электрических токов. При этих условиях систему уравнений Максвелла можно разделить на электростатическую и магнитостатическую подсистемы. В этом случае электрические и магнитные явления можно рассматривать независимо друг от друга [1].

Уравнения электростатики (магнитное поле отсутствует):

; . (10.1)

Внутри проводящей среды по условиям электростатики электрическое поле отсутствует (поскольку = 0, то 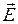= 0, а значит, и ). Поскольку , внутри проводящей среды заряды различных знаков компенсируют друг друга. В условиях электростатики нескомпенсированные электрические заряды сосредотачиваются на поверхности проводника, где их распределение характеризуется поверхностной плотностью заряда s_S.

Для того чтобы защитить некоторый объем от действия электростатического поля, его необходимо окружить проводящей поверхностью, которую называют электростатическим экраном.

При анализе электростатического поля используют скалярный электрический потенциал j(r) (см. тему 11), который записывается в виде .

Для точечного заряда получается такая зависимость :

. (10.2)

В электростатическом поле нет движения энергии. Полная энергия электростатического поля в объеме V [1–6, 11]) будет равна

. (10.3)

Первое слагаемое в уравнении (10.3) соответствует непрерывному распределению заряда в диэлектрике, а второе – дискретным зарядам системы из n проводящих тел.

Отношение заряда уединенного проводящего тела к его потенциалу есть величина постоянная, называемая электрической емкостью [1].

В случае системы заряженных тел, находящихся в однородном диэлектрике, необходимо учитывать не только собственную, но и взаимную емкость тел.

В случае двух проводников получается конденсатор.

Энергия электростатического поля конденсатора (q = q₁ = –q₂) [1, 11]

. (10.4)

При расчете электростатических полей часто используют теорему Гаусса (2.3) и метод зеркальных изображений.

Уравнения магнитостатики (электрическое поле отсутствует) :

div 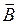=0 ; rot =0 . (10.5)

Магнитостатическое поле обусловлено неподвижными постоянными магнитами. В первом приближении намагниченность этих магнитов можно представить как сумму постоянной (собственной) намагниченности, которая не зависит от , и индуцированной, зависящей от линейно.

С помощью введения понятия магнитных зарядов (r_М =div ) задачи магнитостатики можно решать методами электростатики. Для этого необходима замена переменных: 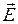® , e_а ®m_а, r_Э ®r_М. Магнитные заряды являются фиктивными и вводятся как эквивалент действия элементарных электрических токов при отсутствии внешнего магнитного поля (см. тему 11) [1, 11].

Стационарное и квазистационарное ЭМП.В отличие от электростатического поля стационарное электрическое поле существует кроме диэлектрика еще и в проводнике при наличии постоянного тока проводимости (s = const):

rot 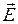= 0, ; . (10.6)

Объемные электрические заряды могут существовать только в тех областях проводящей среды, где отсутствуют сторонние токи.

В некоторых случаях для стационарного электрического поля в области, свободной от сторонних зарядов и токов, применим метод электростатической аналогии, который позволяет свести задачу стационарного электрического поля к задачам электростатики. В этом случае граничные условия для составляющих вектора плотности тока аналогичны граничным условиям для вектора электрической индукции. Переход к уравнениям электростатики для систем с одинаковыми геометрическими размерами осуществляется с помощью следующей замены переменных [1–4] :

; ; ; . (10.7)

Метод электростатической аналогии используется при анализе ЭМП линий передачи с Т-волной (см. тему 17); электростатическая аналогия позволяет экспериментально исследовать сложные электростатические поля с помощью их моделирования в ванне с электролитом [1].

Уравнения стационарного магнитного поля записываются в виде

div 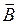= 0 ; . (10.8)

В уравнениях (10.8) уже заметна определенная связь между электрическим и магнитным полями.

Наиболее распространенной задачей является определение стационарного магнитного поля по заданному распределению токов. Для изотропной линейной однородной среды анализ ЭМП удобно проводить с помощью 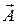(см. тему 11).

Энергия стационарного магнитного поля

. (10.9)

Сравнивая формулу (10.9) с (10.3), можно заметить определенное сходство уравнений стационарного магнитного поля с уравнениями электростатики.

Полную энергию стационарного магнитного поля системы из n контуров с токами удобно выражать через токи и индуктивности:

, (10.10)

где Y_k – потокосцепление k-го контура; L_k – собственная индуктивность k-го контура; M_jk – взаимная индуктивность j-го и k-го контуров [1–6].

Первое слагаемое (10.10) представляет сумму собственных энергий магнитных полей контуров, а второе слагаемое (10.10) – взаимную энергию магнитных полей, создаваемых токами в данных контурах.

С помощью анализа запаса магнитной энергии в системе можно вычислять индуктивность проводников и линий передачи Т-волны [1–3].

При анализе многосвязных линий передачи Т-волны и соединений с их использованием составляют матрицы взаимных емкостей и индуктив­ностей проводников линии на основании уравнений (10.3) и (10.10).

Квазистационарным ЭМП в области V называют ЭМП, для которого можно пренебречь волновым характером. Для квазистационарного поля время, в течение которого источники поля успевают заметно измениться, велико по сравнению со временем запаздывания волнового фронта (l/v). (l – расстояние (рис. 10.1) в области V, которое со скоростью v проходит распространяющаяся ЭМВ.)

Время запаздывания – это время, необходимое для распространения ЭМ возмущения от одного конца системы до другого [6].

Для квазистационарного ЭМП справедливы следующие соотношения:

,

. (10.11)

В случае монохроматических колебаний плоская волна превращается в колебание во времени:

cos [w(t–l/v)] = cos (wt),

откуда следует еще одно условие квазистационарности поля:

wl/v<<1 Þ l<<l.

Таким образом, при монохроматических процессах ЭМ системы можно исследовать с помощью законов квазистационарного ЭМП, если протяженность систем много меньше длины волны [1, 11].

Например, на рис. 10.1 для объекта с максимальным размером l условие квазистационарности выполняется для lнч, для lовч погрешность квазистационарного приближения уже обнаруживается, а при lсвч условие квазистационарности не выполняется, и необходимо учитывать волновой характер ЭМП.

На рис. 10.2 показано, как с ростом частоты длина проводников влияет на параметры системы. Как известно, на низких частотах проводники печатных плат и соединительных линий могут иметь произвольные длины, которые определяются лишь удобством монтажа элементов и конструктивных соединений.

Второй проводник на рис. 10.2 длин­нее первого на 2L2, что приводит к задержке фазы Δφ = 2βL2 отно­сительно первого проводника. Например, Δφ = 90° (π/2) при β L2 = π/4 и, следовательно, при L2 = 5 мм указанный Δφ достигается при l = 4 см (L2/l = 1/8). С дальнейшим уменьшением l Δφ увеличивается и, наоборот, при увеличении l Δφ уменьшается. Например, если увеличить l на порядок: l = 40 см, то Δφ = 9º, и часто этим набегом фазы можно пренебречь.

Для квазистационарного ЭМП возможен переход от уравнений электродинамики к уравнениям электротехники (законы Г. Р. Кирхгофа) [1, 7].

Покажем, что основные уравнения электротехники являются следствием системы уравнений Максвелла (связь с законом Ома рассмотрена ранее (1.2)).

Напомним, что в электротехнике и теории цепей считается, что элементы цепи имеют сосредоточенные параметры и взаимодействуют только через соединительные проводники.

Для вывода формулировки первого закона Кирхгофа рассмотрим узловую точку (рис. 10.3), окруженную сферой S, в которую втекают и вытекают токи I₁, I₂,…, I_n [1, 7].

Запишем уравнение (2.5) с учетом стороннего тока (2.18) и применим к данному уравнению операцию «дивергенция», а затем проинтегрируем по объему V, охватываемому поверхностью S:

. (10.12)

С учетом того, что , преобразуем (10.12) с помощью теоремы Остроградского – Гаусса [1] :

. (10.13)

В электротехнике считают, что проводники в области S (рис. 10.3) взаимодействуют только в узловой точке, но между собой через пространство не взаимодействуют; поэтому током смещенияпренебрегаем [1, 7]. Токи проводимости существуют только в проводниках, что позволяет интегрирование по поверхности S в (10.13) заменить суммой интегралов по площади поперечного сечения каждого проводника.

(n=n1+n2) , (10.14)

В итоге получаем формулировку первого закона Кирхгофа: , – «сумма токов в узловой точке электрической цепи равна нулю».