Типы лазеров и их параметры

Создание лазеров является одним из наиболее значительных достижений современной науки. На стыке ряда наук — квантовой механики, физической оптики и радиоэлектроники — родилось новое направление, называемое квантовой оптикоэлектроникой. Это направление охватывает теорию и методы создания, а также способы применения квантовых приборов оптического диапазона.

Замечательные свойства лазеров — исключительно высокая когерентность и направленность излучения, возможность генерирования когерентных волн большой интенсивности в видимой, инфракрасной и ультрафиолетовой областях спектра, получение высоких плотностей энергии, как в непрерывном, так и в импульсном режиме — уже на заре развития квантовой электроники указывали на возможность широкого их применения для практических целей. С начала своего возникновения лазерная техника развивается исключительно высокими темпами. Появляются новые типы лазеров и одновременно усовершенствуются старые: создаются лазерные установки с необходимым для различных конкретных целей комплексом характеристик, а также различного рода приборы управления лучом, всё более и более совершенствуется измерительная техника. Это послужило причиной глубокого проникновения лазеров во многие отрасли народного хозяйства, и в частности в машино- и приборостроении.

Применение различных типов лазеров и правильная их эксплуатация невозможны без четкого представления о принципах работы оптических квантовых генераторов и об основных физических явлениях, в них происходящих. Преимущества и перспективность использования лазеров в машино- и приборостроении определяются не только прогрессом в области собственно лазерной техники, но и умелым, научно обоснованным выбором оптимальных для каждого конкретного применения режимов работы лазера и параметров его излучения [33].

Промышленная обработка материалов стала одной из областей наиболее широкого использования лазеров. Лазерный луч применяется для резания и сваривания материалов, сверления отверстий и термообработки, обработки тонких металлических и неметаллических плёнок получения на них рисунков и микросхем. Лазерная обработка материалов позволила повысить эффективность и конкурентоспособность по сравнению с другими видами обработки.

Большую ценность представляет лазер для целей неразрушающего контроля качества изготовления различных материалов и изделий в машино- и приборостроении. В настоящее время нашли применение методы лазерного контроля по оптическому поглощению, эллипсометрический, голографический, фотоэлектрический и методы на основе магнито- и электрооптических эффектов.

Успешно применяются лазеры для ионизации вещества в масс-спектроскопии с целью определения элементного состава вещества.

Все окружающие нас тела состоят из элементарных частиц атомов или из групп определённым образом объединённых атомов — молекул. Любая молекула состоит из совокупности электронов и атомных ядер, движение и взаимное расположение которых определяет значение внутренней энергии молекулы. Каждый атом или молекула могут обладать различными, но вполне определёнными значениями энергии, т.е. находиться в том или другом энергетическом состоянии. Таким образом, их внутренняя энергия квантована.

В квантовой электронике обычно имеют дело не с одним атомом, а с весьма большим его числом, представляющим собой некоторый ансамбль частиц. Так, в одном кубическом сантиметре газа при нормальных условиях находится 2,7 * 10¹⁹ см^-3 атомов (число Лошмидта).

Частицы, входящие в состав ансамбля, непрерывно взаимодействуют между собой, что приводит к вполне определённому распределению их энергии. Такое распределение частиц при термодинамическом равновесии подчиняется закону Больцмана, согласно которому вероятность пребывания атома в состоянии i с энергией W, т. е. вероятность нахождения его на каком-либо энергетическом уровне i,

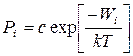, (2.3.1)

где: с — константа;

Т — абсолютная температура;

k = 1,38 10^-23 Дж/К — постоянная Больцмана.

Таким образом, из общего числа частиц ансамбля Nо на уровне i находится:

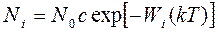. (2.3.2)

Отношение числа частиц, пребывающих в состоянии с энергией W_m‚ к числу частиц с энергией W_n равно:

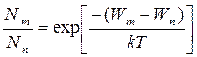. (2.3.3)

В случае, если одному энергетическому уровню атома соответствует несколько различных его устойчивых состояний, то данный энергетический уровень называется вырожденным. Число g различных независимых состояний с одинаковым значением энергии определяет кратность вырождения, или статистический вес, уровня. Вырождение связано с наличием у системы симметрии.

Отношение населённостей двух уровней m и n при их статистических весах и определятся следующим образом:

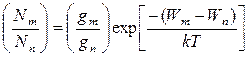. (2.3.4)

Из (2.3.3) и (2.3.4) следует, что при термодинамическом равновесии число частиц, находящихся на верхнем энергетическом уровне, оказывается значительно меньше, чем на нижнем; при этом чем выше располагается энергетический уровень, тем меньше находится на нём частиц.

Свет представляет собой электромагнитные волны. Энергия электромагнитного поля света также квантована. Каждый квант энергии излучения — фотон — равняется hν, где ν -частота колебаний,

h = 6,625 10^-34 Дж·с — постоянная Планка.

Таким образом, энергия фотона прямо пропорциональна частоте и возрастает с уменьшением длины волны.

Атом может взаимодействовать с электромагнитным излучением, изменяя при этом своё энергетическое состояние и совершая переход с одного уровня на другой.

При этом поглощении электромагнитной энергии происходит переход атома на более высокий энергетический уровень. При переходе на нижний энергетический уровень происходит испускание энергии в виде кванта света.

Если атом находится в верхнем энергетическом состоянии с энергией W_m, то имеется вероятность того, что через некоторое время он перейдёт в нижнее состояние, определяемое энергией W_n‚ и при этом произойдёт излучение кванта энергии, величина которого будет равна:

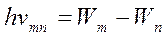. (2.3.5)

Вероятность перехода атома с одного энергетического уровня на другой имеет две составляющие. Первая зависит от свойств атома и не зависит от внешних факторов и определяет так называемое спонтанное излучение. Вторая линейно зависит от плотности энергии поля, соответствующей частоте перехода, действующего на атом извне и определяет вынужденное индуцированное излучение.

Индуцированное и спонтанное излучения впервые были рассмотрены и теоретически введены Эйнштейном. Коэффициент спонтанного перехода А_mn определяет вероятность спонтанного перехода изолированного атома в единицу времени с уровня m на уровень n. Коэффициенты вынужденного излучения В_mn и поглощения В_nm определяют вероятность соответствующих переходов в единицу времени при воздействии на атом потока энергии со спектральной плотностью, равной единице. Соотношение между коэффициентами спонтанного и вынужденного излучений имеет вид:

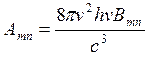. (2.3.6)

Так, при частоте v=6 10¹⁴ с^-1 (длина волны λ равна 0,5 мкм) и плотности возбуждающего потока 1 мкВт/см², А_mn ≈ 10^-6 В_mn. Видно, что вынужденное излучение значительно преобладает над спонтанным.

Представим теперь ансамбль, состоящий из Nо атомов, на который действует электромагнитное излучение с частотой v_mn и спектральной плотностью потока U_v. Пусть N_m и N_n — числа атомов, находящихся соответственно на верхнем и нижнем энергетических уровнях. Тогда число поглощённых ансамблем фотонов за время dt равно числу переходов атомов с уровня n на уровень m, будет равно: N_nB_mnU_vdt.

При этом энергия поглощения имеет вид:

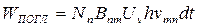. (2.3.7)

Общее число переходов атомов, как спонтанных, так и вынужденных, с уровня m на уровень n за то же время будет:

.

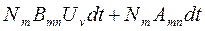Так, как A_mn<< В_mn, то излучённая ансамблем энергия имеет вид:

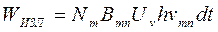. (2.3.8)

Если W_ИЗЛ будет больше, чем W_ПОГЛ то можно ожидать усиления интенсивности падающей на систему электромагнитной волны.

Тогда,

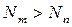. (2.3.9)

Таким образом, видно, что условием усиления электромагнитной волны ансамблем атомов является распределение в нём населённостей по энергетическим уровням. Число молекул на верхнем энергетическом уровне должно быть больше, чем на нижнем. Это является основным условием работы всех типов квантовых усилителей и генераторов.

Мгновенная мощность излучения ансамблем будет равна:

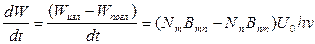. (2.3.10)

Из (2.3.10) следует, что мощность излучения пропорциональна разности населённостей энергетических уровней. Поэтому при создании квантового генератора необходимо прежде всего выполнение таких условий, при которых в ансамбле частиц населённость верхнего энергетического уровня будет по возможности больше населённости нижнего. Для этого необходимо предварительно подвергнуть ансамбль соответствующему воздействию, которое привело бы к должному перераспределению частиц по энергиям. Такое воздействие называется накачкой.

Каждый энергетический уровень имеет ту или иную степень разности, определяемую интервалами энергии ΔW_m, ΔW_n. Поэтому при переходе с одного уровня на другой по существу происходит излучение в определённом интервале частот Δv_mn. Интенсивность излучения е пределах этого интервала не постоянна. Эти факторы определяют ширину спектральной линии излучения.

С точки зрения квантовой механики естественная ширина спектральной линии вызвана неопределённостью в энергии стационарных состояний атома. Из принципа неопределённости следует, что энергия системы ΔW определяется соотношением:

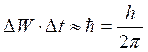, (2.3.11)

где: Δt - время существования системы;

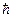- постоянная Планка.

Если вероятность перехода с уровня m на уровень n есть A_mn, то среднее время жизни атома обратно пропорционально перехода, т.е. Δt=1/A_mn. Но так как W=hv_mn, a ΔW=hv_mn, тогда из (2.3.11) следует:

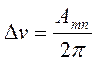. (2.3.12)

Чем больше время жизни атома по отношению к данному переходу, тем уже интервал значений ΔW и тем меньше размыт данный уровень, а следовательно, соответствующая спектральная линия будет уже.

Распределение интенсивности по частотам, присущим данной спектральной линии, определяет форму спектральной линии, которая представлена некоторой нормированной функцией, S(v₁v₀), где v₀ — резонансная частота:

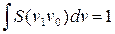, (2.3.13)

При естественной ширине спектральной линии:

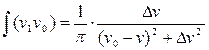, (2.3.14)

Ширина спектральной линии может изменяться при процессах, ограничивающих время жизни возбуждённого состояния. К таким процессам относятся различные виды соударений (например, соударение излучающего атома в газе с нейтральными атомами, ионами и электронами, со стенками сосуда), а также взаимодействие излучающего атома с кристаллической решёткой в твёрдом теле. Однако и в этих случаях форма спектральной линии определяется уравнением (1.3.14), получившем название лоренцевой формы.

Частотная характеристика при соударениях имеет вид:

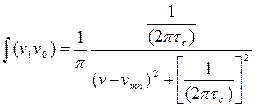, (2.3.15)

где τ_с — среднее время пробега между соударениями.

Поскольку частота соударений зависит от давления газа, то ширина линии излучения также зависит от давления.

В газе при достаточно низком давлении форма линии будет определяться эффектом Донлера. В этом случае форма спектральной линии будет гауссовой:

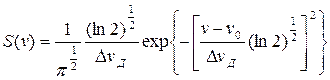. (2.3.16)

В реальных условиях одновременно действуют механизмы, определяющие как лоренцеву, так и гауссову формы. Учитывая реально существующую частотную характеристику, возвратимся к формуле (2.3.10), определяющей мощность излучения. Тогда (2.3.10) примет вид:

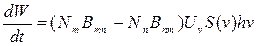. (2.3.17)

Откуда видно, что возможно усиление электромагнитных волн в случае индуцированного излучения в некотором ансамбле атомов при условии, что большинство атомов находится в верхнем из двух энергетических состояний, связанных соответствующим переходом. Однако оказывается, что во многих случаях для достижения значительного усиления требуется большая длина пути.

Изменение интенсивности электромагнитной волны при прохождении её через среду определяется формулой:

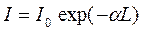, (2.3.18)

где: L — длина пути;

α =(N_n – N_m) σ_mn — коэффициент поглощения;

σ_mn - эффективное сечение взаимодействия фотона с атомом.

При наличии инверсии N_m > N_n коэффициент α имеет отрицательное значение и среда работает как усиливающая. Степень усиления определяется произведением αL следовательно, получение значительного усиления на небольшом пути возможно только при очень больших значениях коэффициента α, т. е. при достижении очень высокой инверсии.

Однако, если ансамбль поместить в резонатор, то излучение, прежде возможным усиление поступающего в резонатор излучения. Всеми характеристиками резонатора оптического диапазона обладает интерферометр Фабри-Перо. В лазерах применяются резонаторы Фабри-Перо как с прямоугольными, так и с круглыми плоскими зеркалами, а также другие типы открытых резонаторов: конфокальные, в которых сферические зеркала располагаются на расстоянии, равном их радиусу кривизны; резонаторы, в которых одно зеркало является плоским, а другое сферическим, и т. д.

Весьма важным параметром резонатора является его добротность, которая определяется потерями в резонаторе. Добротность резонатора ‘ опре деляется как:

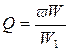, (2.3.19)

где: ω - круговая частота колебаний;

W — энергия, запасённая в резонаторе;

W₁ - энергия, теряемая за 1 сек.

Из (2.3.19) следует, что потеря мощности в резонаторе обратно пропорциональна его добротности.

Добротность оптического резонатора, если пренебречь поглощением среды, заполняющей резонатор, определяется формулой:

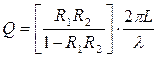, (2.3.20)

где: R₁, R₂ —коэффициенты отражения зеркал;

λ - длина волны.

При двух одинаковых зеркалах

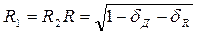, (2.3.21)

где: δд_, δ_R —относительные потери мощности в следствии дифракции и отражения соответственно.

В случае, когда потери малы (δ_д + δ_R)<<1, имеем:

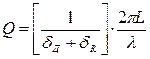, (2.3.22)

Ширина собственной линии резонатора равна:

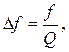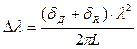или . (2.3.23)

Наличие активной среды сильно изменяет добротность. В этом случае ширина спектральной линии рабочего перехода значительно больше расстояния между соседними частотами резонатора, поэтому спектр излучения состоит из нескольких резонансных частот. Линии излучения будут располагаться по всей ширине спектральной линии только в том случае, если уровень накачки обеспечивает условие генерации по всему контуру линии. Уровень накачки для возникновения генерации должен быть достаточно большим, чтобы перекрыть потери в резонаторе, что будет вполне определённой (минимальной) (пороговой) инверсии и соответствующей ей мощности накачки, ниже которых генерации не возникает.

Мощность, излучаемая ансамблем, находящимся в резонаторе, согласно (2.3.17) равна:

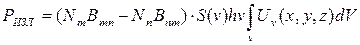. (2.3.24)

Потери в резонаторе согласно (2.3.19):

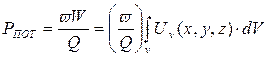. (2.3.25)

Условием порогов генерации будет являться Р_изл.> P_пот., т.е.

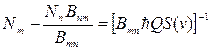. (2.3.26)

Таким образом, если постепенно увеличивать мощность накачки, то генерация возникает только при достижении вполне определённой её величины, определяемой (2.3.26). После достижения порога генерации выходная мощность возрастает с увеличением мощности накачки приблизительно по линейному закону. Далее вследствие того, что населённость внешнего энергетического уровня приближается к населённости нижнего, увеличение мощности замедляется и затем наступает насыщение (рис.2.3.1).

Рис. 2.3.1.Зависимость выходной мощности лазера от мощности накачки