Б) Навигационные параметры взаимозависимы
При взаимозависимых навигационных параметрах расчет элементов эллипса существенно усложняется:
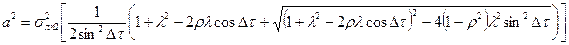 ; (2.3.4)
; (2.3.4)
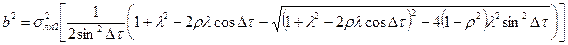 ; (2.3.5)
; (2.3.5)
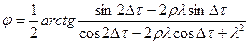 (2.3.6)
(2.3.6)
| I «_ |
| а* = а* |
- 2pXcosAr
| .(2.3.4) (23,5) (i3.fi) |
 X2 -2/>XcosAt)2 -4 (1 -р2) X2sin2At)] ;
X2 -2/>XcosAt)2 -4 (1 -р2) X2sin2At)] ;
[__J___ (1 + х2 - 2оХсо8лт -
[з 2ш2Ат
 *-Х2 - 2pXcosAf)2 - 4 (1-р'О Х2яп2Дг)1;
*-Х2 - 2pXcosAf)2 - 4 (1-р'О Х2яп2Дг)1;
.. - E!ll4.I.zirjj?J^S?,.4^.
cos2 Af — 2pXcos At + X2
Практически эти формулы могут быть использованы лишь при расчетах с помощью ЭВМ по заранее составленной программе им с помощью таблицы готовых значений элементов зллияеа»
Важно иметь в .виду, что для расчета используются полные погрешности линий положения ajm = (а2 + ol)fg2..Вместо угла пересечения линий положения здесь используется угол межщ градиентами Ато
Угол *р откладывается от второй линим положения: положительный — внутрь угла, между линиями положения,, равного в = Л г, отрицательный — внутрь угла между линиями положении, равного в = 180° —. Ат, Проложенное с помощью угла ^ направление определяет направление большом осм эллипса, если cos2^/{cos2At — 2рксо%Ат.+' X2) > 0,,:, в противном случае иаиденное направление укажет направление- малой оси.
При неизменных Ат и А изменение коэффициента каррелжрж^ -будет вызывать изменение размеров эллипса погрешностей и изменение угла его •ориентировки. При р = 1 (навигациоьшые параметры содержат только повторяющуюся погрешность, оцениваемую средним квадратическим значением ао) эллипс погрешностей превращается в отрезок прямой. данной 2aQ (полуось b в этом случае равна нулю) .
Величина отрезка а = ап и его направление определяются по формулам (2,3.4) — (23.6) после подстановки в них р =• L Эта же задача решается и графически (рис. 2.3.3): каждая линия положения смещается в сторону своего градиента на величину ojg. Отрезок OOt'9 соединяющий обезрвован-ное место с точкой пересечения смещенных линий положения, будет равен а§9 Отложив -ОО2 = я0 (от обсервации в противоположную сторону, получим от-
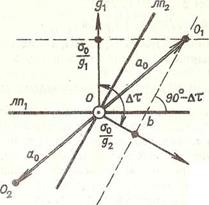 Рис. JJJ
Рис. JJJ
резок О}О2 - 2aq, в-пределах которого находится истинное место корабля с вероятностью 39,3%, ■
Если р = 1 и линии положения равноточны, то в косоугольном треугольнике Ob О х стороны Ob = Ь.Ог = o'Qlgmn Ar. Тогда но теореме косинусов получим.
_ _ _ / —. Ат _
| sec ■ |
(23:7)
Отсюда следует, что при наличии только повторяющейся погрешности более острый угол Ат предпочтительнее, чем более тупой.
Пример. В' благоприятных условиях (погрешности измерения пренебрежимо малы) измерили два пеленга на ориентиры, расположенные в секторе oj = 10°. Поправка гирокомпаса известна ориентировочно (сдгк = ^о = 2°)в "Определить среднюю квадратическую погрешность места, если расстояния до ориентиров D% « D2 = 5,7 мили» Сравнить полученный результат с погрешностью места, полученного по ориентирам, расположенным в секторе w = 170° нч тех же f зестоячиях
г\пени . Piv т »" ^ ч гирокомпаса из"с,/тна ориентировочно, а но»
гг>олшогги измгрий^л л?~№ •»* iff корежимо '^ я,"^ (а^ 0),то коэффициент/7
взаимной корреляции р '^ I. Поэтому средняя квадратнческая погрешноро»
места характеризуется линейной величиной aOj вычисляемой дая равнотршых
линий положения по формуле (2.3.7): ■ ~~ "
-- вычисляют градиенты: ^j = ^2 = ^ = 57,3/5S7 s 10,0°/мили;
— рассчитывают среднюю квадратическую погрешность линий положения:
а = ао = а = а /^ = 2/10 = 0,2 мили;
ЛП| jm1 " ЛП
— вычисляют а0 для Ат = аз = 10°:
я0 =0,2/cos5° = 0,2/0,996« 0,2 mmjim;
Дата добавления: 2015-04-21; просмотров: 1921;
