ЭЛЛИПС ПОГРЕШНОСТЕЙ

Случайные погрешности навигационных параметров вызывают случайные смещения навигационных изолиний (линий положения). В результате обсер-вованное место оказывается смещенным относительно истинного по случай­ному направлению и на случайную величину. Предсказать случайную вектор­ную погрешность места невозможно. Поэтому погрешность места учиты­вается в вероятностном смысле в виде указания площади, в пределах которой находится истинное место корабля с определенной вероятностью.

В теории вероятностей показывается, что при нормальном рассеивании точек на плоскости истинная безошибочная точка с некоторой вероятностью находится в пределах площади эллипса соответствующих размеров, прове­денного относительно наиболее вероятного места этой точки. При оценке точности места корабля за центр эллипса принимают обсервованное- или, в общем случае, вероятнейшее место корабля. Эллипсов, подобных друг другу, можно провести бесчисленное множество (рис 2.2.1), и каждому из них соответствует своя вероятность невыхода истинного места корабля за пределы данного эллипса. Чем больше размеры эллипса, тем выше вероят­ность нахождения безошибочного места в пределах его площада.

Так как эллипсы рассеивания характеризуют возможные ошибки места, то их называют эллипсами погрешностей.

Рисунок 2.2.1.

При взаимонезависимых погрешностях навигационных параметров урав­нение эллипса погрешностей имеет вид

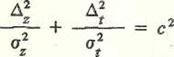
(2.2.1)

где ∆_z, ∆_t— случайные погрешности места по направлению главных осей эллипса;

σ_z , σ _t . — средние квадратические погрешности места по направлению главных осей;

с — коэффициент, характеризующий размеры эллипса (0 < с < ∞).

Главными полуосями эллипса погрешностей являются величины

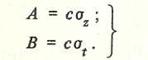
(2.2.2)

За показатель точности места принимают эллипс с коэффициентом с = 1, т.е. эллипс с главными полуосями, равными А = σ_z , В= σ _t . Такой эллипс называют средним квадратическим эллипсом. Иными словами, средний квадратический эллипс погрешностей — это эллипс, главные полуоси которого равны средним квадратическим погрешностям места по направлению главных осей (рис. 2.2.2).

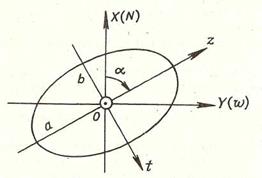
Рис. 2.2.2

Большую главную полуось среднего квадратического эллипса погреш­ностей принято обозначать буквой а (а= σ_z ), малую — буквой b(b = σ _t ).

Ориентировка эллипса на плоскости характеризуется направлением большой оси относительно меридиана — углом α. В некоторых случаях указывают ориентировку не большой, а малой оси, и за начальное направление принимают не меридиан, а направление одной из изолиний.

Главные полуоси эллипса а, b и угол ориентировки эллипса αназывают элементами среднего квадратического эллипса погрешностей.

Главные полуоси любого другого эллипса погрешностей выражаются через элементы среднего квадратического эллипса с помощью формул

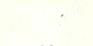
А = са;

В= cb,(2.2.3)

т.е. коэффициент с показывает, во сколько разглавные полуоси данного эллипса погрешностей больше (меньше) главных полуосей среднего квадратического эллипса.

Вероятность нахождения истинного места корабля в пределах площади эллипса с заданными полуосями А = са и В = сb рассчитывается по формуле

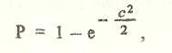(2.2.4)

где е — основание натурального логарифма.

Формула (2 .2.4) получена в результате интегрирования функции, выражающей плотность двухмерного нормального распределения. При этом за область интегрирования принят эллипс с заданным коэффициентом с.

Единственный аргумент для расчета вероятности — величина с, характе­ризующая размеры эллипса относительно среднего квадратического эллипса погрешностей.

Если с = 1, т.е. если А = а и В = b (средний квадратический эллипс), то формула (2.2.4) дает результат Р = 0,393. Это значит, что вероятность нахож­дения истинного места, корабля в пределах среднего квадратического эллипса погрешностей составляет 39,3%.

Если с = 2, т.е. если: А = 2а и В =2b (удвоенный средний квадратический^: эллипс),

то Р = 0,865.

Если с = 3, т.е. если А = 3а и В =3b (утроенный средний квадратическийэллипс),

то Р = 0,989.

Расчеты показывают, что практически истинное место корабля не выхо­дит за пределы площади утроенного среднего квадратического эллипса по­грешностей.

Расчет по формуле (2.2.4) упрощается с помощью микрокалькулятора или табл. 1-а МТ-75.

Если требуется определить размеры эллипса погрешностей, соответству­ющего заданной вероятности, то вначале вычисляют величину с, а затем и искомые размеры эллипса: А = са и В=сb. Величину с находятиз выражения (2.2.4):

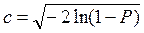(2,23)

Необходимые для вероятностной оценки точности места элементы сред­него квадратического эллипса рассчитываются по правилам, изложенным в последующих параграфах.

Пример. Определить вероятность нахождения истинного места корабля в пределах площади эллипса с главными полуосями А = 6,5 мили и В = 5,0 миль, если главные полуоси среднего квадратмческого эллипса погреш­ностей равны: а = 2,6 мили, b = 2,0 мили.

Решение:

- рассчитывают коэффициент с:

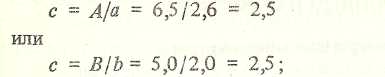
- по формуле (2.2.4) с помощью микрокалькулятора или табл. 1-а МТ-75 вычисляют искомую вероятность Р = 0,956. Это значит, что истинное место корабля находится в пределах заданного эллипса с вероятностыо 95,6%.

Пример. Определить размеры эллипса - главные полуоси А и В, в преде­лах которого находится истишюе место корабля с вероятностью 0,95, если а = 4,0 каб, b =2,5 каб.

Решение;

- по формуле (2.2.5) или с помощью табл. 1-а МТ-75 (обратным вхо­дом) определяют величину

с = 2,45;

- вычисляют искомые полуоси эллипса погрешностей: А=са=2,45•4,0=
9,8 каб; В = сb= 2,45 • 2,5 = 6,12 каб.

При решении некоторых задач навигации требуется знать среднюю квадратическую погрешность места корабля по заданному направлению — по ли­нии L (например, по направлению на навигационную опасность). Эта погреш­ность численно равна квадратической сумме проекций главных полуосей среднего квадратического эллипса на заданное направление (рис. 2.2.3):

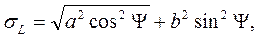(2.2.6)

где Ψ — угол между большой осью и линией заданного направления.

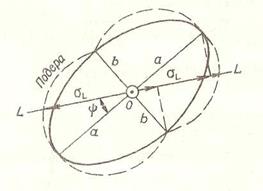
Рис. 2.2.3

Концы средних квадратичееких погрешностей σ_L, взятых по всем, направнениям, образуют геометрическое место точек, называемое подерой эллипса погрешностей.

Эллиптическая оценка точности места используется при автоматизиро­ванных расчетах надёжности и точности кораблевождения и при предварительных расчётах точности плавания в узкости и по фарватерам.

2.3. РАСЧЕТ ЭЛЕМЕНТОВ СРЕДНЕГО КВАДРАТИЧЕСКОГО ЭЛЛИПСА ПОГРЕШНОСТЕЙ ПРИ ОПРЕДЕЛЕНИИ МЕСТА ПО ДВУМ НАВИГАЦИОННЫМ ПАРАМЕТРАМ