А) Навигационные параметры взаимонезависимы
Главные полуоси среднего квадратического эллипса погрешностей при определении места по двум взаимонезависимым навигационным параметрам могут быть определены на основе использования теоремы Аполлония: для любого эллипса справедливы следующие соотношения между главными полуосями а и b ипроизвольно взятой парой сопряженных полудиаметров эллипса l1 и l2:

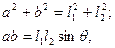
где θ — угол между сопряженными полудиаметрами.
Напомним, что два полудааметра эллипса являются сопряженными, если любой из них параллелен касательной к эллипсу, проведенной через конец другого полудиаметра.
При определении места по двум линиям положения сопряженными полудиаметрами являются векториальные средние квадратические погрешности линий положения σl1 и σl2. Поэтому

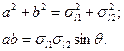
Решив эти уравнения совместно, получим

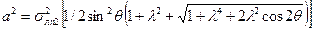
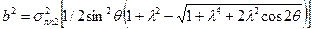 (2.3.1)
(2.3.1)
Здесь
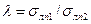
Обозначим выражения; заключенные в квадратные скобки, через 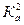 и
и 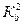 соответственно. Тогда
соответственно. Тогда
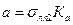 ;
; 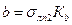 (2.3.2)
(2.3.2)
Где σлп2 – СКП второй линии положения, которая стоит в знаменателе величины λ.
Ориентирование большой оси эллипса относительно второй линии положения — угол φпри взаимонезависимых линиях положения определяется по формуле
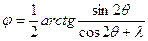 (2.3.3)
(2.3.3)
Этот угол откладывают от второй линии положения внутрь угла пересечения линий положения — θ.
Значения Ка, Кь и φ определяют с помощью таблицы приложения 5 МТ-75.
Расчет производят в следующем порядке:
—по формуле σлп = σu /g вычисляют СКП линий положения;
—рассчитывают величинуλ = σлп(б) / σлп(м);
—по λ и острому углу пересечения линий положения θ с помощью таблицы приложения 5 МТ-75 определяют величины Ка Кь и φ;
—по формулам (2.3.2) вычисляют главные полуоси среднего квадратического эллипса;
—при необходимости элементы эллипса отображают на карте: большую
полуось откладывают от обсервованного места (рис. 2.3.1) в направлении φ
(в ту и другую стороны), а малую полуось — в направлении, перпендикулярном большой оси.

Рис.2.3.1
Пример. Место корабля определено по двум взаимонезависимым радиопеленгам; ЛокП=139,0° и ЛокП=299,0°. Средние квадратические погрешности линий положения σлп= 0,75 мили и σлп = 1,5 мили; угол пересечения линий положения θ = 20°. Определить' элементы среднего квадратического эллипса.
Решение:
—рассчитывают λ = 1,5/0,75 = 2,0;
—по λ = 2,0 и θ = 20° из таблицы приложения 5 МТ-75 выбирают величины Ка = 6,48; Кb = 0,9; φ = 4°;
—рассчитывают главные полуоси: а=0,75•6,48=4,9мили; b=0,75•0,9=0,68 мили.
Средний, квадоатический эллипс погрешностей при взаимонезависимых навигационных параметрах может быть построен приближенно графическим способом (рис. 2.3.2): в районе обсервации производится смещение линий
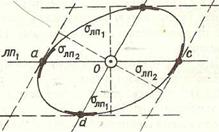
Рис. 2.3.2
| 9г |
положения параллельно самим себе на величины σлп1 = σu1 /g2 и σлп2 = σu2 /g2 (в ту и другую стороны). В образовавшийся параллелограмм вписывается эллипс так, чтобы он касался сторон параллелограмма в точках их пересечения с линиями положения, т.е. в точках а,b,с и d.
Дата добавления: 2015-04-21; просмотров: 2164;
