Разделение электронных и колебательных движений.

Согласно адиабатическому приближению, предложенному Борном и Оппенгеймером, можно произвести разделение электронного, колеба­тельного и вращательного движения молекулы. Это происходит потому, что из-за большой разницы в массах электронов и ядер ядра движутся существенно медленнее, чем электроны.

Оценим приближенно величины энергий, соответствующих упомянутым движениям. Рассмотрим энергию движения электронов ( ).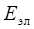

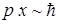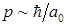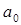где m - масса электрона, p - импульс. Используя соотношение неопределенности , мы имеем , где - боровский радиус (0,5 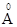). Следовательно, 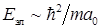. Диапазон изменений этой величины составляет 2-10 эВ. Соответствующие переходы попадают в видимую или ультрафиолетовую область спектра.

Оценим энергию колебательного движения .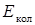

,

где M - масса ядра.

Величину k можно определить как кривизну кривой потенциальной энергии для колебаний ядер. Поскольку потенциальной энергией для колебаний ядер является электронная энергия, зависящая от координат ядер, как от параметров мы имеем кол

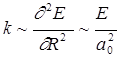
В этой формуле R обозначает координату ядра. Тогда

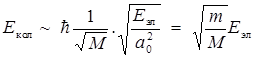
Поэтому энергия колебательного движения примерно на два порядка меньше энергии движения электронов.

Оценим энергию вращательного движения.

,

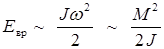где - момент инерции, угловая скорость и момент количества движения молекулы соответственно. Тогда

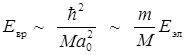
Следовательно, имеет место оценка: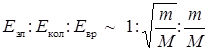

Получим теперь соотношение, связывающее волновые функции, опи­сывающие движения электронов и ядер.

Гамильтониан, описывающий электронные и ядерные движения молекулы, имеет вид:

(B1)

В этом уравнении, 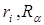- координаты электрона 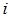и ядра .

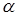Члены 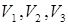описывают соответственно взаимодействия между электронами, между ядрами и между электронами и ядрами. Выделим кинетическую энергию ядер и обозначим члены гамильтониана так:

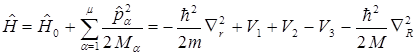(B2)

Пусть методами квантовой химии мы решили уравнение с гамильтонианом :

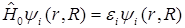(В3)

Тогда собственные функции гамильтониана (В2) будем искать в виде разложения по полному набору функции :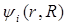

(В4)

В этом соотношении нам необходимо определить функции 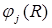. Для этого подставим выражение (В4) в уравнение Шредингера с гамильтонианом в форме (В2). При этом получим:

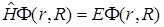(В5)

После этого в уравнение (В5) подставим соотношение (В4), умножим его на 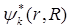и проинтегрируем по 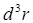(по пространственным координатам электронов и по всему пространству). Тогда получим

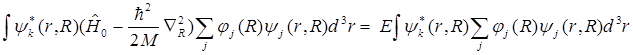(В6)

С учетом (В3) и ортогональности функции 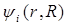, уравнение (В6) преобразуется так:

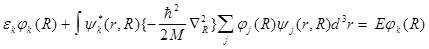(В7)

Отметим, что оператор 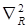во втором слагаемом левой части уравнении (В7) действует на произведение функции по правилу Лейбница. По этому учитывая ортогональность функции , уравнение (В7) можно преобразовать следующим образом:

Подчеркнутые члены уравнения (2-ое и третье слагаемые) описывают не адиабатические взаимодействия. Их можно представить в ви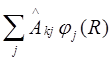де , где 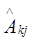- так называемый оператор неадиабатичности:

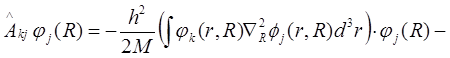
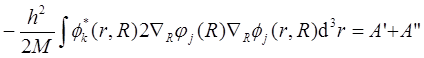
Оценим величины 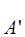и 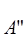по сравнению с первым членом уравнения (В8). Для этого необходимо оценить значения градиентов функци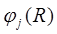й и 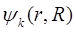по ядерным координатам. Оценим протяженность тех областей пространства, где эти функции существенно отличаются от нуля. Электронная волновая функция отлична от нуля в области порядка Боровского радиуса , ядерная вол­новая функция - в области размером порядка амплитуды колебаний ядер a. Тогда, опуская нижние индексы волновых функций, имеем следующие оценки для отношений, содержащих 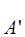и :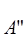

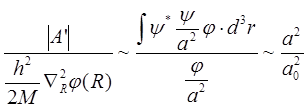
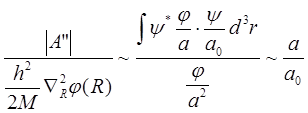
Оценим теперь величину 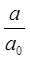. Амплитуду колебаний ядер можно определить из соотношения 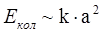, где 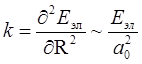. Поэтому

;

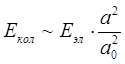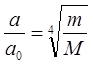
Именно такой малый параметр в теории возмущений использовали Борн и Оппенгеймер в своей первой классической работе.

Из приведенного рассмотрения ясно, когда может не выполняться адиабатическое приближение. Адиабатическое приближение не выполняется, когда электронная волновая функция сильно меняется в зависимости от ядерных координат. Это может иметь место, когда электронный уровень является вырожденным.