Процессы обогащения в безнапорной струе воды, текущей по наклонной поверхности

Обогащение в безнапорном потоке воды текущей по наклонной поверхности получило широкое распространение при обогащении руд и россыпей, содержащих золото, касситерит, вольфрамовые минералы, такие минералы редких металлов, как ильменит, рутил, циркон, танталит, колумбит, пирохлор, лопарит. Процесс основан на разнице в плотности минералов, входящих в состав руды и в способности их расслаиваться по плотности и крупности в потоке воды, текущей по наклонной поверхности и имеющей глубину не более 10-кратного размера максимального частиц.

Осуществляется этот процесс обогащения на шлюзах, желобах, винтовых, конусных сепараторах, на концентрационных столах. Общим для всех этих аппаратов, является то, что движение минеральных частиц в водной среде происходит по наклонной плоскости под углом 2…12º. Это приводит к тому, что частицы транспортируются в потоках воды за счет гидродинамической силы наклонного потока ее.

Характер движения частиц в наклонном потоке зависит прежде всего от скорости и глубины потока, крупности частиц , концентрации их в потоке и состояния поверхности, по которой они двигаются. В наклонном потоке частицы передвигаются влечением по дну агрегата за счет качения или скольжения, скачкообразно, т.е чередованием влечения и в потоке на некоторой высоте, и, наконец, движение в непрерывно-взвешенном потоке.

Частица условно шарообразной формы, двигаясь по наклонной плоскости в потоке воды, подвержены действию следующих сил (рис. 83) :

Рис. 83. Схема движения шарообразного зерна на наклонной плости в струе воды

1. Сила тяжести в воде

Р₀ = mg_o (84)

2. Сила динамического давления потока воды на частицу в направлении движения ее по наклонной плоскости

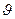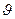P_и = ψ ( _ср - )² d²Δ, (85)

где ψ- коэффициент гидродинамического сопротивления;

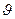_ср – средняя скорость потока при глубине потока Н и высоте от дна у;

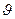- скорость движения зерна;

d – диаметр частицы;

Δ- плотность воды.

3. Подъемная сила вертикальной составляющей скорости

P_c = ψ u²_cp d² Δ (86)

4. Сила трения, направленная в сторону , противоположную перемещения частицы

Р_т = (Р_о cosα - P_c) f, (87)

где f – коэффициент трения частицы о поверхность.

С учетом всех действующих сил дифференциальное уравнение движение шарообразной частицы при достижении ею постоянной скорости ( 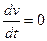) будет

mg_o sin α + ψ ( 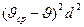Δ=( mg_o cos α - ψ Δ) f

Откуда

,

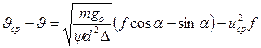Т.к. 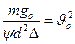по формуле Риттингера, то

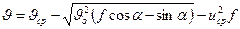(88)

Из формулы (88) следует минеральная частица будет скользить по наклонной поверхности, если

>

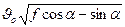и будет взвешено в потоке, если < .

Скорость продольного перемещения частицы будет увеличиваться с уменьшением .

В результате действия всех сил в движущемся потоке воды происходит распределение частиц по плотности и крупности. В нижних слоях концентрируются мелкие и крупные частицы большой плотности. Легкие минеральные частицы сносятся струей воды значительно быстрее и легче. Таким образом происходит расслаивание частиц и разделение их по плотности, т.е обогащение. Однако обогащение в безнапорных струях воды, текущей по наклонной поверхности не позволяет получать степень обогащения более 2,5-4. Поэтому перед обогащениях в наклонных потоках обычно производится предварительная классификация по крупности или по равнопадаемости, а также по развитым многостадиальным схемам.