Степень работоспособности

Поскольку заданные конструктором параметры не могут быть точно достигнуты при изготовлении, элемент ЭУ может оказаться в работоспособном состоянии, но с различным запасом работоспособности. Это объясняется, с одной стороны, неточностью изготовления элементов, а с другой – самой постановкой задач, поскольку на практике оказывается допустимой некоторая неточность в выполнении рабочих функций. Для проверяемых признаков (параметров и характеристик) вводятся эксплуатационные допуски, представляющие собой установленные опытным путем или расчетом допустимые границы изменения. Этим объясняется введение понятия области работоспособности и рассмотрение подмножества работоспособных состояний S_p. Однако не все состояния в подмножестве S_p равноценны.

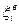Можно предположить, что чем дальше состояние s_i от границы области работоспособности нижней или верхней , тем меньше вероятность того, что объект потеряет работоспособность в ближайшее время. Удаление значений признака xi от границы области работоспособности увеличивает запас его работоспособности. Наоборот, приближение значения диагностического признака к границе области работоспособности уменьшает запас работоспособности (рис.7.5).

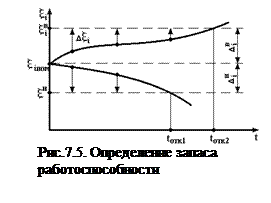Запас работоспособности 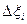через текущее значение 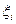и граничное (нижнее или верхнее) 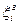может быть вычислен следующим образом:

.

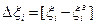Если область работоспособности разбита на ряд подобластей, то условие принадлежности значения ДП j-й подобласти записывается в виде

,

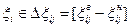где 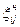и 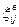– нижняя и верхняя границы j-й подобласти.

При такой оценке можно ввести диагноз типа "отлично", "хорошо", "удовлетворительно".

В связи с тем, что размерности и допустимые отклонения ДП могут быть различны при технической реализации количественной оценки изменения работоспособного состояния, удобнее пользоваться понятием степень работоспособности, которая является безразмерной величиной. Ее можно определить по одному параметру следующим образом

,

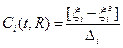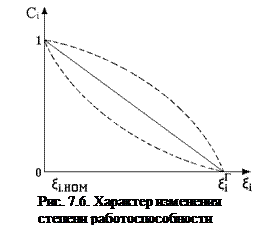где 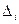– допуск (область работоспособности) на i-й диагностический параметр в области изменения; t – время; R – режим работы.

В этом случае степень работоспособности изменяется в пределах [1,0]. Если умножить на 100, то степень работоспособности оценивается в процентах.

Характер изменения работоспособности виден из рис.7.6.

Несколько сложнее оценить степень работоспособности объекта, состояние которого определяется несколькими диагностическими параметрами 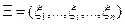. Для решения этой задачи введем число 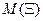таким образом, чтобы:

1) ;

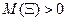2) 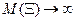, если хотя бы один параметр достигнет граничного значения ,

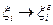3) более весомый параметр, входящий в 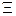, сильнее влияет на величину .

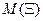Определим 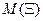как отношение двух чисел 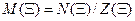. Рассмотрим произвольное число 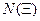такое, что

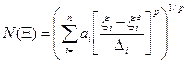, р = 1,2,... – произвольное число, а_i – весовой коэффициент.

В частных случаях

при 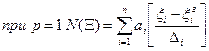– взвешенная сумма;

при 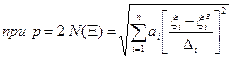– среднеквадратичное отклонение.

Построим произведение

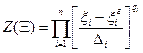,где q_i - произвольное число, выбираемое с учетом удовлетворения третьего условия.

Тогда 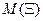при стремлении значения параметра к граничному 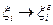будет стремиться к бесконечности, так как значение числителя при малых величинах [ 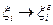] будет выше (они складываются), чем знаменателя (умножаются малые величины).

С учетом этого можно определить степень работоспособности 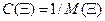, которая при изменении диагностических параметров будет изменяться в пределах [C_max,0].

В качестве весовых коэффициентов а_i при определении степени работоспособности объекта в зависимости от его особенностей могут использоваться различные показатели, получаемые расчетным или эмпирическим способами (корневой чувствительности, чувствительности к изменениям, происходящим в объекте, показатели надежности и др.)