Параметры, характеризующие состояние электроустановок.
| Вид электроустановки | Диагностические параметры | |||||
| Сопротивление изоляции | Сопротивление постоянному току | Ток несимметрии | Температура | Вибрация | Частичные разряды | |
| Генераторы переменного тока | + | + | + | + | + | + |
| Трансформаторы, автотрансформаторы, реакторы | + | + | + | + | + | + |
| Выключатели | + | + | - | - | - | + |
| Воздушные линии | + | - | - | - | - | + |
| Аппаратура управления и защиты | - | - | - | - | - | |
| Кабели | + | - | + | - | - | - |
Условия работоспособности по одному параметру непрерывных объектов задаются неравенствами, которые ограничивают его значения с одной или двух сторон:
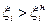 (Rи>300 МОм, сопротивление изоляции более 300 МОм, измеренное при температуре 18-200С);
(Rи>300 МОм, сопротивление изоляции более 300 МОм, измеренное при температуре 18-200С);
 (tg
(tg 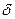 <2,5%, тангенс угла диэлектрических потерь меньше 2,5%);
<2,5%, тангенс угла диэлектрических потерь меньше 2,5%);
где 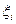 – текущее значение,
– текущее значение,  – наименьшее,
– наименьшее,  – наибольшее допустимое значение диагностических параметров.
– наибольшее допустимое значение диагностических параметров.
В большинстве случаев на диагностические параметры задаются двухсторонние ограничения вида:
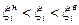 (Iн<I<1,25Iн – ток нагрузки трансформатора);
(Iн<I<1,25Iн – ток нагрузки трансформатора);
Если состояние ЭУ определяется несколькими ДП, т.е. 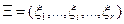 , то задачу контроля работоспособности сводят к проверке рассмотренных неравенств для каждого признака. Если хотя бы одно из неравенств не выполняется, то объект признается неработоспособным. Примером может служить синхронный двигатель серии СТД, типа 800–2, состояние которого определяется частотой вращения
, то задачу контроля работоспособности сводят к проверке рассмотренных неравенств для каждого признака. Если хотя бы одно из неравенств не выполняется, то объект признается неработоспособным. Примером может служить синхронный двигатель серии СТД, типа 800–2, состояние которого определяется частотой вращения 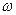 , частотой вибрации f, током утечки Iут.
, частотой вибрации f, током утечки Iут.
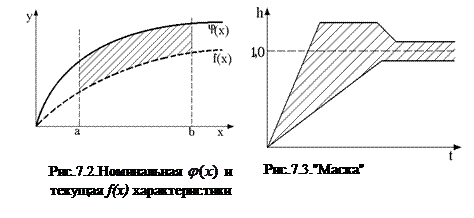
Условия работоспособности на характеристики.Если в качестве ДП используется характеристика, то оценить состояние элементов ЭУ можно или по нескольким показателям характеристики, или по отклонению текущей характеристики от номинальной. Если в качестве диагностических признаков, например, силовых трансформаторов или системы трансформатор – линия электропередачи используются показатели интенсивности высокочастотных излучений y=f(x), где x и y – соответственно входная и выходная переменные, то условия работоспособности определяются величиной отклонения текущей характеристики f(x) объекта от номинальной 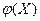 . При этом необходимо установить количественный критерий, который позволял бы оценивать сходство и различие этих характеристик. Существует несколько таких критериев:
. При этом необходимо установить количественный критерий, который позволял бы оценивать сходство и различие этих характеристик. Существует несколько таких критериев:
а) критерий среднего отклонения
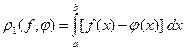 .
.
Интеграл в этом соотношении численно равен площади (рис.7.2), ограниченной функциями f(x) и 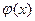 . Недостатком этого критерия является одинаковая чувствительность как к величине абсолютного отклонения, так и к длительности интервала, по которому оценивается отклонение;
. Недостатком этого критерия является одинаковая чувствительность как к величине абсолютного отклонения, так и к длительности интервала, по которому оценивается отклонение;
б) критерий среднеквадратичного отклонения
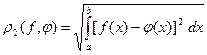 .
.
Этот критерий более чувствителен к величине отклонения, чем к длительности интервала, на котором оценивается отклонение. Он наиболее часто используется на практике;
в) критерий равномерного приближения
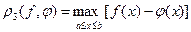 .
.
В этом случае критерием близости является их максимальное отклонение на интервале [a, b]. Если максимальное отклонение мало, то на всем интервале определения функции будут мало отличаться друг от друга.
Условие работоспособности будет выглядеть в виде неравенства
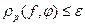 ,
,
где 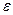 – допустимое отклонение; р = 1,2,3 – вид критерия.
– допустимое отклонение; р = 1,2,3 – вид критерия.
Допустимые отклонения на всю характеристику могут задаваться в виде маски рис.7.3).
 |
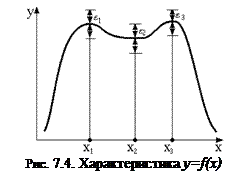
В случае, если характеристика оценивается по точкам (рис.7.4), то задается область допустимых отклонений для ограниченной совокупности точек на рабочем участке характеристики 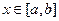 .
.
Условия работоспособности задаются для каждой точки в виде неравенства 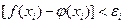 ,
,  . Если неравенства справедливы для всей совокупности рассматриваемых точек характеристики, то объект признается работоспособным.
. Если неравенства справедливы для всей совокупности рассматриваемых точек характеристики, то объект признается работоспособным.
 Для ОД, состоящего из нескольких СЕ, вектор состояния имеет вид S=(s1,...,si,...,sn). Условием работоспособности такого объекта является работоспособность каждой СЕ. Состояние СЕ имеет два исхода: работоспособна – 1, неработоспособна – 0. Тогда условие работоспособного состояния сложного объекта можно записать Sp = (1,...,1,...,1). Для каждой СЕ условия работоспособности могут
Для ОД, состоящего из нескольких СЕ, вектор состояния имеет вид S=(s1,...,si,...,sn). Условием работоспособности такого объекта является работоспособность каждой СЕ. Состояние СЕ имеет два исхода: работоспособна – 1, неработоспособна – 0. Тогда условие работоспособного состояния сложного объекта можно записать Sp = (1,...,1,...,1). Для каждой СЕ условия работоспособности могут
записываться в одном из приведенных выше виде.
Дата добавления: 2015-06-05; просмотров: 769;
