Методы прогнозирования
Имитационное моделирование финансово-хозяйственной деятельности основано на сочетании формализованных (математических) методов и экспертных оценок специалистов и руководителей хозяйствующего субъекта, но с превалированием последних. Поэтому для разработки долгосрочного прогноза со стороны администрации необходимо включить 2—3 специалиста от различных служб и подразделений предприятия (коммерческой службы, планового отдела, финансового отдела и бухгалтерии).
Еще один вариант использования ситуационного анализа для прогнозирования возможных действий имеет более общее применение. Теоретически существуют четыре типа ситуаций, в которых необходимо проводить анализ и принимать управленческие решения, в том челе и на уровне коммерческой организации: в условиях определении, риска, неопределенности, конфликта. Однако с позиции прогнозирования вариантов возможных действий наибольший интерес представляет алгоритмизация действий в условиях риска.
Эта ситуация встречается на практике достаточно часто. Здесь применяется вероятностный подход, предполагающий прогнозирование невозможных исходов и присвоение им вероятностей. При этом пользуется: а) известными типовыми ситуациями (типа — вероятность появления герба при бросании монеты равна 0,5); б) предыдущими распределениями вероятностей (например, из выборочных обследований или статистики предшествующих периодов известна вероятность появления бракованной детали); в) субъективными оценками, сделанными аналитиком самостоятельно либо с привлечением группы экспертов.
Таким образом, последовательность действий аналитика такова:
· прогнозируются возможные исходы Rк, к = 1,2, ..., n; в качестве Ri могут выступать различные показатели, например, доход, прибыль, проиведенная стоимость ожидаемых поступлений и др.;
· каждому исходу присваивается соответствующая вероятность Pк причем
· выбирается критерий (например, максимизация математического ожидания прибыли):
· выбирается вариант, удовлетворяющий выбранному критерию.
Пример
Имеются два объекта инвестирования с одинаковой прогнозной суммой требуемых капитальных вложений. Величина планируемого дохода (тыс. руб.) в каждом случае неопределенна и приведена в виде распределения вероятностей:
| Проект А | Проект В | ||
| Доход | Вероятность | Доход | Вероятность |
| 0,10 | 0,10 | ||
| 0,20 | 0,15 | ||
| 0,40 | 0,30 | ||
| 0,20 | 0,35 | ||
| 0,10 | 0,10 |
Тогда значения математического ожидания дохода для рассматриваемых проектов будут соответственно равны:
E(RA)= 30- 0,10 + 35 -0,20 + 40 -0,40 + 45 -0,20 + 50 • 0,10 = 40 тыс. руб. 44 тыс. руб.
Е (RВ)= 44 тыс. руб.
Таким образом, проект В более предпочтителен. Следует, правда, отметить, что этот проект является и относительно более рисковым, поскольку имеет большую вариацию дохода по сравнению с проектом А.
В данном случае основным критерием отбора варианта была максимизация математического ожидания дохода.
В более сложных ситуациях в анализе используют так называемый метод построения дерева решений. Логику этого метода рассмотрим на простейшем примере.
Пример
Управляющему нужно принять решение о целесообразности приобретения либо станка M1, либо станка М2. Станок М2 более экономичен, что обеспечивает больший доход на единицу продукции, вместе с тем он более дорогой и требует относительно больших накладных расходов (руб.):
| Постоянные расходы | Операционный доход на единицу продукции | |
| Станок Ml | ||
| Станок М2 |
Процесс принятия решения может быть выполнен в несколько этапов.
Этап 1. Определение цели.
В качестве критерия выбирается максимизация математического ожидания прибыли.
Этап 2. Определение набора возможных действий для рассмотрения и анализа (контролируется лицом, принимающим решение).
Управляющий может выбрать один из двух вариантов:
А1= {покупка станка M1)
А2 = {покупка станка М2)
Этап 3. Оценка возможных исходов и их вероятностей (носит случайный характер).
Управляющий оценивает возможные варианты годового спроса на продукцию и соответствующие им вероятности следующим образом:
х1 = 1200 единиц с вероятностью 0,4;
х2 =2000 единиц с вероятностью 0,6;
Р(х1) = 0,4; Р(х2) = 0,6.
Этап 4. Оценка математического ожидания возможного дохода, Выполняется с помощью дерева решений (рис. 2).
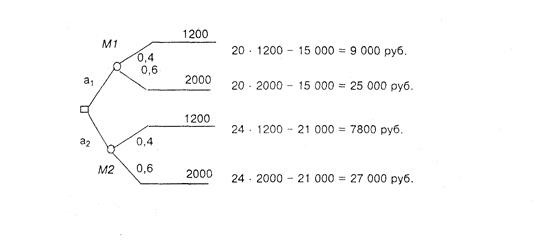
Рис. 2. Дерево решений
Из приведенных на схеме данных можно найти математическое ожидание возможного исхода по каждому проекту:
E(Ra1) = 9000 • 0,4 + 25 000 • 0,6 = 18 600 руб.
E(Ra2) = 7800 • 0,4 + 27 000 • 0,6 = 19 320 руб.
Таким образом, вариант с приобретением станка М2 является экономически более целесообразным.
Мы рассмотрели наиболее общие подходы к формализации процесса прогнозирования возможных действий, основанные на построении дерева решений. Этот метод весьма полезен в различных областях деятельности менеджеров, например, в управленческом учете, при составлении бюджета капиталовложений и особенно анализе на рынке ценных бумаг.
Дата добавления: 2015-06-05; просмотров: 2183;
