Определение длины пути, на котором при увеличении или уменьшении продольного уклона происходит изменение скорости автомобиля от Vi1 до Vi2,, соответствующей новому уклону. 3 страница
Для удобства определения длин кривых и разбивки их на местности имеются специальные таблицы.
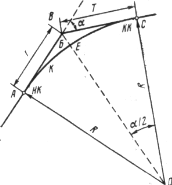
Рис. 5.3. Элементы угла поворота кругового закругления: a – угол; В – вершина угла; А – точка начала круговой кривой (НК); С – точка конца кривой (КК); Б – биссектриса; R – радиус; К – кривая;
Т – тангенс
5.2. Особенности движения автомобиля по кривым
На автомобиль, движущийся по криволинейному участку дороги, в точке кривой, радиус кривизны которой равен R, действует центробежная сила
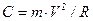 , (5.2)
, (5.2)
где m – масса автомобиля, кг; V – его скорость, м/с.
Центробежная сила, перпендикулярная направлению движения, оказывает на автомобиль опрокидывающее и сдвигающее воздействия. Перераспределяя давление между правыми и левыми колесами, и вызывая явление бокового увода шин, она осложняет также условия управления автомобилем. На кривых малых радиусов увеличивается расход топлива и повышается износ шин. В ночное время проезд криволинейных участков осложняется тем, что свет фар освещает дорогу перед автомобилем на меньшее расстояние, чем на прямых участках. Все указанные отрицательные факторы проявляются тем сильнее, чем меньше радиус кривой в плане. Поэтому безопасность, удобство и экономичность движения автомобилей с расчетной скоростью возможны только при назначении достаточно больших радиусов кривых. В общем виде выражение для определения радиуса круговых кривых в плане может быть получено из следующих соображений.
При движении по кривой на автомобиль действуют две силы, приложенные к его центру тяжести (рис. 5.4): центробежная сила С, направленная во внешнюю сторону закругления и вес автомобиля G. Проектируя обе силы на направление поперечного уклона проезжей части автомобильной дороги, получаем
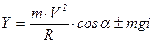 , (5.3)
, (5.3)
где Y – результирующая сила, стремящаяся сдвинуть автомобиль с дороги, называемая поперечной силой.
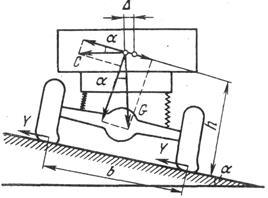
Рис. 5.4. Силы, действующие на автомобиль при движении по кривой в плане
В зависимости от направления поперечного уклона составляющая веса автомобиля, равная mgi, может иметь знак «+» или «– ».
Поскольку угол a мал (cosa=1), его влиянием можно пренебречь. Тогда
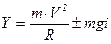 . (5.4)
. (5.4)
Поделив все члены предыдущего уравнения на вес автомобиля, получаем
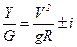 . (5.5)
. (5.5)
Отношение Y/G, обозначаемое m, принято называть коэффициентом поперечной силы. Задаваясь допустимыми значениями коэффициента поперечной силы, можно определить радиус круговых кривых (в м)
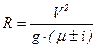 . (5.6)
. (5.6)
Для практического использования этого выражения необходимо нормировать допустимое значение коэффициента поперечной силы.
5.3. Коэффициент поперечной силы
Действующая на автомобиль при проезде по кривой малого радиуса поперечная сила оказывает на него ряд воздействий – стремится сместить его с дороги или опрокинуть, затрудняет управление, снижает комфортабельность поездки, а также, создавая дополнительное сопротивление движению, увеличивает расход топлива и износ шин. С учетом этих воздействий и определяют предельные допустимые значения коэффициента поперечной силы. Устойчивость против заноса является важнейшим условием безопасного движения автомобиля по кривой. Смещению автомобиля вбок под действием центробежной силы и поперечного уклона покрытия препятствует сцепление шин с покрытием. Приложенные к ведущему колесу автомобиля поперечная сила Y и тяговое или тормозное усилие Р создают в плоскости контакта шин с покрытием суммарное сдвигающее усилие Q, направленное под углом к траектории движения (рис. 5.5).
Для устойчивости автомобиля необходимо, чтобы было соблюдено условие
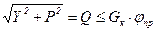 , (5.7)
, (5.7)
где Gк – нагрузка от ведущего или заторможенного колеса на покрытие, Н; jпр – коэффициент продольного сцепления шины с покрытием.
Под воздействием центробежной силы нагрузка между колесами перераспределяется. При большом значении поперечной силы тяговое усилие на менее нагруженном внутреннем колесе может превысить силу сцепления и вызвать буксование колеса и занос автомобиля. Критическим для устойчивости автомобиля является случай интенсивного торможения с блокировкой колеса на кривой, когда работа сил трения шины и дороги почти полностью используется на погашение кинетической энергии поступательного движения автомобиля и лишь малая ее доля остается на сопротивление смещению автомобиля вбок.
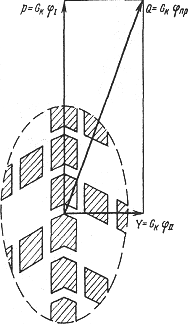
Рис. 5.5. Соотношение между поперечными и продольными усилиями, действующими на колесо автомобиля
Составляющие коэффициента продольного сцепления jпр в продольном jI и поперечном jII направлениях связаны зависимостью
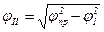 . (5.8)
. (5.8)
Для устойчивости автомобиля на кривой против заноса необходимо, чтобы соблюдалось условие jIIG>Y. Отсюда вытекает требование, чтобы jII>Y/G=m, т.е. коэффициент поперечной силы m не должен превышать остающейся части общего коэффициента сцепления jII, сопротивляющейся смещению шины вбок. Чем большая часть jI общего коэффициента сцепления используется для преодоления продольного уклона при торможении автомобиля, тем меньшая часть его поперечной составляющей jII остается для сопротивления сдвигу автомобиля на кривой.
Практически считается, что используемая часть коэффициента продольного сцепления в продольном направлении jI должна составлять не менее 0,7-0,8 от его полного значения jпр. В этом случае соответственно коэффициент jII равен 0,7 jпр или 0,6 jпр.
Для устойчивости автомобиля при движении по кривой без торможения необходимо, чтобы коэффициент поперечной силы был меньше коэффициента поперечного сцепления m<jпоп.
Устойчивость автомобиля против опрокидывания обеспечивается превышением удерживающего момента над опрокидывающим (см. рис. 5.4).
Составляя уравнение моментов сил, действующих на автомобиль, относительно оси, проходящей через центры площадей контактов внешних колес, получаем
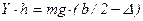 , (5.9)
, (5.9)
откуда
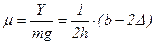 . (5.10)
. (5.10)
В этом выражении учитывается, что из-за деформации рессор и эластичности шин центр тяжести автомобиля смещается в поперечном направлении на некоторую величину D. На основе опытов боковое смещение D можно принять равным примерно 0,2b. Отношение b/h для современных легковых автомобилей колеблется от 1,8 до 2,5, для грузовых – от 2 до 3 и для автобусов – от 1,7 до 2,2, а высоты центра тяжести над поверхностью дороги 0,35-0,6 м для легковых автомобилей, 0,65-1,0 м для грузовых и 0,7-1,4 м для автобусов. Принимая наиболее невыгодные значения h и b/h, получаем, что для устойчивости автомобиля против опрокидывания необходимо, чтобы коэффициент поперечной силы не превышал 0,6.
В нормальных условиях эксплуатации автомобилей и при обычных скоростях движения коэффициент поперечной силы не достигает этого значения. Случаи опрокидывания обычно бывают связаны с наездом колеса автомобиля на препятствие при заносе.
Удобство проезда кривой обеспечивается тем, что действующая на водителя и пассажиров центробежная сила, наклоняющая их вбок, не превысит значения, при котором проезд по кривой становится неприятным.
Данные опытов показывают, что при:
– коэффициенте поперечной силы m=0,10 пассажир, не глядящий на дорогу, не может различить, движется ли автомобиль по кривой или на прямом участке дороги;
– m=0,15 движение по кривой ощущается слабо;
– m=0,20 ясно ощущая движение, пассажир уже испытывает легкое неудобство;
– m=0,30 въезд с прямого участка на кривую ощущается как толчок, наклоняющий пассажира вбок.
Потому считают, что для обеспечения удобства проезда по дороге для пассажиров коэффициент поперечной силы m на кривых не должен превышать 0,15, а в сложных условиях – 0,20.
Экономичность автомобильных перевозок на криволинейных участках связана с возникающим дополнительным сопротивлением движению из-за явления бокового увода шин (рис. 5.6), при котором
– поперечная сила вызывает боковую деформацию шин;
– форма площадки контакта шины с покрытием изменяется, а ее продольная ось образует некоторый угол по отношению к направлению движения (явление бокового увода);
– колесо, оставаясь в той же вертикальной плоскости, начинает смещаться по этому направлению (рис. 5.6б);
– водитель должен компенсировать боковой увод соответствующим поворотом передних колес под углом к движению.
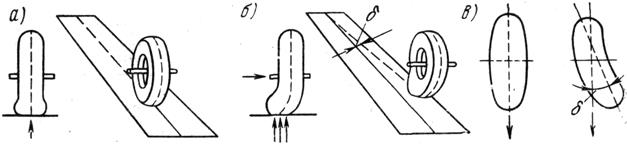
Рис. 5.6. Боковой увод колеса: а – движение при отсутствия боковой силы; б – движение при наличии боковой силы; в – форма площадей контакта шины с покрытием при отсутствии и при наличии боковой силы; d – угол бокового увода
Экспериментальные исследования показали, что при углах бокового увода, меньших 3-4° для шин легковых автомобилей и 4-5° для шин грузовых автомобилей, значение угла пропорционально боковой силе, приложенной перпендикулярно к плоскости качения колеса:
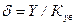 , (5.11)
, (5.11)
где Y – боковая сила, Н; Кув – коэффициент сопротивления уводу, зависящий от упругости пневматической шины в поперечном направлении, для шин легковых автомобилей равен 15-40 Н/рад, для шин грузовых автомобилей – 30-100 Н/рад.
С увеличением угла бокового увода увеличивается затрата мощности двигателя на качение колеса (до 15%) и резко повышается износ шин (до 5 раз). Этим условиям для современных легковых автомобилей соответствует коэффициент поперечной силы, примерно равный 0,1.
Таким образом, чтобы криволинейные участки дорог не являлись причиной существенного повышения себестоимости автомобильных перевозок, необходимо проектировать кривые с радиусами, обеспечивающими при движении автомобилей с расчетной скоростью значения коэффициента поперечной силы, не превышающие 0,1.
5.4. Назначение радиусов кривых в плане
Для безопасности, удобства и экономичности движения с расчетными скоростями следует назначать такие радиусы кривых в плане на автомобильных дорогах, при которых по возможности обеспечивается меньшее значение коэффициента поперечной силы m.
В трудных условиях рельефа или в густонаселенной местности, когда увеличение радиуса ведет к резкому возрастанию объема земляных работ или к необходимости сноса ценных строений, приходится допускать меньшие значения радиусов, безусловно, обеспечивающие устойчивость автомобиля против заноса при движении с расчетной скоростью при благоприятном состоянии дороги, но вызывающие снижение удобства и экономичности пользования дорогой на участке кривой.
Поскольку для обеспечения безопасности движения необходимо, чтобы при проезде автомобиля по кривой имелся определенный запас коэффициента сцепления для экстренного торможения, для погашения поперечной силы можно использовать только часть полного сцепления шины с покрытием. Поэтому расчетное значение коэффициента поперечной силы, назначаемое исходя из комплексного учета требований устойчивости автомобиля, удобства управления, комфортабельности поездок и экономичности перевозок, всегда составляет лишь некоторую часть коэффициента продольного сцепления.
В табл. 5.1 приведены допустимые максимальные значения коэффициента поперечной силы для различных требований устойчивости и использования автомобиля.
Таблица 5.1. Предельные допустимые значения коэффициента поперечной силы
| Показатели | Предельные допустимые значения m на покрытии | ||
| сухом j=0,6 | мокром j=0,4 | покрытом льдом j=0,2 | |
| Устойчивость против опрокидывания | 0,60 | 0,60 | 0,60 |
| Устойчивость против заноса | 0,36 | 0,24 | 0,12 |
| Обеспечение удобства поездки для пассажира | 0,15 | 0,15 | 0,15 |
| Экономичность эксплуатации автомобиля | 0,10 | 0,10 | 0,10 |
Расчетным случаем при назначении радиусов кривых в плане является движение по увлажненному незагрязненному покрытию с коэффициентом продольного сцепления jпр=0,6. При относительно благоприятных условиях местности для расчетов наименьшего радиуса целесообразно ориентироваться на значения m=0,05-0,10, принимая его тем меньшим, чем выше расчетные скорости движения. В СНиП 2.05.02-85 при определении минимальных радиусов принято m=0,12 для расчетных скоростей 150 и 120 км/ч и m=0,18 для скорости 60 км/ч.
Исходя из этих значений коэффициентов, нормы на проектирование автомобильных дорог устанавливают значения допустимых в трудных условиях радиусов кривых в плане в зависимости от скорости движения по дороге (табл. 5.2).
Таблица 5.2. Минимальные радиусы кривых в плане
| Расчетная скорость движения, км/ч | Категория дорог | Наименьшие радиусы на трудных участках дорог, м | |
| в равнинной местности | горной | ||
| I | |||
| II | |||
| III | |||
| IV | |||
| V | |||
| – | |||
| – | |||
| – |
Если дорогу строят в открытой равнинной местности, увеличение радиуса сокращает ее длину и уменьшает строительные и транспортные издержки, Поэтому в благоприятных для проложения трассы условиях рекомендуется на дорогах всех категорий назначать радиусы кривых не менее 3000 м, условия движения по которым практически не отличаются от условий на прямых участках.
На кривых малых радиусов часто не бывает обеспечена безопасность движения с расчетной скоростью в ночное время, поскольку участок дороги, освещенный фарами, оказывается меньше расчетного расстояния видимости. Важность удовлетворения требований безопасности в ночное время подчеркивается тем обстоятельством, что при интенсивности движения ночью примерно в 10 раз меньшей, чем днем, половина дорожно-транспортных происшествий приходится на этот период суток.
Оптические устройства фар концентрируют лучи света в виде эллиптической фигуры, которая может быть охарактеризована углом раствора пучка света фар a, стягивающим в пределах земляного полотна изолинию минимальной допустимой освещенности поверхности дороги, обычно принимаемую равной 2 лк (рис. 5.7).
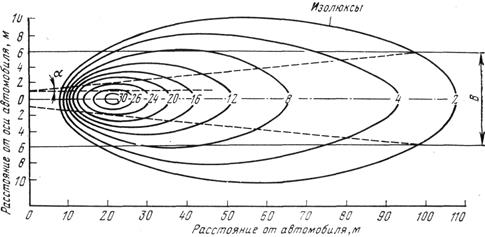
Рис. 5.7. Освещенность дороги светом фар: В – ширина земляного полотна
Современные фары дальнего света в среднем обеспечивают видимость на расстоянии 175 м (максимум 250 м), что меньше расчетных расстояний видимости. Радиус R, при котором видимость дороги на кривой будет соответствовать расчетному значению видимости S, определяется по формуле
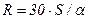 , (5.12)
, (5.12)
где a – угол раствора пучка света (для практических расчетов принимается равным 2°).
Радиус кривых, при которых свет фар освещает проезжую часть на расстояние видимости 100-300 м, составляет 1500-4500 м.
5.5. Переходные кривые
В момент въезда автомобиля с прямого участка на кривую в плане условия движения изменяются. На автомобиль начинает действовать центробежная сила. Теоретически она прилагается мгновенно, практически же – в пределах короткого участка, на котором водитель поворачивает рулевое колесо. Как показали наблюдения, при въезде на кривые с радиусами менее 600 м водители обычно снижают скорость движения. Чтобы изменение условий движения не происходило слишком быстро, между прямым участком и кривой малого радиуса вводят переходную кривую, в пределах которой кривизна оси дороги плавно изменяется от нуля на прямом участке до 1/R в начальной точке круговой кривой.
На автомобильных дорогах I – III категорий автомобили проезжают кривые без снижения скорости. В этих случаях применяют переходные кривые простого очертания. Уравнение A2=RL представляет собой уравнение клотоиды (радиоидальной спирали, радиоиды, спирали Корню) – основной переходной кривой, применяемой на современных автомобильных дорогах.
Минимальная длина переходных кривых устанавливается из условия обеспечения нормируемого значения нарастающего центробежного ускорения J, при котором еще обеспечивается комфортабельное и безопасное движение по дороге
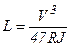 , (5.13)
, (5.13)
где V – расчетная скорость, км/ч; R – радиус закругления, м.
В различных странах значение J принимают в пределах от 0,3 до 1,0 м/с3. Нормы на проектирование дорог Беларуси исходят из значения J=0,8 м/с3, что близко соответствует фактическим режимам движения на дорогах.
Переходные кривые устраивают на дорогах всех категорий на кривых с радиусами менее 2000 м:
радиусы круговых кривых, м 30 60 100 200 300 500 600-1000 1000-2000;
длина переходных кривых, м 30 40 50 70 90 110 120 100.
Приведенные длины переходных кривых следует рассматривать как минимально допустимые. Нормативную длину переходных кривых целесообразно увеличивать в 1,5-2,0 раза, поскольку это придает трассе дороги большую зрительную плавность, способствующую проезду кривой без снижения скорости. При проектировании автомобильных дорог, предназначенных для движения с высокими скоростями, переходные кривые превратились из вспомогательного элемента кривых малых радиусов в самостоятельный элемент трассы дороги в плане и профиле, равноправный с прямыми и кривыми.
Для разбивки переходных кривых иногда применяют уравнения других кривых, также удовлетворяющие требованиям закономерного изменения кривизны. Наибольшее распространение после клотоиды имеют кубическая парабола и лемниската Бернулли.
В ряде западноевропейских стран получили распространение переходные кривые по биквадратной параболе, которые обеспечивают в начале и конце кривой замедленное изменение поперечного ускорения. В отечественной же практике наибольшее распространение получила разбивка переходных кривых по клотоиде (рис. 5.8а), исходные предпосылки о режиме движения автомобилей по которой наиболее логичны.
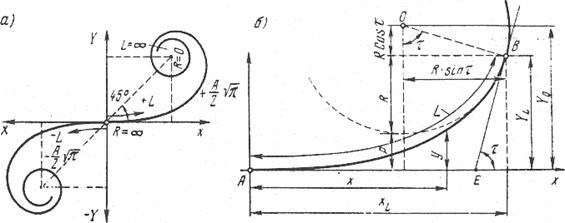
Рис. 5.8. Переходная кривая по клотоиде: а – клотоида; б – сопряжение клотоидой прямолинейного участка трассы с круговой кривой
Так как переходная кривая является частью клотоидной кривой, то ее координаты можно рассчитать по уравнениям клотоиды:
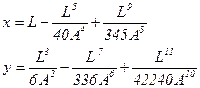 , (5.14)
, (5.14)
где 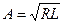 – параметр клотоиды; L – длина участка кривой, соответствующего координатам х и у.
– параметр клотоиды; L – длина участка кривой, соответствующего координатам х и у.
Ряды для х и у быстро сходятся, и при составлении таблиц обычно пользуются двумя первыми членами уравнений (5.14).
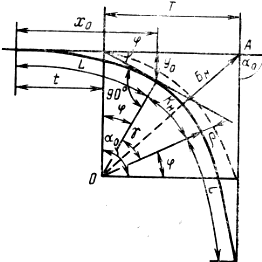
Введение переходных кривых вызывает смещение основной кривой внутрь угла с уменьшением ее длины с BE до CD (рис. 5.9). Это обстоятельство должно учитываться при назначении радиусов кривых, так как для сохранения расчетного значения радиуса R трасса должна быть разбита с радиусом R1=R+p.
Радиус R1=Rcosb+yo, где уо – ордината переходной кривой в точке примыкания к круговой кривой; b =L/2R, рад. Отсюда сдвижка p = R1-R=yo-R(1-cos b). Общая длина тангенса T1=T+t. Остальные параметры закругления с переходными кривыми находятся по формулам (рис. 5.9):
t=xo-Rsinb; Б=(R-p)(sec (a/2)-1); K=2L+K0; K0=p R(a-b)/180; Д=2Т1-К. (5.15)
| 
|
Рис. 5.9. Элементы кругового закругления с переходными кривыми: a – угол; А – вершина угла;
L – длина переходной кривой; р – сдвижка круговой кривой; К0 – длина круговой кривой; Т –тангенс кругового закругления; t –смещение начала закругления после вписывания переходных кривых
Часть основной круговой кривой при этом заменяется переходной кривой. Согласно рис. 5.9 разбивка переходной кривой возможна лишь при условии a³2b. Если это условие не соблюдается, должна быть уменьшена длина переходной кривой или увеличен радиус R.
Практика показывает, что введение переходных кривых становится излишним, если сдвижка меньше 0,2 м.
5.6. Уширение проезжей части на кривых
При повороте автомобиля каждое колесо его движется по самостоятельной траектории, в результате чего ширина занимаемой автомобилем полосы проезжей части увеличивается. Чтобы условия движения по кривой были аналогичны условиям движения на прямом участке, проезжую часть на кривых малых радиусов необходимо уширять (рис. 5.10).
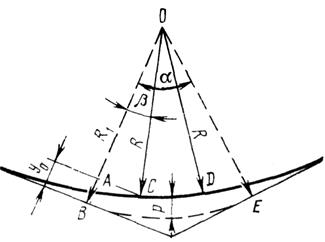
Исходя из допущения, что траектория движения автомобиля в пределах кривой является окружностью, можно получить приближенное выражение для необходимого уширения одной полосы движения на кривой. Из подобия треугольников ABC и BCD находим
АС/ВС = BC/CD, или АС (2R – АС) = l 2. (5.16)
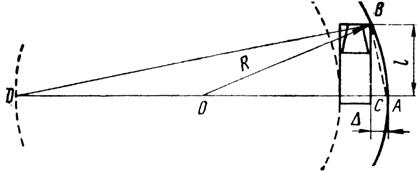
Рис. 5.10. Схема к определению ширины полосы движения на кривой
Пренебрегая в скобках величиной АС, малой по сравнению с 2R, получаем, что необходимое уширение одной полосы движения
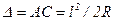 . (5.17)
. (5.17)
Полученная формула уширения на кривой основывается на чисто геометрических соображениях и не учитывает неизбежных отклонений автомобиля при движении от средней траектории. Поэтому она применима только для малых скоростей движения. При больших скоростях уширение одной полосы движения рекомендуется принимать большим, учитывая влияние скорости движения V (в км/ч) и рассчитывать по формуле
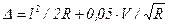 . (5.18)
. (5.18)
Более сложно определение уширения для дорог со значительным движением автопоездов, у которых ширина полосы, занимаемой автопоездом, возрастает с числом прицепов. При обычных сцепных устройствах во время поворота автопоезда вокруг общего центра вращения прицепы смещаются внутрь кривой.
СНиП 2.05.02-85 предусматривает уширение проезжей части дорог с двумя полосами движения на кривых с радиусами менее 1000 м при одновременном ограничении допустимых длин автопоездов. Необходимое уширение проезжей части, составляя при радиусе кривой 1000 м 40 см, при меньших радиусах увеличивается в зависимости от длины расчетных автопоездов до 1,1-3,0 м на кривых радиусом 95 м и до 2,2-3,5 м – на серпантинах.
Проезжую часть уширяют с внутренней стороны кривой за счет обочины. Остающаяся часть обочин должна быть не менее 1,5м на дорогах I и II категорий и 1,0 м – на дорогах остальных категорий. В пределах кривой уширение имеет постоянный размер, а затем постепенно уменьшается на протяжении переходных кривых.
На горных дорогах в виде исключения допускают на кривых малых радиусов частичное размещение уширения на внешней обочине.
5.7. Виражи
Во многих случаях местные условия – рельеф или наличие ценной застройки – не дают возможности разместить кривую расчетного радиуса. Особенно неблагоприятные условия движения создаются для автомобилей, следующих по встречной полосе движения, поскольку составляющая веса, параллельная уклону проезжей части, складывается с соответствующей проекцией центробежной силы. Кроме того, осложняется управление автомобилем в связи с большим, чем для полосы встречного движения, боковым уводом шин. В таких случаях для повышения устойчивости автомобиля и большей уверенности управления на кривых устраивают односкатный поперечный профиль – вираж – с уклоном проезжей части и обочин к центру кривой (рис. 5.11).
Долгое время виражи рассматривали только как дополнительный элемент дороги на кривых малого радиуса, необходимый для безопасности движения автомобилей. Однако опыт эксплуатации автомобильных магистралей показал, что виражи оказывают положительное психологическое воздействие на водителей, способствуя уверенному проезду кривых без неоправданного снижения скорости. При отсутствии виражей скорость на кривых снижается. Поэтому в настоящее время рекомендуется устраивать виражи на кривых в плане с радиусами, меньшими 3000 м на дорогах I категории и 2000 м – на дорогах остальных категорий.
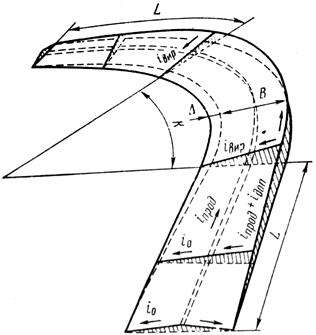
Рис. 5.11. Схема виража на дороге с двухскатной проезжей частью: L – отгон виража и переходная кривая; К – круговая кривая; В – ширина проезжей части; D – уширение проезжей части
Поперечный уклон виража, необходимый для обеспечения скорости движения V (в м/с), при заданном радиусе кривой R может быть определен путем преобразования выражения (5.6)
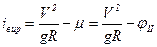 , (5.19)
, (5.19)
где jII – расчетное значение используемой части коэффициента сцепления колеса с дорогой; в данном случае за основной критерий, определяющий коэффициент поперечной силы m принимают устойчивость автомобиля против заноса.
Расчетные значения поперечного уклона на вираже для высоких скоростей движения при малых радиусах кривых могут получаться значительными. Такие виражи устраивают, например, на автодромах, предназначенных для автомобильных гонок.
При проектировании виражей на автомобильных магистралях, рассчитанных на высокие скорости движения, исходят из различных допущений о пропорциональном распределении поперечной силы между сопротивлением шины сдвигу вбок по покрытию и сопротивлением поднятию автомобиля вверх по виражу.
При проектировании виражей на автомобильных магистралях, рассчитанных на высокие скорости движения, исходят из различных допущений о пропорциональном распределении поперечной силы между сопротивлением шины сдвигу вбок по покрытию и сопротивлением поднятию автомобиля вверх по виражу. Обычно считают, что на вираж можно передать 1/3-1/4 действующей на автомобиль центробежной силы.
СНиП 2.05.02-85 предусматривает следующие поперечные уклоны виражей в зависимости от радиусов кривых в плане:
R, м 3000-1000 1000-700 700-650 650-600 < 600;
iв, ‰ 20-30 30-40 40-50 50-60 60.
В районах с частыми туманами и длительными периодами гололеда уклоны виражей не должны превышать 40‰. Лишь в районах с незначительной продолжительностью снегового покрова и редкими случаями гололеда допускается увеличивать поперечный уклон проезжей части на вираже до 100‰. Однако такие крутые виражи неудобны для грузовых автомобилей, движущихся со скоростью, меньшей расчетной.
При поперечном уклоне виража, равном уклону проезжей части на прямом участке, для перехода к односкатному профилю постепенно поворачивают внешнюю половину проезжей части вокруг оси дороги.
При более сложном и в то же время частом случае разбивки виража с уклоном, превышающим уклон проезжей части дороги, для перехода к односкатному профилю производят одновременный поворот внутренней половины поперечного профиля около внутренней кромки покрытия, а внешней – около оси проезжей части. При этом одновременно ось проезжей части смещается внутрь на половину уширения покрытия (рис. 5.12).
Дата добавления: 2015-06-05; просмотров: 4634;
