Определение длины пути, на котором при увеличении или уменьшении продольного уклона происходит изменение скорости автомобиля от Vi1 до Vi2,, соответствующей новому уклону. 1 страница
Если, например, автомобиль въезжает на участок с большим продольным уклоном i2, то из-за избытка силы инерции  , затрачиваемой на преодоление дополнительного подъема, скорость движения изменяется постепенно. При этом отрицательное ускорение при замедлении постепенно уменьшается. Когда оно уменьшится до нуля, дальнейшее движение происходит с постоянной скоростью. Протяженность участка, на котором вновь устанавливается равновесная скорость, можно определить приближенным способом, принимая ускорение в малых интервалах изменения скоростей постоянным. Вначале на основе графика динамических характеристик (рис. 3.14а) строят вспомогательную кривую ускорений, вычитая из значений динамического фактора для Vi2, значения дорожных сопротивлений f+i1 (рис. 3.14б).
, затрачиваемой на преодоление дополнительного подъема, скорость движения изменяется постепенно. При этом отрицательное ускорение при замедлении постепенно уменьшается. Когда оно уменьшится до нуля, дальнейшее движение происходит с постоянной скоростью. Протяженность участка, на котором вновь устанавливается равновесная скорость, можно определить приближенным способом, принимая ускорение в малых интервалах изменения скоростей постоянным. Вначале на основе графика динамических характеристик (рис. 3.14а) строят вспомогательную кривую ускорений, вычитая из значений динамического фактора для Vi2, значения дорожных сопротивлений f+i1 (рис. 3.14б).
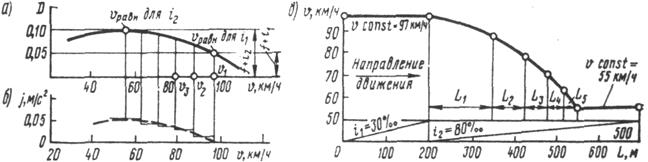
Рис. 3.14. Графическое определение пути, на котором устанавливается равновесная скорость:
а – график динамических характеристик; б – график ускорений; в – построение для определения длины пути изменения скорости
Если обозначить в узком интервале скоростей V1 и V2 (км/ч) среднее значение ускорения через j1, то согласно закономерностям равномерно-замедленного движения расстояние, на котором происходит изменение скоростей
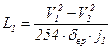 . (3.21)
. (3.21)
Расстояние, на котором происходит изменение скоростей, определится как сумма расстояний L1, L2,..., рассчитанных для всех выделенных интервалов (рис. 3.14в).
Определить, может ли за счет накопленной инерции автомобиль, входящий на подъем со скоростью V1 преодолеть короткий участок дороги длиной L с уклоном imax, превышающим предельный уклон i, найденный по условиям равновесного движения.
В конце подъема скорость должна быть не менее V2. Точнее решение этой задачи для каждого конкретного автомобиля может быть получено по уравнению (3.31). Приближенное решение, пренебрегающее изменением сопротивления воздуха, что направлено в запас надежности расчета, находят из следующих соображений:
1) при постоянной силе тяги двигателя в начале участка сила инерции автомобиля равна  , а в конце участка –
, а в конце участка –  ;
;
2) потеря в живой силе затрачивается на преодоление дополнительного сопротивления движению на подъем (imax – i). Эта работа на пути L составляет LG(imaх – i). Отсюда
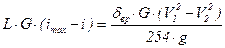 . (3.22)
. (3.22)
Таким образом, длина преодолеваемого по инерции участка с уклоном, превышающим предельный, при равновесной скорости составляет
 , (3.23)
, (3.23)
где V1, V2 – скорости автомобиля, км/ч.
3.6. Особенности движения автомобиля по криволинейному
продольному профилю
На современных автомобильных дорогах участки, имеющие различные продольные уклоны, сопрягают вставкой вертикальных кривых больших радиусов. В условиях пересеченного рельефа местности протяженность вертикальных кривых иногда превышает 50% общей длины дорог высших категорий.
При движении автомобиля по криволинейному продольному профилю преодолеваемый продольный угол непрерывно изменяется, в связи с чем меняется и скорость автомобиля. Это делает условными выводы, вытекающие из рассмотренных выше формул движения с «равновесными скоростями». Поэтому в уравнении движения автомобиля для случая криволинейного продольного профиля сопротивление движению на подъем должно быть принято переменным (рис. 3.15).

Рис. 3.15. Схема к выводу уравнения движения автомобиля по вертикальным кривым
Решения для движения автомобиля по криволинейному продольному профилю были предложены А. Е. Вельским и К. А. Хавкиным. Вертикальные кривые на автомобильных дорогах обычно разбивают по квадратичной параболе
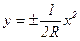 , (3.24)
, (3.24)
аппроксимирующей круговую кривую. Знак «–» относится к выпуклым кривым, знак «+» – к вогнутым.
Если расположить начало координат в начале выпуклой вертикальной кривой в точке О таким образом, чтобы ось х совпадала с хордой вертикальной кривой, то уравнение вертикальной кривой будет иметь вид
 . (3.25)
. (3.25)
Уклон в некоторой точке А на кривой
 , (3.26)
, (3.26)
где a – угол наклона к горизонту хорды, стягивающей вертикальную кривую и являющейся одной из осей координат; 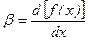 – угол наклона касательной к вертикальной кривой по отношению к хорде (оси х), меняющийся по длине кривой.
– угол наклона касательной к вертикальной кривой по отношению к хорде (оси х), меняющийся по длине кривой.
Согласно рис. 3.15 внешний угол перелома проектной линии w=i1+i2, угол наклона хорды к горизонтали
 . (3.27)
. (3.27)
Углы a, b и w должны быть выражены в радианах.
Подставляя найденное значение a в уравнение (3.26), получаем, что уклон в точке А
 . (3.28)
. (3.28)
При выводе этой формулы в связи с малыми значениями продольных уклонов, допускаемых на автомобильных дорогах, пренебрегали разностью в длинах, измеряемых для одной и той же точки по хорде и ее горизонтальной проекции.
Правые части кривых на графиках динамических характеристик за точкой максимума могут быть выражены уравнением вида
 , (3.29)
, (3.29)
где G – вес автомобиля, Н; V – скорость автомобиля, м/с; а, b – параметры, характеризующие зависимость силы тяги от скорости движения на разных передачах и при разной степени открытия дроссельной заслонки.
Параметры а и b определяют подбором по графикам кривых динамических характеристик. Их можно получить и расчетом исходя из уравнения внешней характеристики двигателя. Значения параметров а, b и m для случая движения некоторых автомобилей на прямой передаче при полном открытии дроссельной заслонки и при полной нагрузке автомобиля приведены в табл. 3.6.
Таблица 3.6. Значения параметров а, b и m
| Автомобиль | а, Н | b, Н×с2/м2 | m, 1/м |
| ЗИЛ-114 | 1,94 | 4,9×10-4 | |
| ГАЗ-24 «Волга» | 0,8 | 4,1×10-4 | |
| ВАЗ-2101 | 0,45 | 3,1×10-4 | |
| «Москвич-412» | 1,9 | 3,2×10-4 | |
| ЗИЛ-130 | 4,5 | 3,0×10-4 | |
| КамАЗ-5320 | 3,1 | 4,0×10-4 |
Подставляя в основное уравнение динамического фактора автомобиля (3.18) значения переменного продольного уклона и уравнение динамической характеристики (3.29), получаем исходное дифференциальное уравнение для определения скоростей движения по выпуклому криволинейному продольному профилю
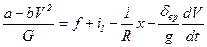 . (3.30)
. (3.30)
Решение дифференциального уравнения с учетом того, что  , а также с учетом начального условия, что при x=0 скорость Vx равна начальной скорости Vн (в м/с), развитой в конце предшествующего участка, приводит к выражению
, а также с учетом начального условия, что при x=0 скорость Vx равна начальной скорости Vн (в м/с), развитой в конце предшествующего участка, приводит к выражению
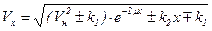 , (3.31)
, (3.31)
где 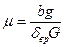 (см. табл. 3.4); е – основание натурального логарифма; k1 и k2 – коэффициенты, определяемые по формулам
(см. табл. 3.4); е – основание натурального логарифма; k1 и k2 – коэффициенты, определяемые по формулам  ,
, 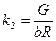 .
.
Для выпуклых кривых в формуле (3.31) следует принимать верхние знаки, для вогнутых кривых – нижние. Начальный продольный уклон i принимают для подъемов со знаком «+», для спусков – со знаком «–».
Поскольку в выражения (3.29), (3.30) и (3.31) входит вес автомобиля G, уравнение (3.31) может быть использовано для расчетов скоростей движения автопоездов и автомобилей при разной степени загрузки.
3.7. Торможение автомобиля
Нормальный эксплуатационный режим торможения соответствует неполной блокировке колес, при которой колесо катится по покрытию с небольшим пробуксовыванием. Такой режим торможения наиболее эффективен. Однако при аварийной ситуации и срочном торможении водитель не имеет возможности регулировать интенсивность нажатия тормозной педали и выжимает ее полностью. Торможение проходит при пониженных коэффициентах сцепления, которые и определяют при экспериментах.
Для характеристики интенсивности замедления автомобиля при торможении с выключенным сцеплением, когда силой, движущей автомобиль, является его инерция, может быть использовано уравнение движения автомобиля в следующем виде:
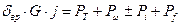 , (3.32)
, (3.32)
где Рw, Pi, Pf – силы сопротивления движению; PТ=gТG – тормозная сила; G – вес автомобиля; gТ – коэффициент тормозной силы (интенсивности торможения), равный отношению суммы тормозных сил, возникающих на всех тормозных колесах, к весу автомобиля.
Параметр gТ зависит от конструктивных особенностей тормозной системы автомобиля и ее состояния, а также от интенсивности торможения водителем. На значение параметра gТ оказывает влияние также ровность проезжей части, так как при движении по покрытию, имеющему неровности, возникают колебания автомобиля, при которых в отдельные моменты рессоры разжимаются, уменьшая давление автомобиля на дорогу.
Подставляя в уравнение (3.32) значения сопротивлений движению, получаем отрицательное ускорение при торможении, характеризующее интенсивность замедления автомобиля
 . (3.33)
. (3.33)
Длина пути, на котором водитель может остановить автомобиль, движущийся с расчетной скоростью, – тормозной путь – важная характеристика безопасности движения.
При расчетах тормозного пути для определения элементов плана и профиля автомобильных дорог условно принимают суммарное время t1+t2+t3 (время реакции + время холостого хода педали тормоза + время нарастания тормозного усилия) равным 1 с, называя его временем реакции водителя. Оно приблизительно соответствует большой сосредоточенности внимания водителя при управлении автомобилем.
Путь, проходимый автомобилем за период полного торможения, можно рассчитать по формуле равномерно замедленного движения
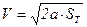 , (3.34)
, (3.34)
где V – скорость в начале торможения, м/с; ST – тормозной путь, м; а – абсолютное значение отрицательного ускорения (замедления) при торможении, м/с2, равное (gТ+f±i)g. При этом допускают, что сопротивление воздуха отсутствует, пренебрегают влиянием вращающихся масс автомобиля.
По действующим требованиям к тормозным механизмам автомобилей абсолютное значение замедления а должно составлять для грузовых автомобилей и автопоездов 5,5 м/с2, для легковых автомобилей – 7 м/с2.
Подставляя значение а в уравнение (3.34), получаем выражение для тормозного пути
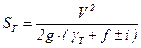 . (3.35)
. (3.35)
При расчетах, связанных с определением геометрических элементов плана и продольного профиля дорог, исходят из наиболее опасного случая – аварийного режима торможения с полной блокировкой колес, принимая gТ равным коэффициенту сцепления jпр. Однако в реальных условиях эксплуатации автомобилей из-за неточной регулировки тормозов, неравномерности распределения усилия между колесами и колебаний автомобиля при движении в процессе торможения не удается реализовать теоретически возможную полную величину тормозной силы. Это учитывается введением в формулу тормозного пути поправочного коэффициента эффективности торможения Кэ. Поэтому расчетное значение тормозного пути
 . (3.36)
. (3.36)
По данным опытов для легковых автомобилей следует принимать Кэ=1,2, а для грузовых автомобилей и автобусов Кэ=1,3-1,4. При торможении на скользких покрытиях на всех колесах тормозные усилия достигают максимально возможного значения практически мгновенно. Поэтому при коэффициентах сцепления jпр£0,4 можно считать Кэ=1. При расчетах геометрических элементов автомобильных дорог принимают среднее значение Кэ=1,2.
Уравнение (3.36) дает заниженные результаты при расчетах для скоростей движения, превышающих 90–100 км/ч, поскольку оно не учитывает особенностей поведения водителя, тормозящего при высоких скоростях. Из-за опасности заноса торможение ведется вначале при легком нажиме на педаль без полного использования возможности тормозов и лишь со скорости 70–80 км/ч начинается интенсивное торможение. В этом случае Кэ=2,3. На это значение следует ориентироваться при обосновании требований к геометрическим элементам автомобильных магистралей.
При расчетах элементов дорог для обеспечения большей безопасности движения за расчетный тормозной путь принимают путь, проходимый за период реакции водителя l1, путь, проходимый автомобилем за период полного торможения l2, и зазор безопасности между остановившимся автомобилем и препятствием l3, обычно принимаемый равным длине автомобиля (рис. 3.16). В этом случае при скорости V (в км/ч) формула для Sрасч (в м) принимает вид
 . (3.37)
. (3.37)

Рис. 3.16. Схема к определению тормозного пути: Sрасч – расчетный тормозной путь; l1 – путь, проходимый за время реакции водителя; l2 – путь торможения; l3 – расстояние безопасности
При расчете скорости движения под уклон по графику динамических характеристик сопротивление от уклона входит в уравнение с отрицательным знаком
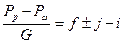 . (3.38)
. (3.38)
На крутых спусках ускорение приобретает большое значение, происходит разгон автомобиля и быстрое возрастание его скорости. Движение автомобиля под уклон с большими скоростями, особенно при неровном или скользком покрытии и наличии кривых в плане, очень опасно. Управление автомобилем затрудняется. Поэтому водители в зависимости от крутизны спуска принимают специальные меры снижения скорости – уменьшают подачу рабочей смеси в двигатель, периодически притормаживают, не выключая сцепления, или переходят на совместное торможение одновременно тормозами и двигателем, включая одну из понижающих передач.
Торможение автомобилей на спусках, особенно длинных, с использованием колесных тормозов нерационально, так как при длительном торможении коэффициент трения фрикционных накладок резко уменьшается из-за нагревания тормозных барабанов. Это снижает эффективность торможения и приводит к быстрому износу тормозов. Торможение двигателем осуществляется уменьшением подачи топлива при отпускании педали дроссельной заслонки. Однако снижению числа оборотов двигателя до частоты вращения на холостом ходу препятствует принудительное вращение коленчатого вала через механизм трансмиссии ведущими колесами со скоростью, соответствующей скорости автомобиля. В результате этого дополнительно появляется сила сопротивления РТД, увеличивающая сопротивление движению. Значение РТД на ведущих колесах при полностью закрытой дроссельной заслонке и при движении на прямой передаче для легковых автомобилей может быть найдено по эмпирической формуле
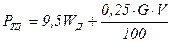 , (3.39)
, (3.39)
где WД – рабочий объем двигателя, л; V – скорость, км/ч; G – вес автомобиля, Н.
Движущей автомобиль силой является параллельная уклону дороги составляющая его веса, силами сопротивления движению являются тормозная сила двигателя и силы сопротивлений воздуха и качению автомобиля.
Равновесная скорость, которая устанавливается при торможении двигателем, может быть рассчитана теоретически на основе общей формулы уравнения движения (3.17) и определится как 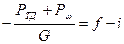 .
.
Эффект торможения двигателем проявляется особенно сильно при включении понижающих передач, обусловливающих при той же скорости автомобиля более быстрое вращение вала двигателя. Для расчетов, соответствующих этому случаю, в уравнении (3.39) вместо V подставляют величину V×iк, где iк – передаточное число включенной передачи.
На избираемый водителями режим движения на спусках большое влияние оказывают особенности восприятия ими условий движения – длина спуска, продольный уклон, ясность дорожных условий в конце спуска.
Наблюдения показывают, что на спусках чаще всего используются следующие режимы движения:
– при уклоне i £ 20‰ – движение с тяговым усилием на ведущих колесах независимо от протяженности спуска;
– при 30‰ <i < 50‰ – движение с выключенным сцеплением на участках длиной соответственно до 500-300 м, торможение двигателем в нижней части для грузовых автомобилей;
– при i > 60‰ – торможение двигателем; при длине спуска менее 1000 м совместное торможение двигателем и колесными тормозами.
3.8. Особенности тяговых расчетов автопоездов
В равных дорожных условиях производительность автопоезда в 1,5-2,0 раза выше, чем у автомобиля-тягача без прицепов. Чтобы обеспечить эффективное использование автопоездов, дороги должны удовлетворять более высоким требованиям, чем в случае движения одиночных автомобилей.
Динамический фактор автопоезда меньше, чем одиночного автомобиля, поскольку при большей общей массе сила тяги остается такой же. В то же время сопротивление движению у автопоезда выше. Из-за трения в сцепных приборах и поворотном круге, а также из-за раскачиваний прицепов на ходу, сопротивление качению у автопоезда возрастает с увеличением количества прицепов. Увеличивается также и сопротивление воздуха, так как каждый дополнительный прицеп добавляет трение воздуха о боковую поверхность и завихрение воздушных струй за собой.
Уравнение динамического фактора для автопоезда имеет вид
 , (3.40)
, (3.40)
где Рwап – сопротивление воздуха движению автопоездов; Ga – вес автомобиля; Gпр – вес прицепов; f1 – коэффициент сопротивления качению для автопоездов; dап – коэффициент учета вращающихся масс автопоезда.
Для практических расчетов можно принять, что коэффициент обтекаемости возрастает от каждого прицепа на 25-30%, для полуприцепа – на 10%, а коэффициент сопротивления качению – на 4-5%.
Еще более неблагоприятные результаты дает проверка на обеспеченность сцепления ведущих колес с покрытием при трогании с места. В этом случае при отсутствии сопротивления воздуха уравнение движения автопоезда имеет вид
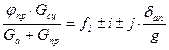 . (3.41)
. (3.41)
Проф. Я. X. Закин предлагает также учитывать при расчетах на трогание автопоездов с места возникающие дополнительные сопротивления, увеличивая коэффициент сопротивления качению для летних условий в 1,5-2,5 раза, для зимних – в 2,5-5 раз.
Для повышения безопасности движения современные автомобильные прицепы снабжаются тормозами, управляемыми с автомобиля, что и определяет общий вид уравнения движения автопоезда при торможении
 , (3.42)
, (3.42)
где PТ – нагрузка на тормозные оси.
Путь, проходимый заторможенным автопоездом, превышает путь одиночного автомобиля. Интенсивность торможения при остановке автопоездов ниже, чем одиночных автомобилей, так как резкое торможение автопоезда вызывает опасность заноса прицепов или наезда их на автомобиль.
Из изложенного следует, что при проектировании дорог, по которым предполагается интенсивное движение автомобильных поездов, нецелесообразно применять большие продольные уклоны. Желательно, чтобы независимо от категории дорог они не превышали 30-40‰, а при невозможности этого на участках подъемов должны быть предусмотрены дополнительные полосы проезжей части.
3.9. Расход топлива и износ шин в зависимости от дорожных условий
Расход топлива при автомобильных перевозках зависит от дорожных условий и режимов движения.
Для оценки расхода топлива при сравнении вариантов автомобильных дорог может служить график экономической характеристики автомобиля, указывающий расход топлива в литрах на 100 км пробега при разных сопротивлениях дороги и скоростях движения (рис. 3.17).

Рис. 3.17. Пример графиков экономической характеристики: I – III – группы кривых, относящихся к случаям движения на I –III передачах; 1 – кривые максимальных расходов топлива при движении с разными скоростями (цифры на кривых характеризуют дорожные сопротивления y=f+i)
График экономической характеристики строят для разных передач в виде семейства кривых, каждая из которых относится к определенному значению суммы дорожных сопротивлений – сопротивления движению и сопротивления движению на подъем (y=f+i). Огибающие семейства кривых для каждой передачи соответствуют полному открытию дроссельной заслонки. Экономические характеристики автомобилей могут быть получены расчетным путем и сняты экспериментально.
Расход топлива при построении графика экономических характеристик принято выражать в литрах на 100 км пути, который возможно рассчитать по формуле
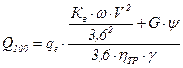 , (3.44)
, (3.44)
где qе – удельный расход топлива, г/(кВт×ч); Кв – коэффициент сопротивления воздуха; hТР – КПД трансмиссии автомобиля; g – плотность топлива, г/см3.
От скорости автомобиля на отдельных участках зависит также износ шин. Высокие скорости движения значительно повышают износ шин (рис. 3.18). Это вызывается значительным нагреванием шин, а также увеличением силы ударов о неровности дорожной одежды. Износ шин зависит также от типа покрытия.
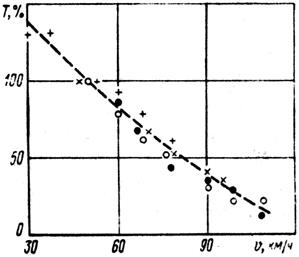
Рис. 3.18. Зависимость износа шин от скорости движения: Т – относительный срок службы шин, %. Различные условные знаки относятся к данным разных авторов
Если принять пробег шин на дорогах с ровным твердым усовершенствованным покрытием за 100%, то на дорогах с менее ровными покрытиями (щебеночные, гравийные, булыжная мостовая) он снижается на 25-30%, а на дорогах с покрытиями с большим количеством деформаций – на 50%.
4. ОСНОВЫ ТЕОРИИ ТРАНСПОРТНЫХ ПОТОКОВ
4.1. Характеристики режимов движения потоков автомобилей
Следуя из разных мест отправления в разные места назначения, автомобили образуют на дороге транспортные потоки, движущиеся навстречу друг другу. В каждом транспортном потоке осуществляется взаимодействие автомобилей. Поэтому все проектные решения, принимаемые на основе нормативов, разработанных применительно к движению одиночного автомобиля, должны анализироваться с точки зрения удовлетворения ими требований движения транспортных потоков.
Загрузка дороги движением оказывает непосредственное влияние на:
1) степень удобства проезда по дороге;
2) легкость управления автомобилем;
3) эффективность использования автомобильного транспорта;
4) расход топлива.
В зависимости от степени загрузки дороги автомобилями различают несколько характерных режимов транспортных потоков, связывая с ними понятие об уровнях удобства движения:
1) свободный поток (уровень удобства движения А, рис. 4.1а) – одиночные автомобили, едущие по дороге на таком расстоянии друг за другом, что они не оказывают взаимного влияния на условия движения (более 100 м);
2) частично связанный поток (уровень удобства движения Б, рис. 4.1б) – движение происходит в виде групп, состоящих из нескольких автомобилей, которые отличаются по динамическим качествам и следуют на близком расстоянии друг за другом (50-100 м). Обычно это вызывается тем, что передний автомобиль, движущийся более медленно, задерживает задние. Водители их вынуждены ехать медленнее, чем хотели бы, ожидая удобного момента для совершения обгона с выездом на соседнюю полосу, после чего получают возможность продолжать движение с режимом одиночного автомобиля, пока не нагонят следующую группу. Средние скорости потока снижаются, управление автомобилем осложняется;
3) связанный поток (уровень удобства движения В, рис. 4.1в) – движение происходит в виде больших групп автомобилей (20-50 м). Все автомобили оказывают взаимное влияние и сразу после обгона одиночного автомобиля или группы скорость автомобиля начинает вновь определяться движением едущего перед ним автомобиля. Обгоны осуществляются с тем большей трудностью и риском, чем выше интенсивность движения. Комфортабельность поездок существенно ухудшается. От водителей требуется повышенная внимательность;
4) плотный, или насыщенный, поток (уровень удобства движения Г, рис. 4.1г) – автомобили следуют друг за другом (менее 20 м). Обгоны становятся практически невозможными. Скорость движения резко снижается. В местах ухудшения дорожных условий возможно возникновение заторов.
Поскольку условия движения автомобилей для каждого из указанных режимов различны, они описываются различными закономерностями теории транспортных потоков. При этом в связи с колебаниями интенсивности движения в разные дни и часы суток на одном и том же участке дороги режимы движения изменяются.
Движение по дороге потока автомобилей представляет собой своеобразный неустановившийся процесс, в котором взаимное расположение и скорости автомобилей все время меняются случайным образом. Поэтому режим движения потока может быть охарактеризован только средними статистическими показателями.
Измерения на каком-либо участке дороги скоростей движения автомобилей показывают, что они меняются в сравнительно широком интервале, но для основной массы автомобилей располагаются вблизи некоторого среднего значения. Чем плотнее транспортный поток, тем меньше в нем различие в скоростях отдельных автомобилей. При интенсивности движения, соответствующей частично связанному транспортному потоку, кривые распределения числа автомобилей по скорости движения (рис. 4.2а) имеют колоколообразное очертание, характерное для нормальной кривой распределения.


Рис. 4.1. Движение по дороге при разной насыщенности транспортного потока
Скорости и режимы движения транспортных потоков характеризуют также кумулятивными кривыми, показывающими, какой процент из общего количества автомобилей движется со скоростями, меньшими заданной (рис. 4.2б):
1) средняя часть кривой соответствует основной части потока;
2) нижняя часть кривой примерно до 15% обеспеченности показывает, с какой скоростью движутся наиболее медленные автомобили, вызывающие основную потребность в обгонах;
Дата добавления: 2015-06-05; просмотров: 3744;
