Корневые оценки качества

Корневые критерии качества основываются на исследовании расположения корней характеристического уравнения замкнутой системы, то есть полюсов передаточной функции системы, а также и нулей этой передаточной функции.

Вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая ограничения на корни характеристического уравнения.

Для оценки быстродействия системы используется понятие степени устойчивости, являющейся простейшей корневой оценкой качества.

Под степенью устойчивости a понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.6.5).

Если ближайшим является вещественный корень, то такая степень устойчивости называется апериодической, так как ей соответствует апериодическая составляющая переходного процесса с₁e^-at. Время ее затухания характеризует общую длительность переходного процесса, так как все члены решения, соответствующие остальным корням, затухают быстрее, т.е.

t_p @ 3/a. (6.25)

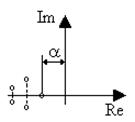
Рис. 6.5. Комплексная плоскость корней

Если ближайшем к мнимой оси окажется пара комплексных корней, то ей соответствует колебательная составляющая переходного процесса с₁e^-atsin(bt+b₁), при этом оценка длительности переходного процесса остается прежней. Такая степень устойчивости называется колебательной.

Для оценки запаса устойчивости системы введено понятие колебательности переходного процесса.

Колебательность определяется величиной

m = ç 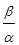ç, (6.26)

где a и b - вещественная и мнимая части корней характеристического уравнения. Именно эта величина характеризует быстроту затухания колебаний за каждый период T=2p/b. Чем выше колебательность, тем слабее затухание колебаний в переходном процессе.

Суммарное требование определенных значений степени устойчивости a и колебательности m приводит к области, изображенной на рис.6.6, внутри которой должны располагаться все корни характеристического уравнения замкнутой системы.

Далее необходимо иметь в виду, что для определения качества переходного процесса при единичном скачке задающего воздействия существенны не только корни характеристического уравнения, т.е. полюса, но также и нули передаточной функции замкнутой системы.

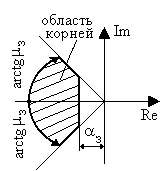
Рис. 6.6. Область расположения корней:

где a_з и m_з - заданные значения степени устойчивости и колебательности

Для уменьшения амплитуд отклонений выходной величины системы в переходном процессе желательно, чтобы нули передаточной функции замкнутой системы располагались вблизи ее полюсов.

Примером корневых оценок качества переходного процесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876 г., положившей начало развития теории управления) [1,2].

Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. При выборе расположения полюсов и нулей передаточной функции необходимо придерживаться общих рекомендаций [1].

1. Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе.

2. Для уменьшения отклонений в переходном процессе выгодно удалять полюсы друг от друга.

3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси.

Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованием обеспечения определенного запаса устойчивости и быстродействия.