Розподіл Фермі-Дірака та розподіл Бозе-Ейнштейна.

Бозони – частинки з цілим або або нульовим спіном (можуть знаходитись в межах даної системи в однаковому стані і в обмеженій кількості).

Ферміони-частинки з напіцілим спіном. Розглянемо систему: ідеальний газ з 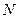частинок, тоді :

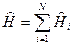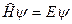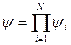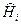, , - для системи з однакових частинок, -хв ф 1-ї част, -гам 1-част.

Р-ння Шр. для системи- зводиться до рівняння для однієї част 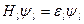; набір кв чисел, що визн.стан системи. Тоді енергія системи 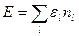; 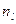-число част в -му стані. 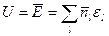, 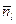- середнє число част., що знаходяться в -стані. Нехай 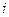-номер енергетичного рівня; 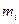-кратність його виродження ( число станів на 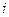-му рівні, що мають одне значення енергії ), тоді ; позначимо 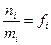-середнє число частинок в одному стані. Це фактично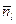

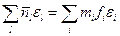
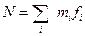-повне число частинок. Наша система ізольована і знаходиться в рівноважному стані. В ньому 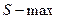і за принципом Больцмана: 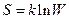, 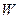-число мікростанів, які відповідають даному макростану. На одному рівні 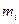місць. Розміщення по них частинок:

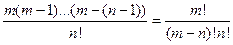; тоді 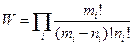- для Ферміонів (в 1-стані -1 частинка)

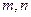-великі, тоді за формулою Стірлінга: :

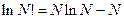Вимагаємо max ентропії, будуємо функціонал Лагранжа: 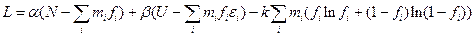вимагаємо 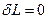: 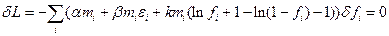; 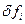-довільні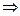 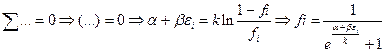, - невідомі. 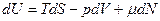, , 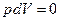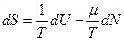. З іншого боку :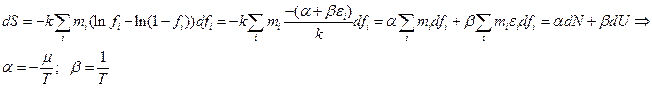

отже 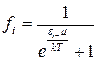- функція розподілу Фермі-Дірака: імовірність, що стан 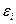-зайнятий, або середня к-ть частинок в стані з енергією 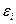. Квантові результати переходять в класичні при умові 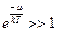- умова стат.невиродження. Розподіл Бозе- Ейнштейна: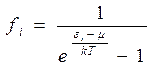

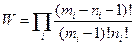( - перетворення аналогічні,

)

,

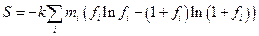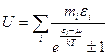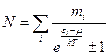
суми беруться по енергетичним рівням.