Висновок канонічного розподілу
1 Розглянута система X разом з термостатом Y представляє собою велику гамільтонових систем, що знаходиться в стані термодинамічної рівноваги. Останнє означає, що всі середні значення фізичних величин не змінюються з часом. Це означає, що щільність ймовірності (в квантовому випадку - відповідний оператор) не залежить від часу:
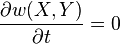
отже, рівноважна щільність верятності є інтегралом руху, тобто деякою функцією механічних інтегралів руху, в т.ч. гамільтоніана. Оскільки в розглянутих системах імпульси і моменти імпульсів не є інтегралами руху, то фактично щільність ймовірності може бути функцією лише гамільтоніана і можливо інших (неадитивні) інтегралів руху. Однак, виходячи з постулату транзитивності теплової рівноваги можна показати, що будь-які характеристики термодинамічної системи залежать лише від енергії і зовнішніх параметрів. Отже, щільність ймовірностей повинна бути лише функцією гамільтоніана
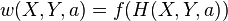
Гамільтоніан великої системи можна представити як суму гамільтоніаном розглянутої системи і термостата, нехтуючи гамільтоніаном взаємодії
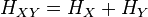
Оскільки
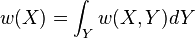
Отже, можна вважати, що щільність ймовірності даної системи залежить тільки від її гамільтоніана
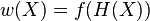
2 Для виведення конкретної форми залежності розглянемо дві невзаємодіючі між собою системи, що знаходяться в рівновазі з термостатом. Ці системи можна з достатньою точністю вважати незалежними з урахуванням того, що їх розмір істотно малий у порівнянні з термостатом і опосередкований взаємозв'язок через термостат (через закон збереження енергії) слабка. Отже
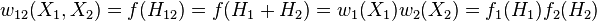
Тобто 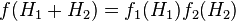
Логаріфміруя даний вираз отримаємо 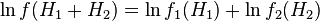
Диференціал дорівнює 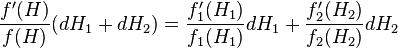
У зв'язку з довільністю гамільтоніаном це співвідношення можливо тільки якщо коефіцієнти при диференціалів однакові і постійні
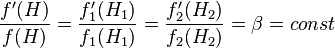
Звідси отримуємо канонічне розподіл Гіббса 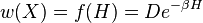
Дата добавления: 2015-06-01; просмотров: 947;
