Оператори координати, імпульсу, енергії.

Оператор - це математичний символ для позначення дії або програм дій, які потрібно здійснити над деякоюфункцією, щоб однозначно отримати іншу функцію.

В квантовій механіці оператори діють на хвильову функцію, яка є комплекснозначних функцій, що дає найбільш повний опис стану системи, і позначаються великими латинськими літерами з циркумфлекс нагорі. Наприклад:

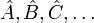
Оператор діє на функцію, яка стоїть праворуч від нього (кажуть також, що він застосовується до функції або множиться на функцію):

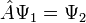
У квантовій механіці використовується математичне властивість лінійних самосопряженних (ермітових) операторів, що полягає в тому, що кожен з них має власні вектори і власні речові значення. Вони виступають у ролі відповідних даному оператору значень фізичних величин.

1. Арифметичні операції над операторами

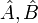Оператор називається сумою (різницею) операторів , Якщо для будь-якої функції 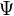з області визначення всіх трьох операторів виконана умова:

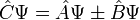
Оператор називається твором операторів 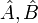, Якщо для будь-якої функції 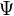виконана умова:

У загальному випадку

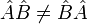
Якщо , То кажуть, що оператори 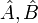коммутіруют. Комутатор операторів визначається як

2. Власні значення і власні функції оператора

Якщо має місце рівність:

то 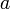називають власним значенням оператора 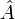, А функцію 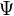- Власної функцією оператора 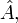відповідної даному власному значенню. Найчастіше в оператора є безліч власних значень: Безліч всіх власних значень називається спектром оператора.

3. Лінійні та самосопряженних операторів

Оператор 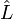називається лінійним, якщо для будь-якої пари 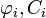виконана умова:

Оператор 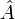називається самосопряженним ( ермітових), якщо для будь-яких 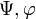виконана умова:

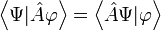
При цьому сума самосопряженних операторів є самосопряженних операторів. Твір самосопряженних операторів є самосопряженних операторів, якщо вони комутують. Власні значення самосопряженних операторів завжди речовинні. Власні функції самосопряженних операторів, що відповідають різним власним значенням, ортогональні.

4. Оператори, що використовуються в квантовій фізиці

Основними характеристиками фізичної системи в квантовій фізиці є спостережувані величини і стану.

В квантовій фізиці спостережуваним величинам зіставляються лінійні самосопряженних операторів вкомплексному сепарабельному гільбертовому просторі, станам - класи нормованих елементів цього простору (з нормою 1). Це робиться в основному з двох причин:

Власні значення самосопряженних операторів, що відповідають конкретним значенням фізичних величин, є речовими числами, тобто тим, з чим на практиці мають справу експериментатори (показання приладів, результати обчислень і т. д.).

Одна і та ж квантова частинка може перебувати одночасно у безлічі квантових станів, які і характеризуються безліччю власних значень відповідного оператора. Це може бути кінцеве безліч(дискретний спектр значень), інтервал (безперервний спектр значень) або змішане безліч.

В квантовій фізиці існує "нестроге" правило для побудови оператора фізичних величин: співвідношення між операторами в цілому таке ж, як між відповідними класичними величинами. Грунтуючись на цьому правилі, були введені наступні оператори (в координатному представленні):

Оператор координат :

Дія оператора координат полягає в множенні на вектор координат.

Оператор імпульсу :

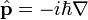Тут 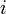- уявна одиниця, - оператор Набла.

Оператор кінетичної енергії :

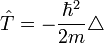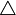Тут - постійна Планка, - оператор Лапласа.

Оператор потенційної енергії :

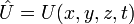
Дія оператора тут зводиться до множення на функцію.

Оператор Гамільтона :

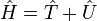
Оператор моменту імпульсу :

Оператор спина :

У найважливішому випадку спина 1/2 оператор спина має вигляд:

, Де , , 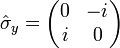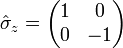- Т.зв. матриці Паулі.