Сложность систем

Понятие сложности применительно к техническим системам имеет не только философско-методологическое значение, но и определенную практическую ценность. В логико-философской литературе предпринимаются многочисленные попытки уточнения этого понятия. Нам представляется >обобщающим подход к понятию критерия сложности (простоты) применительно, например, к проектированию летательных аппаратов с позиций общей теории систем (ОТС).

В работах Уемова дан анализ существующих взглядов на определение сложности систем с позиций параметрической теории систем. Автор выделяет несколько видов сложности: унарную, характеризующую в отдельности концепт Р, структуру или субстрат системы; бинарную, характеризующую сложность любого компонента системы Р, R и m,соотнесенного к любому другому компоненту, включая самого себя; и интегральную, оценивающую сложность системы в целом (соотнесенность всех компонентов системы). Здесь параметры P, R,m соответствуют формуле (4.1).

Мерой сложности системы в ОТС принята энтропия, подобно тому, как в теории информации она выступает мерой количества информации, а в термодинамике - мерой необратимости процесса преобразования тепловой энергии в механическую. Субстратная сложность в данном случае, характеризуя систему, выступает в роли величины энтропии как меры нео­пределенности знаний о системах, которые выбираются нами при построении аппарата. При оценке вариантов летательных аппаратов принимаем, что все подсистемы (блоки, агрегаты, узлы), которые входят в состав изделия, имеют одинаковую степень изученности, т. е. их энтропия одинакова.

С точки зрения оценки простоты или сложности вариантов построения летательного аппарата, конкретного технического устройства с набором заранее известных подсистем, которые рассматриваются как альтернативные при синтезе аппарата, наиболее существенными типами сложности (простоты) будут структурная, структурно-субстратная и субстратно-структурная.

Энтропия в соответствии с формулой К. Э. Шеннона определятся в виде

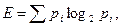(13.1)

где в теории информация p_i – вероятность каждого из воз­можных сообщений при конечном множестве символов.

Состояние объекта и его свойства характеризуются значениями параметров его составляющих элементов и их взаимоотношениями. На всех этапах разработки сложных технических устройств необходимо находить эти связи, устанавливать степень их знания, сложность решения недостаточно известных (в ряде случаев совсем неизвестных) отношений и определять их влияние на параметры и характеристики системы (блока) более высокого уровня в иерархической структуре членения, например летательного аппарата при его системном рассмотрении. Так как процесс проектирования — это прежде

всего процесс создания нового технического условия, которое не имеет близкого к себе прототипа, то соотношения элементов систем блоков, агрегатов, деталей летательного аппарата недостаточно известны. Поэтому в процессе проектирования при оценке альтернативных вариантов летательных аппаратов (первый уровень системного рассмотрения) и при разработке отдельных его элементов (последующие уровни рассмотрения) эти отношения должны быть тем или иным методом

спрогнозированы. Последнее означает, что степень достоверности отношений элементов проектируемого изделия будет носить вероятностный характер. Именно такой взгляд на процесс проектирования позволяет для оценки простоты или сложности вариантов разрабатываемого аппарата применять величину энтропии системы.

Рассмотрим отмеченные виды сложности (простоты) на простых отношениях, когда структура R системы представля­ет собой совокупность бинарных отношений r₁, ..., r_п.. В целях выработки методологического подхода к оценке простоты-сложности проектируемой системы представим эти отноше­ния одним видом свойств. Проанализируем взаимоотношения между элементами системы по степени изученности, напри­мер, по следующим признакам: взаимосвязь элементов может быть установлена без проведения специальных работ, для ус­тановления взаимосвязи элементов необходимо провести экс­периментальные работы. Отмеченные свойства отношений элементов системы при оценке альтернативных вариантов ее построения не могут быть точно указаны, однако их можно определить в вероятностном виде, используя метод эксперт­ных оценок.

Структурная сложность системы может быть определена в виде

(13.2.)

здесь p_i –вероятность наличия в системе i-го свойства отно­шений элементов, ее составляющих.

В отличие от формулы К. Э. Шеннона (8.1), где в теории ин­формации основанием логарифма является число 2, в выраже­нии (8.2) вычисляется натуральный логарифм вероятности p_i.Такое представление меры сложности системы аналогично за­писи Н -теоремы Больцмана.

Проиллюстрируем вариант расчета сложности на примере двух возможных альтернатив на первом уровне декомпози­ции: летательный аппарат, соответствующий полной его схе­ме, и неуправляемый реактивный снаряд. Допустим, что экс­пертный опрос показал следующие значения вероятностей i-го отношения: летательный аппарат, выполненный по пол­ной схеме: p₁ = 0,6; р₂ = 0,1; р₃ = 0,3; для снаряда: p₁ = 0,5; р₂ =0,1; р₃ =0,4.

Тогда в соответствии с (8.2) получим следующие значения величины энтропии: для первого аппарата — 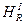= (0,6 ln 0,6 + + 0,1 ln 0,1 + 0,3 ln 0,3) = 0,896; для второго аппарата 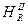= (0,5 ln 0,5 + 0,1 ln 0,1 + 0,4 ln 0,4) = 0,939.

Полученный результат говорит о том, что самолет – относительно простая система, а реактивный снаряд - более сложная.

Приведенный пример показывает, что первый аппарат, имеющий по сравнению со вторым систему наведения и уп­равления, должен быть сложнее в разработке, однако необхо­димость проведения дополнительных экспериментальных ра­бот при разработке второго аппарата (по экспертным оценкам) делает его более сложным. Необходимо сразу отметить, что предлагаемый метод оценки сложности разработки техниче­ских устройств не дает её абсолютное значение, а является лишь относительной мерой оценки альтернативных вариан­тов, он производит их ранжировку по критерию «сложность-простата».

Рассмотрим структурно-субстратную простоту (сложность) системы. Обозначив вероятность того, что отношение r₁ реализуется на произвольной паре g_f элементов m,через

меру неопределенности этого события запишем следующим образом

(13.3)

Значение энтропии для всех пар, на которых реализуется отношение r_i , будет равно

(13.4)

Энтропия, которая определяет структурно-субстратную сложность системы, тогда запишется как:

(13.5.)

здесь l – количество возможных пар элементов множества m,p_i- вероятность появления i-го свойства отношений в паре элементов множества т.

Данная мера сложности системы означает, что сложность будет зависеть не только от отношения r, но и от характера субстрата m.

Субстратно-структурная сложность (простота) системы яв­ляется противоположностью ее структурно-субстратной слож­ности. Возьмем произвольный элемент m_i множества т, со­ставляющего систему. Этот элемент в определенной степени вероятности с другими элементами множества т в отношения r₁…r_R.. Обозначим через

Вероятность наличия i-ro отно­шения относительно элемента m_j.Тогда

энтропия, приходя­щая на одно отношение r_i и один элемент m_j, может быть вы­числена по формуле:

(13.6)

а полная энтропия, приходящая на элемент m_j, получается суммированием по i-отношениям:

(13.7.)

Соответственно общая энтропия системы, соотносящая суб­страт структуре (субстратно-структурная сложность), будет равна:

(13.8.)

здесь n — число элементов т.

Рассмотренные меры различных видов сложности (просто­ты) не всегда могут соответствовать друг другу, поэтому в каждом конкретном случае необходимо критически подхо­дить к выбору оценки сложности (простоты) системы. Так, для оценки простоты летательного аппарата на этапе проекти­рования (первый уровень системного рассмотрения объекта) целесообразно рассматривать структурную простоту (слож­ность) как наиболее доступный и относительно неглубокий анализ проникновения в конструктивное построение сложно­го технического устройства. На последующих этапах разра­ботки, когда производится дальнейшая детализация изделия, где возможен широкий спектр элементов построения объекта, наиболее существенными мерами простоты (сложности) должны быть бинарные: структурно-субстратная и субстратно-структурная.

При системном подходе к процессу проектирования лета­тельных аппаратов по мере их большей детализации энтропия возрастает и в окончательном виде (отработанная конструк­ция аппарата с комплектом доработанной технической доку­ментации) достигает максимума.

С точки зрения феноменологической термодинамики для процесса проектирования справедливо также утверждение, что процесс, обратный необратимому, невозможен по опреде­лению: нельзя разработать сложное техническое устройство (выпустить рабочую документацию и изготовить опытный об­разец), отвечающее поставленным требованиям, без промежу­точных этапов его создания. Однако с точки зрения статисти­ческой физики процесс, обратный в термодинамическом смысле, есть переход от наиболее вероятного состояния к ме­нее вероятному, но возможны флуктуации, однако их вероят­ность мала. По Больцману, в системе с небольшим числом час­тиц вероятность флуктуации становится значительной, и они происходят довольно часто: достаточно простые технические устройства могут быть разработаны с минимальным количест­вом этапов, вплоть до одного (проектирование по прототипу).