ПОСТРОЕНИЕ ЛИНЕЙНЫЗ ОПТИМИЗАЦИОННЫХ МОДЕЛЕЙ
При решении производственных и коммерческих задач широко используются методы линейного программирования.
Чтобы разобраться в особенностях данного анализа, рассмотрим некоторые конкретные операции, выполняемые крыпным промышленным предприятием (например нефтеперерабатывающие заводы) с типовым технологическим процессом. Рассмотрим крупную нефтяную компанию.
Важные управляющие решения связаны со следующими процессами:
1. Геологическая разведка с целью обнаружения нефтяных месторождений;
2. Добыча сырой нефти;
3. Объем сырой нефти, добываемой фирмой на нефтесырье других нефтяных компаний;
4. Дополнительная закупка сырой нефти;
5. Доставка нефти на нефтехимические заводы;
6. Крекинг и ректификация с целью получения различных нефтепродуктов для смешения (промежуточных продуктов);
7. Получение многочисленных видов готовой продукции в результате соединения промежуточных нефтепродуктов (в различных комбинациях и процентах);
8. Доставка, транспортировка готовой продукции к местам сбыта;
9. Допустим, принимается решение смонтировать на нефтепергонном заводе дополнительную крекинг-установку. Это, естественно, отразится на производственных показателях данного предприятия. Может оказаться и то, что решение может определенным образом затронуть и все другие операции, перечисленные выше.
Проектные показатели крекинг установки могут отразиться на требованиях, предъявляемых к нефтесырью, повлиять на размещение сырой нефти, а также привести к пересмотру ассортимента выпускаемых нефтепродукции и к изменению в сфере сбыта.
Аналогичным образом увеличение (в том или ином районе) спроса на бензин сопряжено с мощностных показателей нефтеперегонных заводов. С необходимостью заключения контрактов по обмену нефтесырьем с другими нефтяными компаниями и с определением техрайонов, где следует сосредоточить основные усилия по обнаружению нефтяных месторождений.
Несмотря на очевидные упрощения приведенные ситуации являются хорошей иллюстрацией проблем . с которыми приходится сталкиваться фирмам при принятии решений, связанных с распределением ресурсов. Реальные ситуации много сложнее. Поэтому научно-обоснованный экономический анализ последствий принятия того или иного решения связан с еще большими трудностями. Однако именно такие задачи решаются с помощью методом моделй линейного программирования. Почему даже больщие и успешные компании прибегают к помощи математики? Разве управленческого опыта, интуиции и знания дела не достаточно для принятия правильных решений? Руководящие работники фирмы, отвечающие за прибыльность предприятий, давно убедились в том, что успех дела в значительной сиепени определяется качеством комплексного планирования выполняемых фирмой операций. В тоже время на больших предприятиях одна только регистрация фактических данных, необходимых для анализа сложных проблем организационного управления сопряжена с огромными трудозатратами. Людские же ресурсы фирмы, которые можно было бы использовать для оценки экономической эффективности того или иного плана ограничены.
Линейное программирование позволяет резко увеличить аналитические возможности аппарата управления фирмы. Рассматриваемые математические модели дают руководителю возможность проанализировать такой широкий спектр возможных сценариев распределения ресурсов, которого до использования этого аппарата не могло и быть. Эти результаты позволяют выявить четко определенные и исчерпывающие данные, необходимые руководителю для эффективного применения своих знаний. Машина позволяет увеличивать возможности нашего мозга . как очки зрение, к примеру.
Цель моей лекции покзать Вам ряд задач оптимизации. Решение которых предполагает построение линейных моделей. Мы не будем качаться методов решения данных задач. Это задача более углубленного курса. О Канторовиче Л.В. сказать, как о родоначальнеке линейного программирования.
Все задачи линейного программирования подразделяются на задачи:
1. Задачи распределения ресурсов
2. Транспортная задача
3. Задача составления различных сортов смесей (к примеру различных сортов нефти для получения заданного сорта бензина)
4. Комбинация рассмотренных выше задач.
ЗАДАЧА РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
| На единицу продукции А | На единицу продукции В | Имеется наличие | |||
| Технологичес- кий Процесс 1 | Технологичес- кий Процесс 2 | Технологичес- кий Процесс 3 | Технологичес- кий Процесс 4 | ||
| Количество человеко недель | 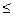 15 15
| ||||
| Количество материалов Y (кВт.час) | 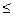 120 120
| ||||
| Количество материалов Z в кг | 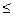 100 100
| ||||
| Доход с единицы продукции (руб) | Максимизировать | ||||
| Объем выпускаемой продукции, т | Х1 | Х2 | Х3 | Х4 |
Представим себе фирму, способную реализовать до четырех производственных процессов: 1,2,3,4. И обладающей правом выбора этих вариантов.
Технологические процессы первого и второго типов ориентированы на получение продукции А. Технологические процессы 3 и 4 ориентированы на получение продукции В.
Расходы, связанные с каждым из технологическиъ процессов, определяются трудозатратами в человеко-неделях, количеством киловатт часов, потребляемого в течение недели материала Y в количественном в кг потребляемого в течение недели материала Z.
Поскольку затраты, связанные с различными технологическими процессами не одинаковы, прибыльность процессов оказывается разной даже в том случае, когда они используются для получения продукции одного и того же вида. При составлении производственного плана на неделю диапазон возможностей предпринимателя ограничен как за счет людских ресурсов. Так и за счет потребляемого сырья, т.е. материалов Y и Z.
В рассматриваемом примере имеется три линейных неравенства ограничения на трудозатраты и материалы Y и Z. Прибыль является линейным соотношением. Максимизировать прибыль в виде:
Max(4x1+5x2+9x3+11x4) при ограничениях
x1+x2+x3+x4 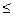 15 ограничения на человеческие ресурсы
15 ограничения на человеческие ресурсы
7x1+5x2+3x3+2x4 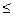 120 ограничения на материал Y
120 ограничения на материал Y
3x1+5x2+10x3+15x3 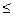 100 ограничения на материал Z.
100 ограничения на материал Z.
Дата добавления: 2015-05-28; просмотров: 1592;
