Представлення чисел в позиційній системі числення з основою р

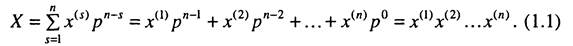До позиційних систем числення відносять системи, у яких кожна цифра займає певне положения (розряд або позицію) у ряду цифр, що зобра-жують число. Щоб одержати значения числа, потрібно кожну цифру розряду помножити на число, яке називається вагою розряду. Ваги окремих розрядів являють собою геометричну прогресію зі знаменником, що дорівнює основі системи числення р. Наприклад, розряди десяткового числа 1327,45 мають ваги: 10³= 1000; 10²= 100; 10¹= 10; 10°= 1; 10^-1=0,1; 10^-2 = 0,01. Позиційні системи числення, в яких цифри всіх розрядів набувають значения 0,1,..., р-1, а основа р є однаковою для всіх розрядів, на-зивають однорідними. Подання числа X в однорідній позиційній системі числення з основою р має вигляд:

Десяткова система або система з основою 10 (р = 10) оперує з 10 цифрами (від 0 до 9). У системах числення з основою більше 10 використовують 10 цифр для молодших значень

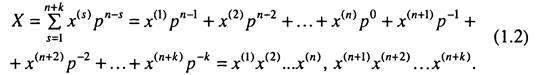
Число X, що містить п розрядів цілої частини і к розрядів дробу, можна виразити формулою

цифр розрядів і латинські літери Д, В, С... - для старших.

Якщо необхідно позначити основу системи числення, то використовують числові індекси або латинські літери: для двійкового числа ін-декс 2 або літера В (Binary), для десяткового - індекс 10 або літера D (Decimal), для шістнадцяткового - індекс 16 або літера Н (Hexadecimal).

Приклад 1.1.Записати число 11₁₀ У двійковій системі числення. У двійковій системі числення основа р = 2, а цифри розрядів можуть набувати значень 0 або 1. Згідно з формулою (1.1) число 11 ₁₀ у двійковій системі числення записують як

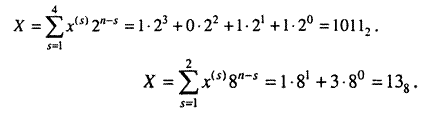Приклад 1.2.Записати число 11₁₀ у вісімковій системі числення.
У вісімковій системі числення основа р = 8, а розрядні компонента можуть набувати значень {0, 1, 2, 3,4, 5, 6, 7}. Згідно з формулою (1.1) число 11₁₀ у вісімковій системі числення можна записати так:

Приклад 1.3.Записати число 11₁₀ у шістнадцятковій системі числення. Для шістнаддяткової системи р = 16, х⁽ⁱ⁾ = {0, 1, 2, 3,4, 5, 6,7, 8, 9, A, B_t C,D_tE,F}. Згідно з формулою (1.1)

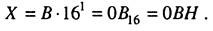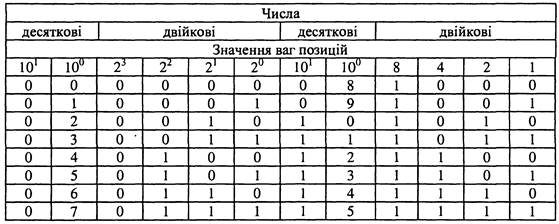
Приклад 1.4.Подати число 1327,45₁₀ у вигляді полінома (1.2). Значения ваг та цифр розрядів числа 1327,45 у десятковій системі числення ілюструє табл. 1.1 згідно з формулою (1.2):

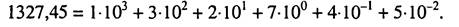Таблиця 1.1. Значения ваг та цифр розрядіву десятковій системі

Розглянуті у прикладах системи, у яких кожнш цифрі розряду відповідає окремий символ, називаються системою з безпосереднім поданням чисел.

Систему, в якій кількість символів менша, ніж кількість цифр, а кожну цифру кодують певною комбінацією кількох символів, називають системою з кодованим поданням чисел. Такою є, наприклад, двійково-десяткова система числення, яка містить десять цифр, але тільки два сим-воли, причому кожна з десяти цифр кодується числами двійкової системи: 0 =0000, 1=0001,...,9= 1001.

Приклад 1.5.Записати число 11₁₀у двійково-десятковій системі числення.

Для кожної цифри десяткового числа запишемо її двійковий еквівалент, який займає 4 розряди (1₁₀ = 000І₂). Отже, число 11₁₀ у двійково-десятковій системі буде подано таким чином:

3Системи числення з основою р=2, 8, 16

Двійкова система числення, або система з основою 2, використовує цифри 0 і l. Такі цифри називаються бітами {Binary Digits). Фізично вцифровых електронних системах значения 0 відповідає напрузі низького рівня (L-рівня), а значения 1 - напрузі високого рівня (H-рівня).

У табл. 1.2 наведено значения ваг перших чотирьох двійкових позицій і показано відповідність між двійковим числом 1001₂ та його десятковим еквівалентом 9₁₀. Розряд, якому відповідає значения ваги позиції 1, називається молодшим бітом, а розряд, якому відповідає найбільше значения ваги позиції (у цьому разі 8), - старшим бітом.

Таблиця 1.2.Значения позицій двійкових чисел

У табл. 1.3 подано десяткові числа від 0 до 15 та їх двійкові еквіваленти.

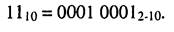Таблиця 1.3.Двійкові еквіваленти десяткових чисел від 0до 15

Вісімкова система числения.Вісімкова система - це система з основою 8, яка містить вісім цифр від 0 до 7. У табл. 1.13 подано десяткові, вісімкові та двійкові еквіваленти 16 перших чисел десяткової системи.

Таблиця 1.13. Десяткові, вісімкові і двійкові еквіваленти чисел 0-15₁₀

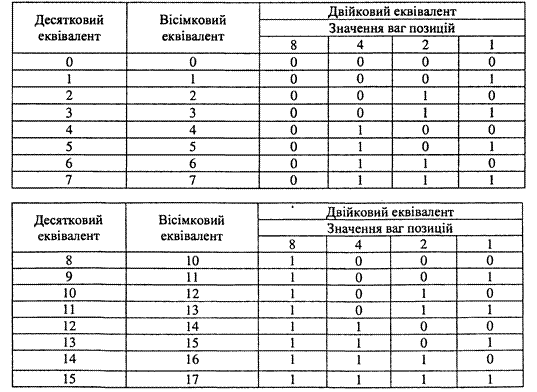Для того щоб перетворити двійкове число на вісімковий еквівалент, його ділять на тріади - групи по три біти, починаючи з молодшого біта. Якщо кількість бітів не кратна 3, то двійкове число доповнюеться нулями зліва. Потім кожну тріаду замінюють на еквівалентну вісімкову цифру відповідно до табл. 1.13. Наприклад, вісімковий еквівалент числа 11111000100₂ - це число 3704₈:

Приклад 1.13.Перетворити вісімкове число 652 l₈ на двійковий еквівалент.

Для перетворення вісімкового числа кожну його цифру замінюють двійковою тріадою:

Отже, 6521₈ = 110101010001₂.

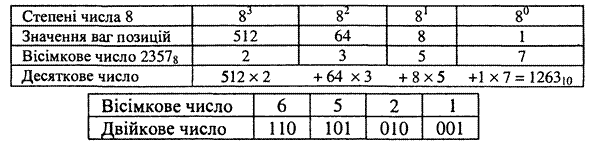
Приклад 1.14.Перетворити вісімкове число 2357₈ на десятковий еквівалент. Перетворення виконують за табл. 1.14, у другому рядку якої вказано ваги чоти-рьох перших позицій вісімкового числа. Отже, 2357₈ = 1263₁₀.

Таблиця 1.14. Вісімково-десяткове перетворення

Приклад 1.15.Перетворити десяткове число 3336₁₀ на вісімковий еквівалент.

При перетворенні десяткове число 3336₁₀ ділять на 8, що дае частку 417₁₀ і остачу 0₁₀ = 0₈. Таким чином, молодший розряд вісімкового числа мае значения 0. Частка 417₁₀ стае діленим і її знову ділять на 8, що дає частку 52₁₀ і остачу 1₁₀ = 1₈, яка стае значениям другого розряду вісімкового числа. Ділення 52₁₀ на 8 дае частку 6₁₀ і остачу 4₁₀ = 4₈. Останню частку 6₁₀ ділять на 8 із часткою 0 і остачею 6₁₀ = 6₈. Оскільки остання частка дорівнює 0, то цифра 6₈ стае значениям старшого розряду вісімкового числа:

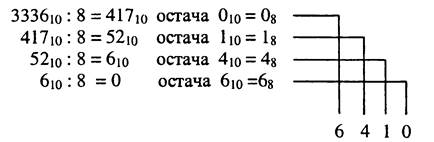
Отже, 3336₁₀ = 6410₈.

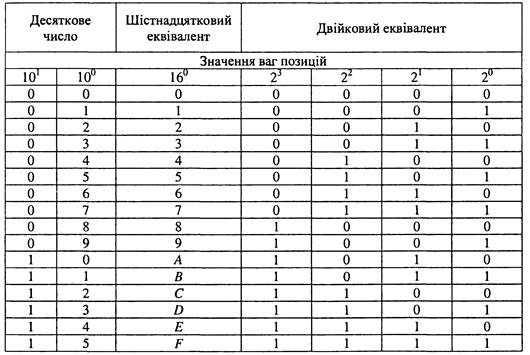
Шістнадцяткова система численияє системою з основою 16 та містить 16 символів: 0,1,2, 3,4,5,6,7, 8,9, А, В, С, D Е, F. У табл. 1.15 наведено двійкові та шістнадцяткові еквіваленти 16 перших десяткових чисел. Кож-ну шістнадцяткову цифру подають единою комбінацією чотирьох двійкових цифр. Так, шістнаддятковим еквівалентом двійкового числа 10011110₂ є число 9E₁₆. Це означає, що старшу тетраду (4 старші розряди) 1001 двійкового числа записують як 9₁₆, а молодшу тетраду 1110 - як Е₁₆.

Таблиця 1.15.Двійкові та шістнадцяткові еквіваленти десяткових чисел

Приклад 1.16.Перетворити двійкове число 11 І0І0₈ на шістнадцятковий еквівалент.

Для перетворення двійкового числа на шістнадцятковий еквівалент треба поділити його на тетради, починаючи з наймолодшого розряду, а потім кожну тетраду замінити еквівалентною шістнадцятковою цифрою. Значения молодшої тетради 1010₂ = А₁₆ старшої- 0001₂ = 3₁₆. Отже, 111010₂ = ЗА₁₆.

Приклад 1.17.Перетворити шістнадцяткове число 7F₁₆ на двійковий еквівалент. Для перетворення шістнадцяткового числа на двійковий еквівалент кожну шістнадцяткову цифру слід замінити на двійковий еквівалент - тетраду (див. табл. 1.15). Еквівалентом шістнадцяткової цифри 7₁₆ є двійкове число 0111₂, а цифри F₁₆- число 1111₂. Отже, 7F₁₆ = 01111111₂.

Приклад1.18. Перетворити шістнадцяткове число 2С6Е₁₆ на десятковий еквівалент.

Перетворення виконують згідно з табл. 1.16. Кожну цифру шістнадцяткового числа множать на відповідну вагу позиції. Сума цих добутків дає десяткове число 11374₁₀.

Таблиия 1.16.Перетворення шістнадцяткового числа на десяткове

Приклад 1.19.Перетворити десяткове число 15797 на шістнадцятковий еквівалент.

При перетворенні десяткове число 15797 ₁₀ ділять на 16, що дає частку 987₁₀ і остачу 5₁₀ = 5₁₆. Таким чином, молодший розряд шістнадцяткового числа мае значения 5. Частка 987₁₀ стае діленим і ії знову ділять на 16, що дае частку 61₁₀ і остачу 11₁₀ = B₁₆, яка стає значениям другого розряду шістнадцяткового числа. Ділення 61₁₀ на 16 дає частку З₁₀ і остачу 13₁₀ = D₁₆. Ділення З₁₀ на 16 дае частку 0 і остачу З₁₀ = З₁₆. Оскільки остання частка дорівнює 0, то цифра З₁₆ стає значениям старшого розряду шістна-дцяткового числа:

Отже, 15797₁₀ = 3DB5₁₆.

Двійково-десяткова система числения- система, у якій кожну десяткову цифру від 0 до 9 подають 4-розрядним двійковим еквівалентом. Та-ка система числения дозволяе скоротити програмні та апаратні витрати при перетворенні двійкових чисел, які використовують під час обробки інформації у процесорі, на десяткові, що виводять на пристрої відображення. Ця система є ефективною і при перетворенні десяткових чисел на двійкові. Двійково-десяткові числа записують з індексом 2-10 або ДЦК (двійково-десятковий код), наприклад 01001001_2-10, 0100ддк.

Приклад 1.20.Перетворити десяткове число 3691₁₀ на двійково-десятковий код. При перетворенні кожну цифру десяткового числа перетворюють на двійковий 4-розрядний еквівалент:

Отже, 3691₁₀ = 0011 0110 1001 0001_2-10

Приклад 1.21.Перетворити двійково-десяткове число 1000000001110010_2-10 на десятковий еквівалент.

Кожна тетрада двійково-десяткового числа перетворюється на десятковий еквівалент:

Отже, 1000 0000 0111 0010_2-10 = 8072₁₀.

Дата добавления: 2015-05-28; просмотров: 6298;