Расчетные соотношения для случая резервирования при идеальных переключающих устройствах (коммутаторах)

В общем виде основные показатели надежности технической системы, при резервировании замещением могут быть вычислены по следующим, уже известным формулам.

Математическое ожидание времени работы системы до отказа:

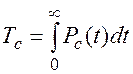(8.1)
Частота отказов системы:

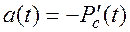(8.2)
Интенсивность отказов системы:

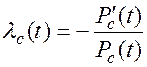(8.3)
Здесь Р_С(t) –– функция надежности технической системы.

Вероятность безотказной работы системы при «холодном» резервировании будем вычислять при следующих допущениях:

все резервные устройства до момента замещения основной системы равнонадежны;

переключающие устройства в смысле надежности идеальны;

ремонт резервированной системы в процессе ее работы невозможен.

Пусть первоначально техническая система состоит из одного рабочего и одного резервного устройства. Основное устройство обозначим через А, резервное –– через В.

С учетом принятых допущений отказ системы в течение времени t будет отсутствовать в случае: а) устройство А в течение времени t не отказало; б) устройство А отказало в момент времени t, а устройство Б, будучи исправным до момента замещения t, осталось исправным и в течение времени (t-t)

Рис. 8.1. Представление процесса функционирования дублированной системы при «холодном» резервировании

На основании формулы полной вероятности вероятность P_c(t) безотказной работы резервированной системы в течение времени t может быть представлена в виде:

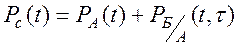(8.4)
где P_A(t) –– вероятность безотказной работы устройства А в течение времени t;

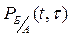–– вероятность безотказной работы устройства Б в течение времени t при условии, что отказ системы А произошел в момент t.

Определим вероятность .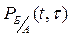

Рис. 8.2. Распределение частоты отказов системы А

Момент времени t замещения основного устройства является величиной случайной. Пусть функция распределения времени повреждения устройства А (частота отказов устройства А) имеет вид, представленный на рис. 8.2.

Разобьем ось времени на равные интервалы:

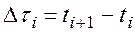(8.5)
Тогда вероятность возникновения отказа системы в течение произвольно выбранного промежутка Dt_i можно записать в виде:

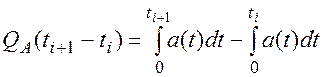(8.6)
При малом значении Dt_i эта вероятность будет пропорциональна длине интервала:

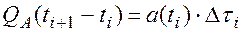(8.7)
Вероятность безотказной работы резервного устройства до момента t запишется в виде:

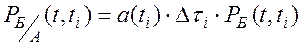(8.8)
где: 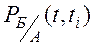–– вероятность безотказной работы резервного устройства на интервале t-t_i при условии, что до момента t_i устройство Б было исправно; первые два сомножителя определяют вероятность отказа устройства А до момента t_i согласно (8.7); 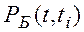–– вероятность исправной работы устройства Б технической системы на интервале (t, t_i).

Вероятность возникновения отказа в промежутках времени Dt₁, Dt₂, …, Dt_n, очевидно, будет соответствовать a(t₁) ×Dt₁, a(t₂) ×Dt₂,…, a(t_n)×Dt_{n .}

Тогда, принимая отказы устройства А в любой промежуток времени Dt в качестве гипотез, на основании формулы полной вероятности можно найти вероятность безотказной работы резервированной системы:

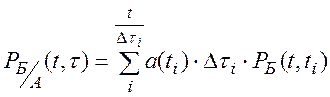(8.9)
Уменьшая промежуток Dt_i и переходя к пределу, получим:

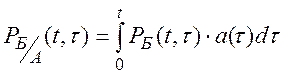(8.10)
Подставляя это выражение в формулу полной вероятности, имеем:

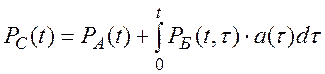(8.11)
где t –– случайный момент замещения отказавшего устройства.

Это выражение позволяет получить общую формулу вероятности безотказной работы системы с любой кратностью резервирования.

Система с кратностью резервирования m может быть представлена системой, имеющей кратность резервирования m-1 и одного резервного устройства. Тогда, повторяя приведенные выше рассуждения, получим следующее выражение для вероятности безотказной работы системы с кратностью резервирования m:

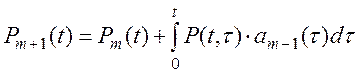(8.12)
где P_m(t) –– вероятность безотказной работы системы с m-1 резервным устройством (всего в системе m устройств) в течение времени t; P(t,t) –– вероятность безотказной работы одного резервного устройства в течение времени (t-t), при условии, что до момента t оно было исправно; a_m-1(t) –– функция распределения времени повреждения системы с кратностью резервирования (m-1), или, что то же самое, частота отказов.

Поскольку

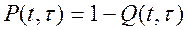(8.13)
получим:

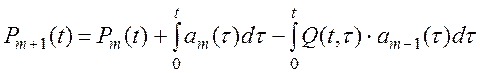(8.14)
Учитывая, что:

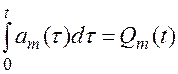(8.15)
имеем:

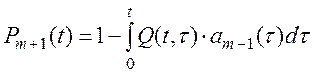(8.16)
или

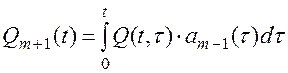(8.17)
В рамках принятых допущений, считая, что условия и режимы работы резервных устройств облегчены настолько, что практически они начинают терять надежность только с момента замещения отказавшего устройства, т.е. отказ резервной системы до момента t произойти не может, справедливы соотношения:

,

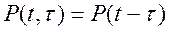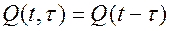
тогда рекуррентное уравнение (8.12) с учетом (8.15) принимает вид:

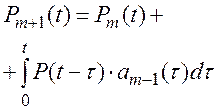(8.18)

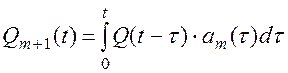
Приведенные формулы не всегда удобны для практического использования, поскольку для вычисления вероятности безотказной работы и вероятности отказа системы, резервированной m раз, необходимо вычислять частоту отказов системы, резервированной m-1 раз. Эти зависимости могут быть существенно упрощены.

Используем интегрирование по частям, для чего обозначим:

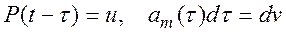
Тогда:

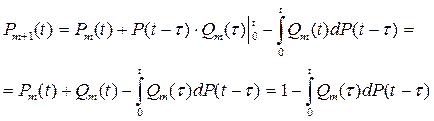(8.19)
Или

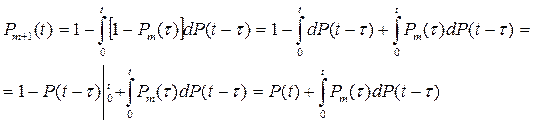
Окончательно имеем:

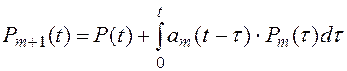
	(8.20)
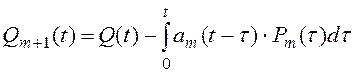
	(8.21)

где P(t), Q(t) –– вероятность безотказной работы и вероятность отказа резервного устройства с момента его включения и до момента t.

Из этих формул видно, что для вычисления 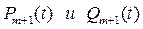нет необходимости рассчитывать частоту отказов резервированной системы. Эти формулы весьма удобны для вычисления вероятности безотказной работы и отказа, если известно аналитическое выражение .

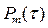Однако на практике чаще встречаются задачи, когда требуется по известной вероятности безотказной работы нерезервированной системы вычислить вероятность безотказной работы системы с m-кратным резервированием.Для решения этой задачи по формулам (8.20),(8.21) необходимо вначале вычислить вероятность безотказной работы дублированной системы (m=1), затем, используя полученный результат, вычислить вероятность безотказной работы резервированной системы при m=2 и т.д. Таким образом, задача фактически сводится к отысканию m-кратного интеграла.При экспоненциальном законе распределения отказов в системе с «холодным» резервированием частоты отказов основного устройства (индекс 0) и резервных устройств будут иметь вид:

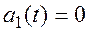при t £ t₀

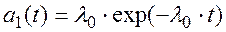при t₀ < t < t₁

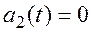при t <t₁

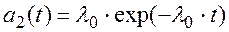при t₁ < t < t₂

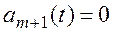при t £ t_m

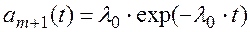при t_m < t < t_m+1

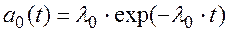при t < t₀

где l₀ –– интенсивность отказов основного или любого резервного устройства; t_i –– время отказа i-го устройства, отсчитанное от момента включения всей резервированной системы.

Вычислим вероятность безотказной работы системы, пользуясь формулой (8.20).

При m=1:

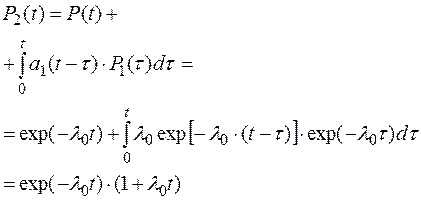
При m=2:

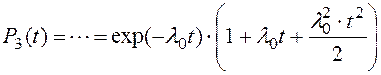
При m=3:

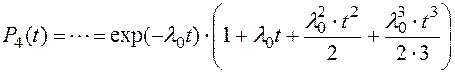
При произвольной кратности резервирования m:

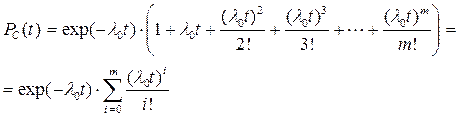
Или

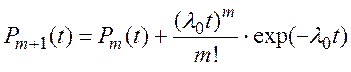(8.22)

Выражение для времени безотказной работы системы имеет вид:

,

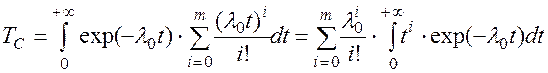где интеграл 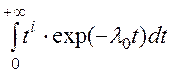–– эйлеров интеграл второго рода.

Известно, что ( см. Приложение 1):

,

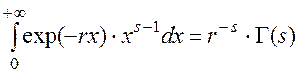тогда:

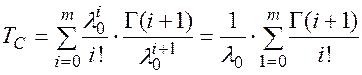
Используя свойства гамма-функции (см. Приложение 1):

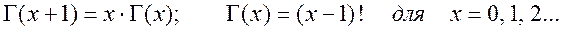
Выражение для среднего времени безотказной работы системы с m-кратным «холодным» резервированием может быть представлено в следующем простом виде:

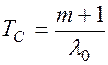(8.23)
Дисперсия времени возникновения отказов системы в этом случае может быть вычислена по формуле:

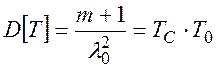(8.24)
Среднее квадратическое отклонение времени возникновения отказов:

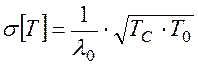(8.25)

Функция интенсивности отказов системы при m-кратном «холодном» резервировании определяется соотношением:

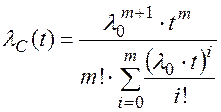(8.26)
Функция частоты отказов системы в этом случае имеет вид:

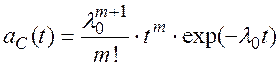
(8.27)