Теоретические предпосылки решения задачи расчета надежности технической системы, резервированной по принципу «теплого» резерва.

До сих пор мы рассматривали системы, надежность дублирующих устройств которых не зависела от момента включения этих устройств в работу. Гораздо сложнее выглядит расчет надежности реальной системы, резервное устройство которой может отказывать до включения в работу с меньшей плотностью отказов, чем при включении в активное замещение отказавшего устройства.

Существенное повышение надежности может достигаться путем применения так называемого нагрузочного или «теплого» резервирования. В процессе проектирования сложных технических систем конструктор может во многих случаях уменьшить нагрузку на отдельные (резервные) устройства или элементы системы более чем в 10 раз по сравнению с нормальной. При этом интенсивность отказов резервных устройств остается постоянной во времени и, как правило, линейно убывает с уменьшением коэффициента нагрузки.

Сравнение показателей надежности систем, резервированных различными способами, показывает, что нагрузочное резервирование может быть более эффективным в системах, предназначенных для длительной работы в относительно стабильных условиях.

Допустим, что техническая система состоит из одного основного и одного резервного устройства, работающих «параллельно». Интенсивность отказов основного устройства обозначим через l₀(t). При отказе основного устройства происходит мгновенное безотказное автоматическое переключение работы на второе (резервное) устройство. Интенсивность потока отказов резервного устройства до его включения в работу обозначим через l₁(t). После включения резервного устройства в работу интенсивность потока его отказов мгновенно подскакивает (рис.7.1) до значения 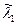, которую естественно полагать зависящей не только от текущего момента времени t, но и от того срока t₀, в течение которого элемент работал в облегченном режиме:

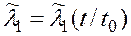(7.1)
Рассмотрим совокупность двух случайных величин:

Т₀ –– случайный момент отказа основного устройства;

Т₁ –– случайный момент отказа резервного устройства.

Пусть событие А –– безотказная работа технической системы до момента времени t –– состоит в том, что хотя бы одна из величин (Т₀, Т₁) примет значение, превышающее t (одно из устройств сохранит к этому моменту времени свою работоспособность). Т.е. вероятность 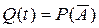того, что в момент t рассматриваемая система откажет будет соответствовать вероятности того, что случайные величины Т₀ и Т₁ примут значения меньше величины t:

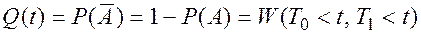(7.2)
Пусть t₀ –– фиксированный момент отказа основного устройства системы; t₁ –– фиксированный момент отказа резервного устройства.

Рис. 7.1. Общее представление характера изменения интенсивности отказов резервного устройства

Найдем совместную плотность 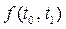распределения случайных величин Т₀ , Т₁. Поскольку эти случайные величины зависимы, то:

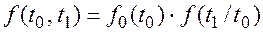(7.3)
где 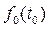–– безусловная плотность распределения случайной величины Т₀; 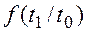–– условная плотность распределения величины Т₁ (при условии, что случайная величина Т₀ приняла значение t₀).

Как было определено ранее, плотность распределения случайного времени отказа (в общем случае) можно выразить через интенсивность отказов:

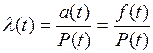
Следовательно, плотность распределения времени отказа основного устройства:

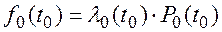(7.4)
где 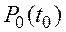–– надежность основного устройства технической системы, в общем случае равная:

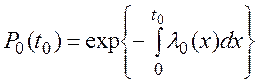(7.5)
Тогда:

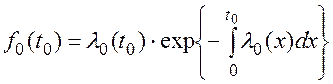(7.6)
Условная интенсивность отказов резервного устройства при условии, что случайная величина Т₀ принимает значение t₀ определяется зависимостями:

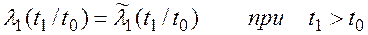
(7.7)

Вероятность безотказной работы резервного устройства при t₁< t₀ (резервное устройство отказывает раньше выхода из строя основного, не успев включиться в активный режим работы и не изменив интенсивности l₁(t) отказов) равна:

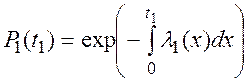
В случае отказа резервного устройства после его включения в активный режим работы (после отказа основного устройства), т.е. в случае t₁ > t₀ эта вероятность определится соотношением:

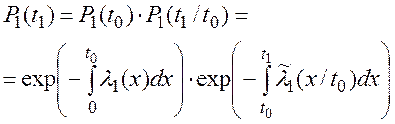
Теперь может быть определена условная плотность 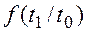распределения времени безотказной работы резервного устройства:

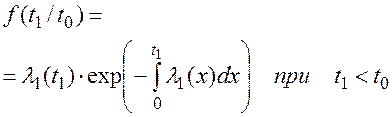(7.8)

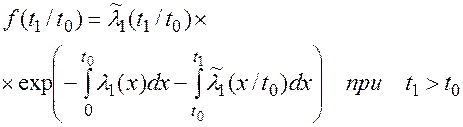(7.9)
Таким образом, совместная плотность распределения случайных величин Т₀ и Т₁ может быть определена с помощью зависимостей:

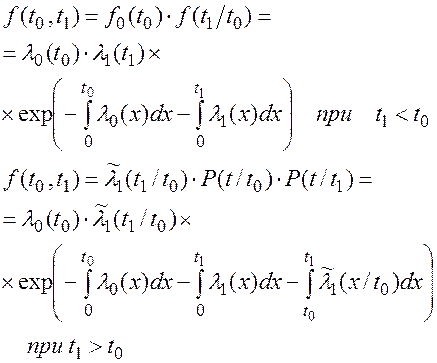(7.10)

Зная эту совместную плотность, можно найти вероятность отказа системы до интересующего момента t:

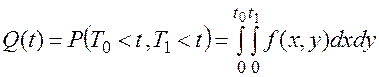(7.11)

Следовательно, надежность технической системы (вероятность ее безотказной работы в течение времени t) определится уравнением:

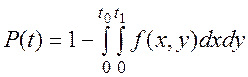(7.12)

При вычислениях по формулам (7.10), (7.11), (7.12) необходимо иметь в виду, что плотность 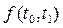имеет различные выражения по разные стороны биссектрисы первого координатного угла или прямой t₀=t₁ (рис. 7.2 ).

Рис. 7.2. Области интегрирования для вычислении надежности технической системы при нагрузочном резервировании

В области I выражение для плотности определяется первой зависимостью в формуле (7.10), т.е. при t₁<t₀. В области II –– второй зависимостью в той же формуле (при t₁>t₀). Следовательно:

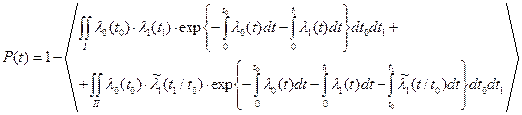(7.13)
Если вид функций l₀(t), l₁(t), 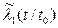известен, то интеграл (7.13) может быть вычислен, в простейших случаях аналитически, чаще – численно.

Приведенные выше рассуждения свидетельствуют о том, что даже в случае одного резервного устройства, работающего в облегченном или нагрузочном режиме, задача вычисления надежности технической системы довольно сложна. Если же число резервных устройств будет более одного, то решение усложняется весьма существенно.

Однако задача может быть значительно упрощена, если предположить, что потоки неисправностей, действующие на все устройства (основное и резервные), представляют собой простейшие потоки, интенсивность отказов каждого из которых постоянна, что равносильно тому, что закон надежности каждого устройства экспоненциальный, и включение устройства в работу меняет только параметр этого закона.

При таком допущении надежность технической системы может быть найдена путем решения системы дифференциальных уравнений для вероятностей ее состояний.