Формула полной вероятности. Если до проведения опыта вероятности реализации гипотез Н1, Н2, , Нn были Р(Н1), Р(Н2), , Р(Нn), и в результате опыта появилось событие А
Если до проведения опыта вероятности реализации гипотез Н1, Н2,…, Нn были Р(Н1), Р(Н2),…, Р(Нn), и в результате опыта появилось событие А, то с учетом этого факта «новые», т.е. условные вероятности гипотез вычисляются по формуле Бейеса, которая дает возможность «пересмотреть» априорные вероятности гипотез с учетом результата проведенного опыта:
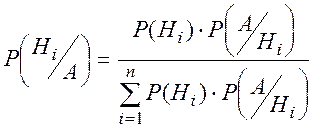 (2.11)
(2.11)
Если об обстановке опыта можно сделать n исключающих друг друга предположений (гипотез) Н1, Н2, …, Нn и если событие А может появиться только при одной из этих гипотез, то вероятность реализации события А вычисляется по формуле полной вероятности:
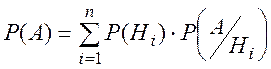 (2.12)
(2.12)
Если после опыта, закончившегося появлением события А, производится еще один опыт, в котором может появиться или не появиться событие В, то вероятность (условная) появления этого события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез {Р(Hi)}, а новые { 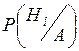 }:
}:
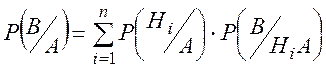 (2.13)
(2.13)
Задача 2.15.
Прибор может работать в двух режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора. Ненормальный режим –– в 20%. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0.1, в ненормальном - 0,7.
Найти безусловную вероятность Р выхода прибора из строя за время t.
Ответ.
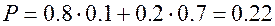
Дата добавления: 2015-05-26; просмотров: 1318;
