Метод дискретного счета.

При методе дискретного счета используют закономерности апериодического процесса, возникающего при подключении заряженного конденсатора или катушки индуктивности с протекающим в ней током к образцовому резистору. При измерении активного сопротивления применяют процесс разряда образцового конденсатора через измеряемый резистор. При этом измеряемый интервал времени функционально связан с преобразуемым параметром. Преобразователи отличают высокая точность и быстродействие.

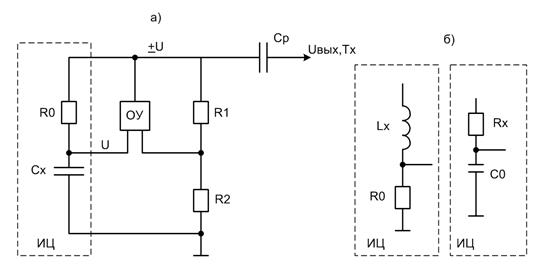
Измерительная цепь (ИЦ) интегрирующего типа с образцовым Ro и постоянной величиной времени τх=RoCx питается выходным напряжением ОУ, являющимся основным элементом сравнения – компаратором. Отметим, что классический ОУ питается двумя разнополярными напряжениями, которые поочередно служат выходными напряжениями, выделяемыми разделительным конденсатором Ср. Порог срабатывания компаратора задают сопротивлениями R1 и R2. При поступлении в момент времени to на измерительную цепь с выхода ОУ постоянного напряжения Uo происходит его интегрирование измерительной цепью. При этом напряжение на инвертируемом входе ОУ равно:

u(t)=Uo(1+β)(1-e^-t/τx)-βUo (1)

где β=R2/(R1+R2) – коэффициент передачи цепи ПОС.

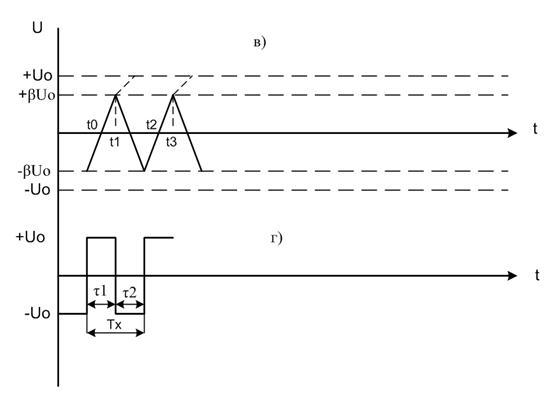
При достижении напряжения u(t)= u порогового значения +βUo (момент времени t1 на эпюре в) компаратор срабатывает и изменяет на выходе знак Uo на противоположный. При этом интервал интегрирования равен:

T1=t1-t0=τx*ln(1+β)/(1-β) (2)

На следующем интервале времени τ=t2-t1 происходит формирование развертывающей функции с противоположным знаком производной. Очевидно, при равенстве значений положительного и отрицательного порогов срабатывания абсолютные величины +βUo и –βUo равны, интервалы τ1 и τ2 равны. Период напряжения на выходе ОУ:

Тх=Т1+Т2=2τх*ln(1+β)/(1-β) (3)

Этот интервал измеряют цифровым измерителем или частотомером. Результат измерения периода Тх пропорционален значению определяемого параметра. В данном случае Rx.