Теория активных столкновений.

Теория активных столкновений использует основные положения молекулярно - кинетической теории и предположение о существовании энергетического барьера. Для объяснения механизма химического взаимодействия в соответствии с этой теорией полагают, что молекулы реагентов - маленькие твердые шарики, находящиеся в беспрерывном хаотическом движении, средняя энергия которого определяется температурой системы. Столкновения молекул, обладающих энергией активации, являются эффективными и ведут к химическому превращению. Теория позволяет рассчитать число эффективных столкновений, а следовательно, и скорость химической реакции.

Для гомогенной реакции вида:

Н_2(Г) + I_2(Г) = 2НI_(Г) ,

число двойных столкновений (Z) в 1 с в 1 м³ составит:

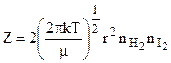, (10.27)

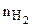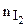где и - числа молекул Н₂ и I₂ в 1 м³;

k - постоянная Больцмана, равная 1,38 10^-23 Дж/К;

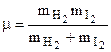- приведенная масса сталкивающихся молекул;

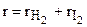- сумма радиусов молекул.

Если считать, что все двойные столкновения приводят к образованию конечного продукта, то есть Z = v, то при 700 К и р = 1,01 10⁵ Па, Z = 10²⁸. Это значило бы, что реакция состоялась бы за 10^-10 с. Однако наблюдаемая скорость на много порядков меньше, то есть не каждое столкновение молекул приводит к осуществлению химической реакции.

Можно допустить, что акт химического взаимодействия осуществляется лишь тогда, когда молекулы выгодно ориентированы в пространстве в момент столкновения. Это предположение может быть учтено введением стерического фактора или геометрической вероятности ( ).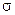

Тогда v = 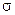Z. Однако такой подход не согласуется с опытными данными.

Во-первых, не может быть объяснена резкая температурная зависимость скорости реакции, вследствии того, что величина Z слабо изменяется с изменением температуры .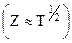

Во-вторых, для согласования с экспериментальными данными величина должна была бы составить значение 10^-14 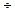10^-15, что трудно объяснимо.

Следовательно, условием протекания акта химического превращения является не особое геометрическое расположение в пространстве сталкивающихся молекул, а их повышенный запас энергии. Другими словами реакция состоится, если энергия относительного давления молекул по линии их столкновения превысит некоторую критическую величину, то есть энергию активации.

Если 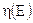- доля молекул, обладающих энергией, не меньшей энергии активации Е, то скорость реакции вычислится из уравнения:

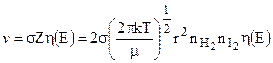, (10.28)

где 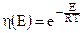(из закона распределения Максвелла - Больцмана).

Рассматриваемая реакция бимолекулярная, потому в соответствии с законом Гульдберга - Вааге

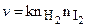. (10.29)

Сравнение (10.28) и (10.29) дает:

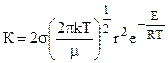. (10.30)

После интегрирования:

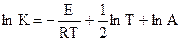, (10.31)

где А - постоянная, включающая величины r, 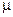и .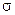

Сопоставляя (10.31) с уравнением Аррениуса (10.25) можно видеть, что теория активных столкновений в общем удовлетворительно объясняет наблюдаемую на опыте зависимость константы скорости реакции от температуры, так как величина 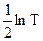слабо зависит от температуры.