Молекулярность и порядок химической реакции.

Химические реакции разделяются по признаку их молекулярности или по признаку порядка химической реакции.

Молекулярность химической реакции равна числу молекул (или других частиц), одновременным воздействием между которыми осуществляется элементарный акт химического превращения.

В зависимости от числа таких частиц различают моно (одно-) молекулярные, би (двух-) молекулярные и три (трех-) молекулярные реакции.

Мономолекулярные реакции - реакции разложения молекул:

I₂ = 2I.

Для нее закон Гульдберга - Вааге дает:

.

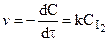К бимолекулярным реакциям относятся взаимодействия двух одинаковых или различных молекул:

Н₂ + I₂ = 2НI,

.

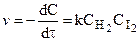К тримолекулярным относятся реакции вида:

2NO + Н₂ = N₂O+Н₂O (a)

или

Н₂ + 2О₂ = 2Н₂O, (b)

для которых справедливы соотношения:

,

.

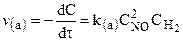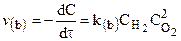Молекулярность реакции - понятие теоретическое. Для того, чтобы знать молекулярность, нужно представлять, как именно протекает данная реакция, через взаимодействия каких молекул, через какие стадии.

В противоположность молекулярности порядок реакции - экспериментальная величина. Он связан с опытной зависимостью скорости данной реакции от концентрации исходных продуктов.

Порядок реакции равен сумме показателей степеней концентраций в уравнении, выражающем зависимость скорости реакции от концентрации и устанавливаемом экспериментально.

Для простых реакций, протекающих в полном соответствии с их стехиометрическим уравнением, порядок и молекулярность численно совпадают.

Причины несовпадения порядка реакции и ее молекулярности таковы.

А. Один из реагентов находится в большом избытке. Тогда в ходе реакции его концентрация изменяется незначительно и в уравнении закона Гульдберга - Вааге может быть принята постоянной.

В. Если данная реакция гетерогенная, то в зависимости от условий ее протекания порядок химической реакции изменяется.

С. Порядок каталитических реакций также может отличаться от молекулярности. Причина - сложный механизм таких реакций, не отражаемый стехиометрическим уравнением.

D. Наконец, для сложной реакции, протекающей в несколько стадий, характерно то, что основное влияние на скорость реакции может оказать какая-либо промежуточная стадия, которая и определит, в конечном итоге, порядок всей реакции.

Например, порядок реакции разложения пентаоксида азота

2N₂O₅ = 2N₂O₄ + O₂,

казалось бы, должен быть равен двум.

Исследования показали, что реакция протекает в несколько стадий (результаты анализа химического состава газовой фазы):

N₂O₅ = N₂O₃ + O₂, (1)

N₂O₃ = NO₂ + NO, (2)

NO + N₂O₅ = 3NO₂, (3)

4NO₂ = 2 N₂O₄, (4)

причем стадия (1) является наиболее медленной, а поэтому и определяющей скорость всего процесса. Поэтому и суммарная реакция - бимолекулярная реакция первого порядка.

По признаку “порядок химической реакции” различают реакции нулевого, первого, второго и третьего порядков.

Если реакция протекает по нулевому порядку, то

,

отсюда

-dC = kd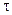

и после интегрирования в интервале от С₀ до С за время от 0 до :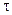

С - С₀ = -k 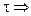С = С₀ - k 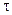. (10.6)

Следовательно, в реакциях нулевого порядка концентрация линейно уменьшается со временем. Уравнение (10.6) - кинетическое уравнение реакции нулевого порядка.

Период полураспада (полупревращения) 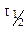, равный времени, за которое концентрация исходного продукта уменьшается в два раза (С = 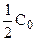) составит:

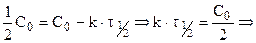
окончательно

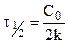. (10.7)

Константа скорости может быть найдена из (10.6):

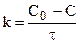. (10.8)

Выражение для скорости реакции первого порядка:

.

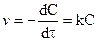После разделения переменных и интегрирования от 0 до 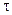при изменении концентрации от С₀ до С:

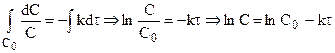, (10.9)

и окончательно:

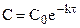, (10.10)

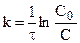. (10.11)

Подставляя 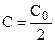, уравнение для расчета периода полураспада:

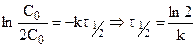. (10.12)

Таким образом, для реакции первого порядка выполняются следующие закономерности: зависимость концентрации от времени экспоненциальная; зависимость логарифма концентрации от времени линейная; период полураспада не зависит от начальной концентрации.

При равенстве концентраций исходных продуктов реакции кинетические уравнения реакций второго и третьего порядков соответственно запишутся:

и .

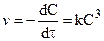После разделения переменных:

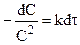и ,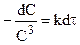

и после интегрирования:

и 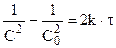. (10.13)

Из (10.13) для реакции второго порядка:

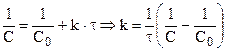. (10.14)

Полагая, что 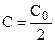для :

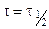. (10.15)

Для реакции третьего порядка:

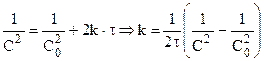, (10.16)

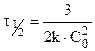. (10.17)

Таким образом для реакций второго порядка наблюдается линейная зависимость 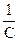от времени (10.14), а период полураспада обратно пропорционален начальной концентрации. Для реакций третьего порядка наблюдается линейная зависимость от времени величины, обратной квадрату концентрации исходного продукта реакции. Период полураспада таких реакций обратно пропорционален квадрату начальной концентрации.

При интегрировании кинетических уравнений удобно обозначать концентрации реагентов с помощью изменения концентрации x одного из них в момент времени 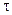. Тогда x = C₀ - C и уравнения (10.10 и (10.11) примут вид:

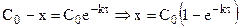(10.18)

и

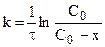. (10.19)

Эти уравнения можно получить, составив кинетическое уравнение вида:

и проинтегрировав его в интервале от 0 до 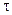при изменении x от 0 до x.

Для реакции второго порядка кинетическое уравнение выглядит:

,

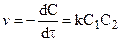если .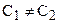

Тогда с учетом :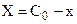

.

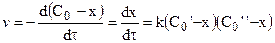Отсюда:

,

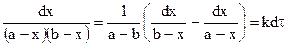где а = С₀’, a b = C₀’’.

Далее после интегрирования:

и, наконец

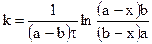. (10.20)

Для реакции третьего порядка, ограничиваясь случаем. когда две начальные концентрации одинаковы и равны а (С₀’ = C₀’’ = a), а третья начальная равна b (С₀’’’ = b), уравнение для расчета константы скорости примет вид:

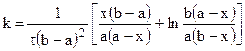. (10.21)