Термодинамика неидеальных растворов.

Полученные ранее соотношения непосредственно для описания равновесий с участием реальных растворов не могут быть использованы. Построение общей теории реальных растворов невозможно ввиду их многообразия.

Простое и универсальное решение этой задачи выполнил американский физико-химик Гилберт Ньютон Льюис. Он предложил учесть отклонения в поведении реальных растворов от идеальных заменой концентрации раствора его активностью (а_i). После такой замены форма записи законов сохраняется прежней и удовлетворяет опытным данным.

Основная характеристика, описывающая поведение любого компонента раствора - его химический потенциал . Для случая реального раствора:

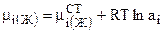, (7.47)

где - химический потенциал компонента в стандартном состоянии.

Очевидно, что стандартное состояние характеризуется значением a_i = 1.

Стандартное состояние выбирается в зависимости от концентрации исследуемого реального раствора и удобства измерения давления насыщенного пара в этом состоянии. Существуют следующие варианты стандартных состояний:

а) состояние чистого компонента, достигаемое экстраполяцией закона Рауля до N_i = 1;

б) гипотетическое состояние, достигаемое экстраполяцией закона Генри до N_i = 1;

в) состояние компонента в растворе с его массовым процентом, равном единице.

Расчет a_i можно выполнить по нижеследующей схеме.

Если реальный раствор находится в равновесном состоянии, то:

,

где 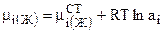, а 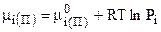, тогда

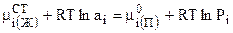. (7.48)

Для стандартного состояния, как и для любого другого, справедливо равенство:

,

где

. (7.49)

Равенство (7.48) с учетом (7.49) принимает вид:

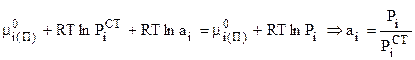. (7.50)

Для случая концентрированных растворов (вариант а) активность растворенного вещества ( ) определяет отклонения от закона Рауля:

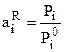, (7.51)

где Р_i - давление насыщенного пара над реальным раствором;

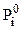- давление насыщенного пара над чистым компонентом.

Из закона Рауля следует:

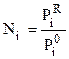. (7.52)

Совместное решение (7.51) и (7.52) дает:

,

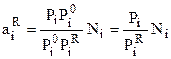где 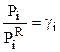- коэффициент активности.

Окончательно:

. (7.53)

Для случая разбавленных растворов (вариант б) активность растворенного вещества ( 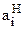) устраняет отклонения от закона Генри:

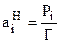, (7.54)

где Г - постоянная Генри или давление насыщенного пара i-го компонента над раствором в

стандартном состоянии.

Из закона Генри следует, что:

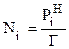. (7.55)

Совместное решение (7.52) и (7.53) позволяет получить соотношение:

,

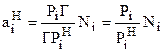где 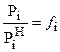- коэффициент активности.

Тогда окончательно:

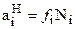. (7.56)

Если в растворе имеет место реакция А + 2В = 3С, то закон действующих масс запишется:

, (7.57)

где 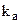- константа равновесия;

а_А, а_В, а_С - активности продуктов химической реакции.

Уравнение изотермы химической реакции с участием растворов приобретает следующую форму записи:

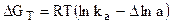, (7.58)

где 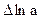- алгебраическая сумма логарифмов начальных активностей реагентов.