Неравновесная термодинамика

Выше изложенные положения классической (равновесной) ТД верны для изолированных и закрытых систем и описывают системы, находящиеся в состоянии термодинамического равновесия.

Неравновесная термодинамика подразделяется на линейную и нелинейную.

Линейная рассматривает процессы, протекающие вблизи равновесия.

Нелинейная – вдали от него.

Уравнение Пригожина и его анализ:

Уравнение Пригожина позволяет решить вопрос применимости второго закона термодинамики к открытым системам.

Согласно II-му закону ТД:

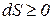
Пригожин предложил разбить общее изменение энтропии на два слагаемых:

,

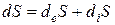где 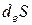- изменение энтропии за счет обмена энергией и веществом с внешней средой,

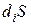-изменение энтропии за счет протекающих в системе необратимых процессов, и оно всегда больше нуля: 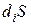> 0.

В стационарном состоянии, если 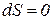, то .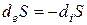

Если изменение энтропии за счет необратимых процессов всегда больше нуля, то свободная энергия Гиббса связана с выражением:

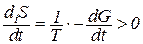
В результате возможно осуществление нескольких вариантов:

1) Если 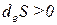, то и ;

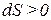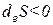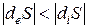2) Если , а , то ,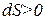

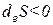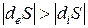3) Если , а , то .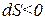

Последний вариант является лишь кажущимся отклонением от II-го закона термодинамики, так как процесс обмена: 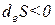идет заведомо против градиента и осуществляется за счет внешних сил, т.е. работа совершается над системой. Это просто следствие некорректной формулировки – открытую систему в этом случае с точки зрения термодинамики нельзя изолировать от среды, необходимо раздвинуть границы и тогда с соблюдением параметров новой открытой системы - общее изменение энтропии сменит знак: .

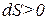Неравновесная линейная термодинамика необратимых процессов

Основы неравновесной линейной термодинамики заложены Онзагером и развиты Пригожиным. Согласно ее положениям допускается, что, даже если система в целом не равновесна, каждая из подсистем может находиться в состоянии равновесия (принцип локального равновесия).

Таким образом, неравновесная линейная термодинамика рассматривает процессы вблизи термодинамического равновесия, когда между потоками и силами существует линейная зависимость.

Изменение энтропии в открытых системах

Для анализа изменений энтропии в открытых системах вводится понятие локальная скорость энтропии s в элементарном объёме .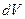

На основании этого допущения, в неравновесной термодинамике можно использовать основные положения равновесной и тогда изменение энтропии можно считать равным:

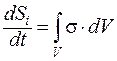, а так как 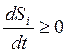, - то и s³0.

Эта функция универсальна для всех термодинамических процессов. Например, для химической реакции она равна: 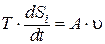, где

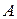- сродство химической реакции,

а u – скорость реакции.

Таким образом, эта функция, отражающая в общем случае произведение силы – 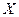на поток – 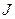, получила название диссипативная функция:

,

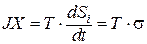Если в открытой системе протекает 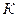- процессов, она равна:

.

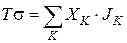Таким образом, и в открытой системе протекание термодинамических процессов всегда сопровождаются диссипацией (рассеянием энергии).

Принцип Онзагера

Поток 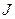всегда зависит от силы .

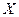Отражая функциональную зависимость, предположим, что:

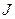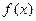= или .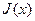

Функцию всегда можно разложить в ряд Маклорена вблизи равновесия (когда 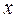=0),

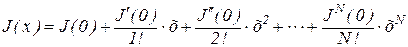
Ограничиваясь вторым слагаемым ряда (членами высшего порядка можно пренебречь) и считая, что x= 0 – отражает точку равновесия в ней, с учетом того, что вблизи равновесия J(0)=0 и, обозначив J¹(0)=L, получим:

= .

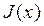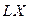Таким образом вблизи равновесия, возможна линейная связь между потоком и силой (поэтому эту термодинамику называют линейной), а коэффициент L – феноменологическим коэффициентом.

В любой биологической системе постоянно протекают множество процессов, каждый под действием своей силы Х.

Для простоты рассмотрим два процесса:

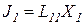, и ,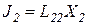

Естественно, что они влияют друг на друга:

,

.

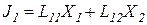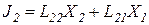Онзагер применил принцип взаимности, который в линейной термодинамике гласит, что 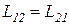, а так как 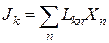, тогда и .

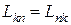Если подставить это уравнение в формулу диссипативной функции, получим основное феноменологическое уравнение линейной неравновесной термодинамики.

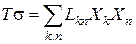
Теорема Пригожина

В теореме рассматривается основное свойство стационарного состояния, основной критерий его установления, связанный с состоянием энтропии.

Пусть в системе протекают два необратимых процесса:

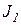и .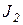

Локальная скорость продукция энтропии для этих процессов складывается из них:

.

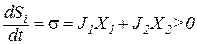Два сопряженных потока (пусть теплоты и вещества) взаимодействуют через коэффициенты:

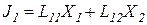– поток теплоты,

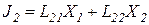– поток вещества.

Тогда с учетом принципа Онзагера / /: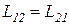

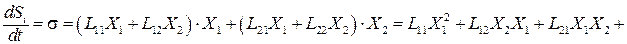
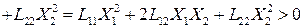
Теперь исследуем на экстремум величину s в стационарном состоянии (поток вещества 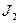=0). Для этого находим частную производную от s по 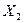при :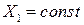

.

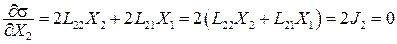Так как в стационарном состоянии все потоки равны нулю, исследуемая функция имеет экстремум.

Для проверки ее на знак берем вторую производную от s по 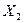при 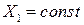и она равна ,

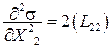а с учетом того, что все коэффициенты L больше нуля, то это минимум.

Таким образом, функция, которая всегда 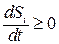, имеет минимум.

Теорема Пригожина утверждает, что скорость продукции энтропии внутри открытой системы в стационарном состоянии положительна и минимальна.

Она характеризует эволюцию открытой системы вблизи равновесия.

Следствие теоремы Пригожина.

Принцип Ле-Шателье.Если термодинамическую систему вывести из состояния равновесия, в ней возникнут силы и потоки, стремящиеся вернуть систему в исходное состояние равновесия.

Нелинейная термодинамика необратимых процессов.

Многие процессы протекают вдали от состояния равновесия, когда отсутствуют линейные связи между скоростями и силами.

Пригожин и Виам создали общую термодинамическую теорию роста и развития организмов.

Основное её положение заключается в следующем:

Развитие и рост организмов всегда происходит в направлении достижения стационарного состояния, что сопровождается уменьшением скорости продукции энтропии. То есть в линейной термодинамике основным всё же является утверждение: 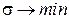, что определяет состояние системы

В нелинейной термодинамике продукция энтропии состоит из двух составляющих:

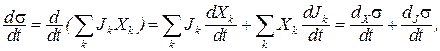
при постоянстве потоков 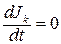и .

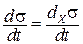Таким образом, основное неравенство нелинейной термодинамики: 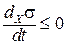отражает универсальный эволюционный критерий открытой системы вдали от равновесия. Условие устойчивости отражают флуктуации системы.

Флуктуации 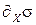могут быть как положительными: 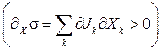, так и отрицательными: .

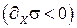В стационарном состоянии положительные флуктуации быстро исчезают за счет стремления скорости продукции энтропии к минимуму.

Отрицательные флуктуации являются следствием неустойчивости стационарного состояния системы и приведут к стационарному состоянию с уменьшенной энтропией (это эволюция).

В индивидуальном развитии организма есть три такие стадии:

– оогенез;

– регенерация;

– злокачественный рост.