Раздел 2. Молекулярная физика и термодинамика
Основные понятия молекулярно-кинетической теории (МКТ) и термодинамики. Опытные законы идеального газа.
Механика имеет дело с отдельными телами (обычно описывает движение не более трех тел). Молекулярная физика изучает системы, состоящие из огромного числа N~(NA=6,02×1023 моль-1) непрерывно хаотически движущихся частиц.
Исследовать процессы в таких системах с помощью законов механики практически невозможно. Однако молекулярная физика и термодинамика выработали свои особые методы изучения таких систем. Существует два общих подхода (метода):
- статистический – основывается на квантовой теории строения вещества и использует новые – статистические – закономерности, проявляющиеся только в коллективном поведении частиц системы; оперирует характеристиками отдельных частиц (скорость, энергия), используя их усреднение (наиболее вероятные значения) для описания всей системы;
- термодинамический (ТД) – изучает общие свойства макросистем (не вдаваясь в строение, происходящее внутри), находящихся в состоянии термодинамического равновесия; устанавливает соотношения между макропараметрами: обычно Р (давлением), V (объемом) и T (температурой) системы на основе обобщения большого числа опытных данных. Поэтому термодинамику часто называют феноменологической (от греч. «являющееся») теорией.
Оба подхода тесно связаны и хорошо дополняют, а в ряде случаев дублируют друг друга.
Дадим ряд определений.
Термодинамической системой (ТДС) называют мысленно выделенную совокупность тел (макросистему), которая рассматривается на основе ТД подхода. Открытая ТДС –ТДС, обменивающаяся с окружающей средой веществом и энергией, закрытая– только энергией. Напротив, изолированная ТДС (или замкнутая ТДС) – ТДС, не способная к обмену веществом и энергией с окружающей средой (идеальный случай, т.к. энергия может излучаться и поглощаться без соприкосновения изолированных тел, для замкнутой имеется ввиду неспособность обмениваться энергией через совершение механической работы). Адиабатная ТДС – замкнутая ТДС, не способная к обмену энергией с окружающей средой посредством теплообмена (реальные теплоизолированные системы с малым рассеянием теплоты).
ТД параметры делятся: на интенсивные, не зависящие от количества вещества в ТДС (P, T), и экстенсивные, зависящие и пропорциональные ему (V); на внешние, зависящие от положения и свойств внешних по отношению к ТДС тел (например, стенок сосуда – V), и внутренние, зависящие еще и от координат и скоростей частиц самой системы (Р, энергия).
В 1866г. австрийский физик Л.Больцман (1844–1906), будучи студентом, доказал, что величиной, характеризующей состояние ТДС независимо от ее микроскопической структуры, может быть средняя кинетическая энергия поступательного движения одной молекулы:
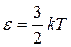 , (9.1)
, (9.1)
где k – постоянная Больцмана, k=1,38×10-23 Дж/К; Т – термодинамическая температура (по шкале Кельвина (англ. У. Томсон (1824–1907), за научные заслуги лорд Кельвин)) – мера кинетической энергии (теплового движения) частиц вещества. В настоящее время в международной практике, наряду с термодинамической шкалой, принято использовать международную практическую шкалу Цельсия (швед. A. Celsius (1701–1744)) Т=[t(°C)+273,15°]К. Считается, что при T=0 K – «нуль кельвин» – прекращается всякое движение. Такая температура не достижима, хотя возможно сколь угодно близкое приближение к ней.
ТД равновесием называется состояние системы, характеризующееся при постоянных внешних условиях неизменностью параметров (P,V,T) и отсутствием потоков вещества и энергии в системе.
Равновесное состояние системы характеризуется следующими свойствами:
1) оно не зависит от предыстории системы (от предшествующих состояний);
2) переход системы в равновесное состояние необратим;
3) в равновесном состоянии реализуется определенное стационарное (не зависящее от времени) распределение молекул по скоростям.
ТД процессом называется любое изменение состояния системы, связанное с изменением хотя бы одного термодинамического параметра. ТД процесс называется равновесным, если изменение состояния ТДС происходит при t®¥ (время), т.е. каждое предыдущее состояние характеризуется мало отличающимися от последующего ТД параметрами (P,V,T). Реальные процессы имеют конечную скорость (время) протекания и не являются равновесными, но могут быть приближенными к ним – квазиравновесными.
Модель идеального газа (ИГ) основывается на трех допущениях:
– собственный объем молекул пренебрежимо мал по сравнению с объемом сосуда;
– силы взаимодействия между молекулами отсутствуют;
– столкновение молекул друг с другом и со стенками сосуда в процессе хаотического теплового движения носит упругий характер.
Модель ИГ с успехом применяется для описания реальных газов при нормальных условиях (н.у.): P0=101325 Па=760 мм.рт.ст., Т0=273,15 К, а также при высоких температурах и низких давлениях. При иных условиях от уравнения ИГ можно перейти к теории реальных газов, вводя в эти уравнения поправки, учитывающие собственный объем молекул и силы взаимодействия между ними.
Простейшие примеры ТД процессов – изопроцессы (постоянной остается масса газа m=const и один из ТД параметров P, V или T). Они описываются экспериментально установленными законами:
а) изотермический (m=const, T=const) (рис.9.1, а) закон Бойля–Мариотта (англ. Р. Бойль (1627–1691), фр. Э. Мариотт (1620–1684)):
PV=const; (9.2)
б) изобарный(m=const, P=const) (рис. 9.1, б) закон Ж.Л. Гей-Люссака (1778–1850):
V=V0(1+a×t). (9.3)
При н.у. (Р0 и Т0) a=1/273,15 K-1;
в) изохорный(m=const, V=const) (рис. 9.1, в) закон Ж.Л. Гей-Люссака (1778–1850):
P=P0(1+a×t). (9.4)
Выражая время t через температуру T законы Гей-Люссака можно переписать в виде:
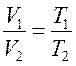 и
и 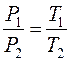 . (9.5)
. (9.5)
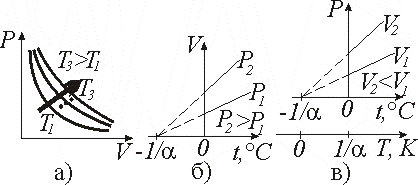
Рис. 9.1
Закон А. Авогадро (1776–1856): 1 моль любых газов при одинаковых температуре и давлении занимают одинаковый объем.
При н.у. молярный объем Vm=22,41×10-3 м3 (22,41 литра), а число частиц в одном моле любого газа NA=6,02×1023 моль-1.
Закон Дж. Дальтона (1766–1844): давление смеси газов равно сумме парциальных давлений газов, входящих в эту смесь: 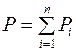 .
.
Парциальное давление – то, которое производил бы газ, входящий в состав смеси, если бы занимал сам весь объем, занимаемый смесью.
2.2. Уравнение Менделеева–Клайперона и основное уравнение МКТ
Уравнением состояния или термическим уравнением состояния называется функция f(P,V,T)=0, связывающая все макропараметры системы (ИГ). Получают его, следуя Б.П.Э. Клайперону (1799–1864) и Д.И. Менделееву (1834–1907 гг.).
Изменение состояния ИГ в результате двух изопроцессов (сначала изотермического, а затем изохорного), изображено на рис. 9.2.
Соответственно получают: P1V1=P'1V2 и 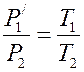 . Исключая из уравнений величину P'1, получают уравнение Клапейрона:
. Исключая из уравнений величину P'1, получают уравнение Клапейрона:
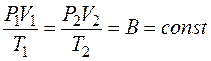 . (9.6)
. (9.6)
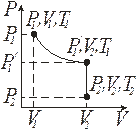
Рис. 9.2
Так как все состояния ИГ были выбраны произвольно, то уравнение (9.6) выполняется в любом ТД процессе для данной массы m ИГ (значение постоянной В зависит от природы газа).
Менделеев объединил уравнение Клапейрона с законом Авогадро. Так как при данных давлении и температуре газы занимают одинаковый объем, для одного моля газа можно записать:
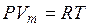 , (9.7)
, (9.7)
где R– универсальная газовая постоянная, не зависящая от природы ИГ R=k×NA=8,31 Дж/(моль×К).
Чтобы перейти к произвольной массе газа, заметим, что объем, который занимают v молей газа в v раз больше молярного объема Vm, т.е. V=nVm (по пропорции 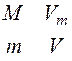 (М – масса одного моля (молярная масса) газа) с учетом n=m/M получают то же V=nVm). Тогда
(М – масса одного моля (молярная масса) газа) с учетом n=m/M получают то же V=nVm). Тогда
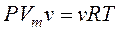 (9.8)
(9.8)
или
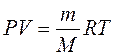 . (9.8')
. (9.8')
Иногда уравнение (9.8) записывают в виде
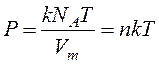 , (9.9)
, (9.9)
где n – концентрация частиц вещества (атомов, молекул).
В рамках модели ИГ получим основное уравнение МКТ, связывающее давление газа с механическими характеристиками молекул – скоростью и энергией.
Молекулы газа движутся с различными скоростями, поэтому для упрощения используют квадратичное усреднение 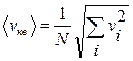 :
:
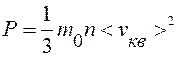 . (9.11)
. (9.11)
Уравнение (9.11) – основное уравнение МКТ. Учитывая, что n=N/V, уравнение (9.11) можно записать в виде:
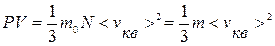 или
или 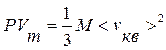 . (9.12)
. (9.12)
С учетом уравнения (9.7) получают
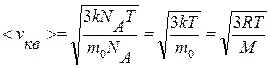 . (9.13)
. (9.13)
Для воздуха ( 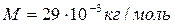 )
) 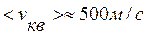 .
.
Средняя кинетическая энергия поступательного движения одной молекулы:
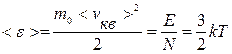 . (9.14)
. (9.14)
С учетом уравнения (9.14) основное уравнение МКТ можно записать в следующем виде:
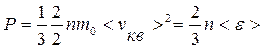 . (9.15)
. (9.15)
При Т=0 К поступательное движение молекул прекращается и газ не оказывает давления на сосуд.
Дата добавления: 2015-05-05; просмотров: 2400;
