Поле тяготения.

Издревле человек пытался ответить на вопросы: кто он, для чего он, как устроен он и окружающий его мир? Эти вопросы остаются актуальными и по сегодняшний день, хотя человек приобрел довольно много знаний об устройстве Вселенной. Процесс познания не всегда протекал спокойно и эволюционно. Например, смена господствовавшей более 1350 лет геоцентрической или птолемеевой (К. Птолемей (II в. н.э.)) системы мира (Земля – центр Вселенной, всё вращается вокруг нее) на гелиоцентрическую(современную: Солнце – одна из звезд, а планеты, в т.ч. и Земля, вращаются вокруг него)систему мира Н. Коперника (1473–1543) противоречила интересам католической церкви (ее догматам). Н.Коперник под страхом пыток и смертной казни публично отрекся от своей системы. Труд Н.Коперника «Об обращении небесных сфер» был под запретом Папы Римского вплоть до 1835г. Тем не менее истина нашла себе дорогу, и уже к XVII веку гелиоцентрическая система мира была признана большинством ученых.

В начале XVII века И. Кеплер (1571–1630) на основе собственных наблюдений и 35-летних наблюдений Т.Браге (1546–1601) сформулировал три закона движения планет:

I. Современная формулировка: при невозмущенном движении (задача двух тел) орбита движущейся материальной точки (небесного тела, в т.ч. и планеты) есть кривая второго порядка, в одном из фокусов которой находится Солнце, т.е. орбита материальной точки при невозмущенном движении – одно из конических сечений (окружность, эллипс (для планет), парабола, гипербола). Формулировка И. Кеплера (1609г., труд «Новая астрономия»): каждая планета движется по эллипсу в одном из фокусов которого находится Солнце.

II. Современная формулировка: при невозмущенном движении площадь, описываемая радиусом-вектором движущейся точки, изменяется пропорционально времени (закон площадей). Формулировка И. Кеплера (II и III законы опубликованы в 1619г., труд «Гармония мира»): радиус-вектор планеты за равные промежутки времени описывает равные площади.

III. Современная формулировка: при невозмущенном эллиптическом движении двух материальных точек (планет) вокруг центрального тела (Солнца (m₀)) произведения квадратов времен обращения на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит (III закон относится уже не к одной планете, а к Солнечной системе,рис.5.1):

,

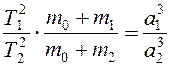при m₀>>m_i:

.

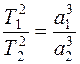Формулировка И. Кеплера: квадраты времен обращения планет относятся как кубы больших полуосей их эллиптических орбит:

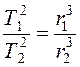. (5.1)

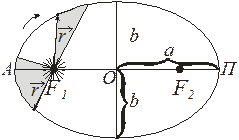
Рис. 5.1

Для описания взаимодействия тел на расстоянии (концепция близкодействия: все взаимодействия в природе характеризуются конечной скоростью передачи) пользуются понятием силового поля, т.е. считают, что тело изменяет свойства окружающего его пространства, а другое тело это «чувствует». Полю приписывается роль передатчика взаимодействия, энергии, его считают одной из форм существования материи(показанная А.Эйнштейном (1879–1955) в его теории относительности взаимосвязь массы и энергии (E=mc²) позволяет это утверждать).

Попытки создать единую теорию поля, объясняющую все известные явления с единой точки зрения, пока не увенчались успехом.

Поле называется силовым, если в каждой точке рассматриваемого пространства определен вектор 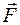силы любой природы происхождения.

Силовое поле (СП) называется однородным, если в любой его точке на тело действует одинаковая по модулю и направлению сила (любое поле в малой окрестности тела (точки) можно считать однородным).

Силовое поле называется центральным, если на тело, помещенное в поле, действует сила, всегда направленная вдоль луча, соединяющего тело (точку) и центр СП (полюс), а величина силы зависит только от расстояния от тела до центра поля. Примером такого поля может служить гравитационное поле, так как сила тяготения, согласно закону всемирного тяготения (И.Ньютон, 1687г., труд «Математические начала натуральной философии») равна

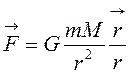, (5.4)

где r – расстояние между центрами взаимодействующих тел массами m и M. G – гравитационная постоянная, .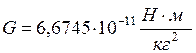

Силовой характеристикой любого силового поля является напряженность. Для гравитационного поля напряженность определяется по формуле

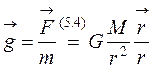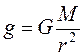, . (5.5)

Зная напряженность поля, мы можем определить силу, действующую со стороны поля на любое другое тело: 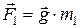. На поверхности Земли 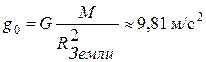в среднем. Так как планета Земля имеет форму слегка сплюснутого у полюсов шара, то эта величина изменяется (от 9,78 – на экваторе до 9,832 – на полюсах) в зависимости от места определения на планете (расстояния до центра планеты в этом месте).

Весом тела называется приложенная к телу сила 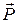, равная силе, с которой это тело действует на опору или подвес.При этом предполагается, что опора или подвес покоятся в системе отсчета, в которой взвешивают тело. В среднем 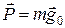, в общем случае, вес – есть геометрическая сумма силы гравитационного притяжения Земли и центробежной силы инерции, вызванной ее вращением.

При ускоренном движении системы могут возникнуть особые состояния, называемые перегрузками и невесомостью.

Вспомним известную со школы задачу о лифте (рис.5.11). При сонаправленности ускорения движения лифта 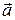и ускорения свободного падения 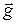вес тела P=N=m(g-a), т.е., если лифт движется с ускорением a=g, то Р=0. Это состояние называют невесомостью. Если же ускорения противонаправлены, то P=N=m(g+a). Увеличение веса приводит кперегрузкам.

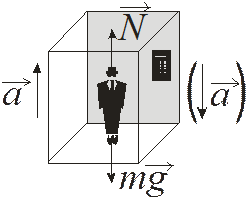
Рис. 5.11

Тяжелые перегрузки и невесомость в повседневной жизни – состояния редкие (быстрая езда в транспорте, полет на самолете, катание на качелях, подъемы и спуски в лифтах), с ними часто приходится сталкиваться лишь космонавтам, которых специально тренируют на центрифугах и в бассейнах для привыкания к состояниям деформации внутренних органов и изменениям внутреннего давления. В космических кораблях невесомость (движение с ускорением свободного падения) может быть компенсирована путем создания вращения корабля (действием сил инерции), при этом предметы вновь обретут вес, который будет зависеть от скорости вращения.

Гравитационное поле является потенциальным, т.е. его работа на замкнутом участке пути равна нулю:

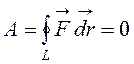(5.11)

Найдем работу силы тяжести при выполнении самолетом замкнутой фигуры пилотажа (рис. 5.3). Будем считать, что высота подъема над поверхностью Земли мала по сравнению с радиусом Земли, т.е. сила тяжести, как центральная сила, в любой точке траектории будет направлена к центру Земли (вниз), постоянна и равна 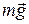(см. (3.2)).

При движении самолета работа совершается лишь на вертикальных участках траектории ( _^1, _^2, т.д.), на горизонтальных же участках ( _^1, _^2, т.д.) перемещение перпендикулярно линии действия силы и сила тяжести работы не совершает (3.1). Таким образом, работа силы тяжести определяется лишь разностью Dh высот в точках Н и О.

При подъеме самолета S из нижней точки О в верхнюю точку Н траектории направления действия силы и перемещения противоположны (работа отрицательна: –mgDh), а при последующем спуске совпадают (работа положительна: +mgDh), т.е. сумма этих работ дает нуль.

Для Земли 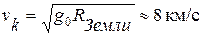– первая космическая скорость – скорость, которую надо сообщить телу, чтобы оно стало искусственным спутником Земли.

При параболическом движении (Е=0) имеют для Земли: 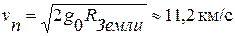– вторая космическая скорость – скорость, которую надо сообщить телу, чтобы оно стало искусственным спутником Солнца.

При сообщении телу третьей космической скорости n_г оно, тело, без действия дополнительных сил преодолеет притяжение Земли и Солнца и покинет пределы Солнечной системы (по гиперболе). Так как скорость Земли на орбите при движении вокруг Солнца ≈29,8 км/с, чтобы тело покинуло Солнечную систему, ему нужна скорость 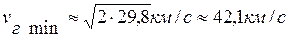, реально же еще большая, т.к. необходимо преодолеть земное притяжение. Причем эта скорость минимальна, если ориентирована по направлению орбитального движения Земли, и максимальна – если противонаправлена. Также необходим учет положения Земли на орбите (дальняя ли точка от Солнца – перигелий (П, см. рис. 5.1), ближайшая ли – афелий (А), положение других планет и звезд): n_г≈16,7¸72,7 км/с.

Четвертой космической скоростью называется скорость, которую необходимо сообщить телу, чтобы оно упало в заданной точке Солнца (n₄≈29,2¸31,8 км/с) или чтобы тело покинуло нашу Галактику (Млечный Путь) и ушло во Вселенную (тогда n₄³285 км/с).