Характеристики компонентов раствора.

Свойства раствора характеризуются значениями термодинамических функций H, U, F, G и т. д. Вследствие взаимодействия между молекулами компонентов раствора термодинамические характеристики имеет смысл относить к раствору как к целому, а не к составляющим его веществам. Однако все же важно оценить, какую долю вносит каждый компонент в то или иное свойство раствора. Такая характеристика называется парциальной величиной.

Большинство свойств, поддающихся количественному выражению, может быть разделено на две группы: экстенсивные и интенсивные.

Экстенсивные свойства пропорциональны количеству вещества. К ним относятся, например, заряд, объем, масса, внутренняя энергия, энтропия. Эти свойства системы накапливаются (обладают аддитивностью).

Такие свойства, точнее характеристики свойств, как температура, давление, потенциал, не зависящие от количества вещества, называются интенсивными. Интенсивные свойства различных частей системы стремятся к выравниванию.

Любое экстенсивное свойство раствора (x) зависит от условий его существования и состава:

x = f (P, T, n₁, n₂, ...), (7.23)

где Р - давление;

Т - температура;

n₁, n₂, ... - количества компонентов раствора.

Если в условиях Р, Т = const бесконечно мало изменить количества компонентов раствора, то изменение экстенсивного свойства можно определить по правилу нахождения полного дифференциала функции:

, (7.24)

где 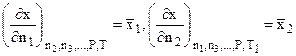и т.д.

В общем случае:

, (7.25)

где - парциальная молярная характеристика i-го компонента раствора (Г. Н. Льюис).

Таким образом, парциальная молярная характеристика компонента раствора - частная производная от какого-либо экстенсивного свойства раствора по числу молей этого компонента при условии Р, Т = const.

Учитывая (7.25), уравнение (7.24) перепишется в виде:

. (7.26)

В (7.26) dx - приращение любого экстенсивного свойства раствора при добавлении к нему dn₁, dn₂ и т. д. чисел молей компонентов раствора.

Величины 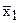, и т. д. показывают, на сколько изменяется экстенсивное свойство раствора (x) при добавлении к раствору 1 моля данного компонента, при условии, что количества других компонентов раствора останутся постоянными.

Интегрирование (7.26) приводит к уравнению вида:

, (7.27)

показывающее, что любое экстенсивное свойство раствора, например его объем, можно определить, зная состав раствора и парциальные молярные характеристики его компонентов.

Если одновременно изменять состав и количество раствора, то изменение (x) может быть найдено дифференцированием уравнения (7.27):

,

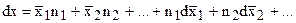где , поэтому

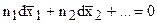, (7.28)

а после деления каждого из слагаемых на :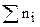

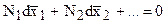, (7.29)

Уравнения (7.27), (7.28) и (7.29) - уравнения Гиббса - Дюгема, связывающие парциальные молярные характеристики компонентов раствора между собой.

Если в качестве экстенсивного свойства компонента раствора выбрать его объем, то парциальный молярный объем 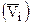определяется:

. (7.30)

Полный объем раствора рассчитывается с использованием (7.27):

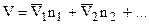. (7.31)

Парциальный молярный объем i-го компонента раствора 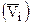может быть равен молярному объему i-го компонента (V_0i), что характерно для идеальных растворов. Такие растворы образуются без изменения объема раствора ( 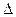V = 0):

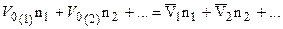. (7.32)

Образование реального раствора сопровождается изменением объема ( ), а его объем рассчитывается в соответствии с (7.27).

Для случая образования регулярных растворов .