Обратимые и необратимые процессы.

Подобно тому, как в первом начале термодинамики вводится функция состояния – внутренняя энергия, во втором начале – функция состояния, получившая название энтропия (S) (от греческого entropia – поворот, превращение). Рассмотрение изменения этой функции привело к разделению всех процессов на две группы: обратимые и необратимые (самопроизвольные) процессы.

Процесс называется обратимым, если его можно провести сначала в прямом, а затем в обратном направлении и так, что ни в системе, ни в окружающей среде не останется никаких изменений. Полностью обратимый процесс – абстракция, но многие процессы можно вести в таких условиях, чтобы их отклонение от обратимости было весьма мало. Для этого необходи мо, чтобы в каждой своей бесконечно малой стадии состояние системы, в которой этот процесс происходит, отвечало бы состоянию равновесия.

Состояние равновесия – особое состояние термодинамической системы, в которое она переходит в результате обратимого или необратимого процессов и может оставаться в нем бесконечно долго. Реальные процессы могут приближаться к обратимым, но для этого они должны совершаться медленно.

Процесс называется необратимым (естественным, спонтанным, самопроизвольным), если он сопровождается рассеянием энергии, т. е. равномерным распределением между всеми телами системы в результате процесса теплопередачи.

В качестве примеров необратимых процессов могут быть названы следующие:

- замерзание переохлажденной жидкости;

- расширение газа в вакуумированное пространство;

- диффузия в газовой фазе или в жидкости.

Систему, в которой произошел необратимый процесс, можно возвратить в исходное состояние, но для этого над системой нужно совершить работу.

К необратимым процессам относится большинство реальных процессов, так как они всегда сопровождаются работой против сил трения, в результате чего происходят бесполезные энергозатраты, сопровождающиеся рассеянием энергии.

Для иллюстрации понятий рассмотрим идеальный газ, находящийся в цилиндре под поршнем. Пусть начальное давление газа Р₁ при его объеме V₁ (рис. 4.1).

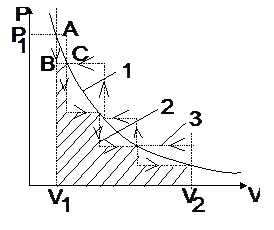Давление газа уравновешено насыпанным на поршень песком. Совокупность равновесных состояний описывается уравнением pV = const и графически изображается плавной кривой (1).

Если с поршня снять некоторое количество песка, то давление газа над поршнем резко снизится (от А до В) лишь после чего произойдет увеличение объема газа до равновесной величины (от В до С). Характер этого процесса – ломанная линия 2. Эта линия характеризует зависимость P=f (V) при необратимом процессе.

Из рисунка видно, что при обратимом расширении газа совершаемая им работа (площадь под плавной кривой 1) больше, чем при любом необратимом его расширении.

Таким образом, любой термодинамический процесс характеризуется максимально возможной величиной работы, если он совершается в обратимом режиме. К аналогичному выводу можно прийти, если рассмотреть процесс сжатия газа. Только следует иметь ввиду, что в этом случае величина работы – отрицательная величина (рис. 4.1, ломаная 3).