Коэффициент полезного действия тепловой машины. Цикл Карно.
Классический пример применения второго начала термодинамики – определение максимально возможного коэффициента полезного действия (К. П. Д.) тепловой машины. Исторически исследования в этой области послужили исходным пунктом термодинамики. Из положений второго начала следует, что тепловая машина должна содержать не менее двух тел, находящихся при разных температурах: нагревателя при температуре Т1 и холодильника при температуре Т2 (Т1>Т2). Для получения максимальной работы, перенос энергии от нагревателя к холодильнику должен осуществляться в обратимом режиме. Для осуществления переноса необходимо участие еще одного, так называемого рабочего тела, совершающего обратимый циклический процесс.
Отношение совершенной рабочим телом работы к сообщенной рабочему телу энергии – К.П.Д. тепловой машины ( 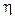 ):
):
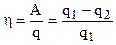 , (4.1)
, (4.1)
где А – совершенная рабочим телом полезная работа;
q1 – энергия, полученная рабочим телом от нагревателя в результате теплопередачи;
q2 – энергия, теплопередачей возвращенная рабочим телом холодильнику.
Схема тепловой машины может быть представлена рис. 4.2.
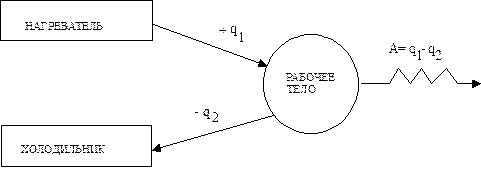
| Рис.4.2. Схема тепловой машины. |
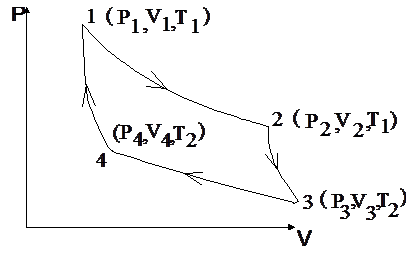 Пусть рабочий цикл тепловой машины состоит из двух изотерм (1 - 2 и 3 – 4) и двух адиабат (2 – 3 и 4 – 1). Такой цикл называется циклом Карно (рис. 4.3).
Пусть рабочий цикл тепловой машины состоит из двух изотерм (1 - 2 и 3 – 4) и двух адиабат (2 – 3 и 4 – 1). Такой цикл называется циклом Карно (рис. 4.3).
Все указанные на рис. 4.3 процессы являются обратимыми, поэтому исходное и конечное состояния газа совпадают. Рабочим телом является идеальный газ в количестве 1 моля, находящийся в цилиндре под поршнем.
| Рис. 4.3. Цикл Карно. |
Изотермическое расширение газа (1 –2) происходит в условиях контакта цилиндра с теплоотдатчиком (нагревателем), температура которого Т1. Газ расширяется до объема V2 и работа, им совершенная, равна поглощенной от нагревателя энергии:
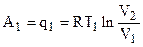 . (4.2)
. (4.2)
При адиабатическом расширении газа (2 – 3) цилиндр с поршнем отсоединяется от нагревателя и работа расширения газа выполняется за счет уменьшения его внутренней энергии:
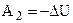 . (4.3)
. (4.3)
Изотермическое сжатие (3 – 4) газа происходит в условиях контакта цилиндра с холодильником (теплоприемником), а энергия, выделяющаяся при сжатии полностью поглощается холодильником:
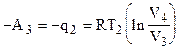 . (4.4)
. (4.4)
Работа, произведенная на последнем участке (4 – 1) цикла производится в условиях отсутствия контакта рабочего тела с холодильником и приводит к повышению запаса внутренней энергии газа и его температура увеличивается до Т2: 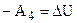 .
.
Суммарная величина работы, выполненная рабочим телом за цикл определяется:
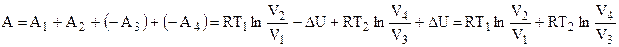 . (4.5)
. (4.5)
Из уравнений адиабат:
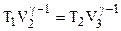 , (4.6)
, (4.6)
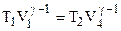 , (4.7)
, (4.7)
следует:
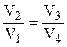 . (4.8)
. (4.8)
Следовательно (4.5) с учетом (4.8) примет вид:
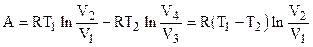 . (4.9)
. (4.9)
Тогда К. П. Д. вычисляется:
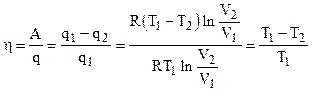 , (4.10)
, (4.10)
окончательно:
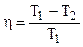 . (4.11)
. (4.11)
Соотношение (4.11), полученное для цикла Карно, можно рассматривать как аналитическое выражение второго начала термодинамики. Из (4.11) следует, что К. П. Д. тепловой машины зависит только от температур нагревателя и холодильника и он тем больше, чем ниже Т2.
Можно доказать, что К. П. Д. цикла Карно, состоящего из обратимых процессов, больше К.П.Д. любого другого цикла ( 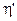 ), состоящего из нескольких обратимых процессов (теорема Карно):
), состоящего из нескольких обратимых процессов (теорема Карно):
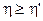 . (4.12)
. (4.12)
Высокое значение К. П. Д. цикла Карно является следствием не его специфической формы, а обратимостью всех его составляющих.
Из соотношения (4.12) следует:
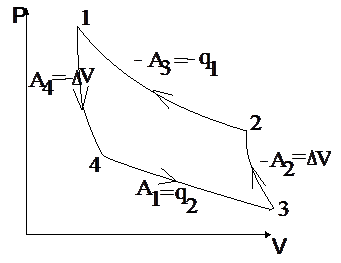
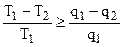 или
или 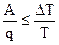 , (4.13)
, (4.13)
откуда:
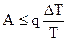 . (4.14)
. (4.14)
Неравенство (4.14) - одна из форм записи второго начала термодинамики.
Дата добавления: 2015-05-21; просмотров: 1390;
