Системи числення
Пакет Mathcad має можливість працювати з числами, які представлені в двійковій, вісімковій чи шістнадцятковій системах числення. Для зображень чисел в двійковій системі числення використовуються два символи: нуль та одиниця, в вісімковій системі числення використовуються символи від 0 до 7, а в шістнадцятковій – від 0 до 9 та A, B, C, D, E, F.
Для введення числа в двійковій системі числення відразу після числа без пропуску вказати літеру, яка ідентифікує систему числення. Так, для двійкової системи це літера b чи B, вісімкової – літера 0, а для шістнадцяткової – літера h чи H.
Щоб змінити систему числення в діалоговому вікні Rezult Format, треба відкрити закладку Display Options та з висувного списку вибрати один з елементів: Decimal(десяткова), Binary(двійкова), Octal(вісімкова) та Hexadecimal(шістнадцяткова).
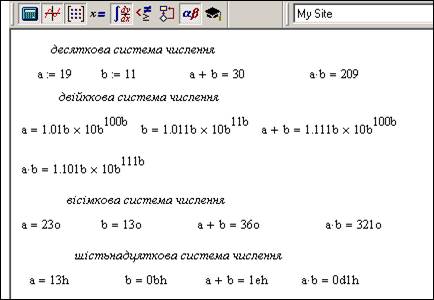
Рис.2.6. Значення чисел в різних системах числення
На рис.2.6 наведені значення чисел у різних системах числення. Слід відмітити, що при наборі чисел в шістнадцятковій системі числення число обов’язково повинно починатися з нуля, а далі без пропуску повинен вказуватись код шістнадцяткового числа, який закінчується літеро h. На рис 2.1 для кожної системи застосовується свій формат. Щоб налаштувати формат для окремого числа, необхідно його виокремити ти двічі клацнути на ньому мишею. При цьому відкривається діалогове вікно Rezult Format, в якому налаштування виконується, так як і для всього документа. Якщо при введенні ідентифікатора системи числення Mathcad автоматично вставити знак множення, то цей знак потрібно вам включити вручну, щоб правильно інтерпретувалось число.
2.5. Стандартні математичні функції
Mathcadмає доволі значний набір вбудованих математичних функцій, що значно розширює його можливості.
Щоб вставити вбудовану математичну функцію в документ, можна скористатися такими способами: ввести ім’я функції безпосередньо з клавіатури згідно з синтаксисом цієї функції або скористатися діалоговим вікном, в якому необхідно вибрати потрібну функцію. Очевидно, що другий спосіб більш зручний тому, що немає потреби в запам’ятовуванні точної назви функції, її аргумента чи аргументів. У діалоговому вікні можна одержати довідку стосовно вибраної функції.
Для відкриття діалогового вікна вставлення функції слід виконати команду Insert│Function або скористатися кнопкою на панелі інструментів, на якій зображений символ функції. Це вікно має два списки: Function Categoryта Function Name. Всі функції поділені на категорії, які і відображені в відповідному списку, а в списку Function Name наведений перелік функцій, які належать до цієї категорії.
Найбільш поширені вбудовані математичні функції, які використовуються при розв’язуванні інженерних задач наведені в таблиці 2.1
Таблиця 2.1. Основні математичні функції
| Функція | Опис |
| acos(z) acosh(z) arcot(z) acoth(z) acsc(z) acsch(z) asec(z) asin(z) asinh(z) atan(z) atanh(z) cos(z) cosh(z) cot(z) coth(z) csc(z) csch(z) exp(z) Im(z) Re(z) ln(z) log(z,b) sec(z) sech(z) sin(z) sinh(z) tan(z) tanh(z) | Арккосинус від Z Арккосинус гіперболічний від Z Арккотангенс від Z Арккотангенс гіперболічний від Z Арккосеканс від Z Арккосеканс гіперболічний від Z Арксеканс від Z Арксинус від Z Арксинус гіперболічний від Z Арктангенс від Z Арктангенс гіперболічний від Z Косинус від Z Косинус гіперболічний від Z Котангенс від Z Котангенс гіперболічний від Z Косеканс від Z Косеканс гіперболічний від Z Показникова функція Уявна частина комплексного числа Дійсна частина комплексного числа Логарифм натуральний від Z Логарифм від Z з основою b Секанс від Z Секанс гіперболічний від Z Синус від Z Синус гіперболічний від Z Тангенс від Z Тангенс гіперболічний від Z |
Група функцій Mathcad призначена для заокруглення та перетворення числових значень (наведена в табл.2). Ці функції відносяться до категорії Truncation and Round Offвікна Insert Function.
Таблиця 2.2 Функції перетворення значень
| Функція | Опис |
| Ceil(x,y) | Функція повертає значення, яке є найменше кратне числа y, але не менше від числа x. |
| ceil(x) | Функція повертає найменше ціле число, яке більше або рівне x. |
| Floor(x,y) | Повертає найбільше кратне y, що не перевищує x. |
| floor(x) | Значення функції є найбільше ціле число, яке не перевищує x. |
| Round(x,y) | Значення x заокруглюється до найменшого числа, яке кратне числу y. Функцією повертається значення, при цьому значення змінної х не змінюється. |
| round(x,n) | Число х заокруглюється до n знаків після десяткової крапки. Якщо аргумент n не вказаний, то заокруглення відбувається до цілочислового значення. |
| Trunc(x,y) | Функція повертає значення, яке є результатом множення аргумента y на цілу частину від ділення аргумента х на аргумент у. |
| trunc(x) | Функція повертає цілу частину числа х. |
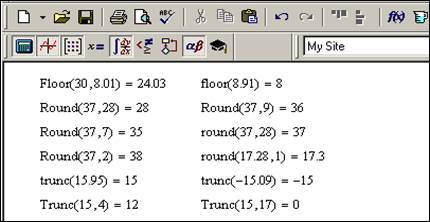
Рис.2.7. Функції користувача
Функція, яку створює користувач, складається з імені функції, в дужках записуються аргументи, далі слідує знак присвоєння та вираз. Аргументів в функції може бути декілька, тоді вони записуються через кому. Вираз має містити аргументи функції та інші змінні, які попередньо мають бути визначені. Щоб довідатись числове значення функції для конкретного аргумента, функція викликається з цим аргументом та після неї ставиться знак рівності.
На рис.2.8 наведені приклади створення функцій та обчислення її значень.

Рис.2.8. Обчислення значень функції
В Mathcadзмінній можна присвоювати не тільки числа, але й діапазон значень змінної. Змінні, яким присвоюється діапазон значень, називають ранжованими змінними. Ранжовані змінні мають послідовність фіксованих значень у вигляді цілих або дійсних чисел, які змінюються з певним кроком від початкового значення (Nbegin) до кінцевого (Nend) з кроком зміни (Step), тобто:
Name:=Nbegin, Nbegin+Step..Nend(2.1)
Якщо початкове значення змінної, Nbegin, є меншим за її кінцеве значення змінної, Nend, то значення кроку Step має бути додатним, в протилежному випадку крок є від’ємним.
Якщо крок зміни рівний одиниці, то для створення ранжованої змінної використовується вираз:
Name:=Nbegin.. Nend(2.2)
При цьому, якщо Nbegin<Nend, то крок зміни рівний +1, і якщо Nbegin>Nend, то крок „мінус” 1. У цьому операторі дві крапки вводяться натисненням клавіші <;> – якщо просто ввести з клавіатури дві крапки, то вони інтерпретуються як десяткові і з’являється повідомлення про помилку.
При введенні значень-діапазонів можна скористатися палітрою Matrix, на якій є спеціальна піктограма для введення діапазонних значень.
На рис.2.9 наведений приклад обчислення значень функції з використанням ранжованої змінної.
Якщо функція має декілька аргументів, які набувають значення – діапазону, тоді обчислення виконуються так: при фіксованих решті аргументів перший вибирає всі значення з діапазону, після чого на величину кроку змінюється друга змінна, а перша знову вибирає всі значення, починаючи з початкового. Коли весь діапазон вибирає друга змінна, на величину кроку змінюється третя змінна і т. д. Так на рис.2.10 показано обчислення значень функції двох змінних.
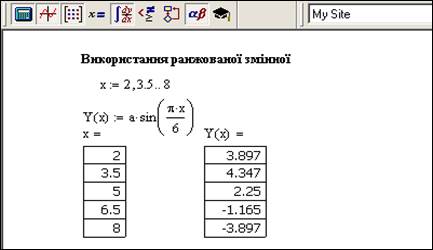
Рис.2.9. Використання ранжованої змінної
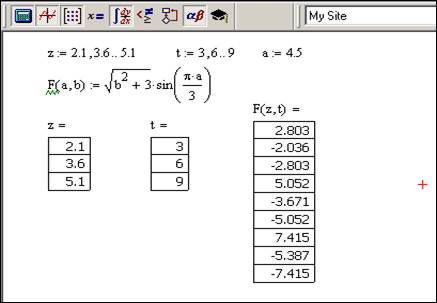
Рис.2.10. Обчислення значеннь функції двох змінних
Список значень функцій (аргументів) може бути достатньо великим, і тоді він відображається не весь. Щоб переглянути всі значення, необхідно виокремити цей список в області відображення значень, при цьому з’являється смуга прокрутки. Користуючись нею, можна переглянути весь список значень. Можна також змінити розміри частини списку. Для цього потрібно виокремити цей список та навести курсор на рамку виокремлення в те місце, де є чорна вузлова крапка, та перемістити границі списку в потрібному напрямі.
Дата добавления: 2015-05-19; просмотров: 1866;
