Введення тексту
У будь-яке місце робочого аркуша можна вставляти текст. Для цього потрібно вставити курсор у потрібне місце та набрати на символ подвійних лапок <”>, або виконати команду Insert│Text. Після цього буде утворена текстова область, в яку вводять текст. При наборі тексту область збільшується. Після введення тексту потрібно клацнути за межами прямокутника. Перед набором тексту можна вибрати шрифт, розмір символів та тип шрифту. При форматуванні тексту його слід виокремити та скористатися командою Format│Text, при цьому відкривається вікно, де можна вибрати параметри форматування.
2.7. Редагування виразів
При створенні робочого документа часто виникає потреба внести правки в певному місці, зокрема:
при вставленні оператора він розміщується після того виразу, який виокремлений лініями редагування, якщо вираз знаходиться ліворуч від вертикальної лінії редагування ;
переміщувати вертикальну лінію редагування з початку виразу в кінець та навпаки можна з допомогою клавіші <Ins>;
при вилученні бінарних операторів, замість них, часто відображається позначка у вигляді прямокутника . Це свідчить про те, що в цьому місці повинен бути введений оператор;
для того, щоб вираз(підвираз) взяти в дужки, потрібно скористатись клавішею <’>. При цьому все, що було виокремлено лініями редагування, береться в дужки;
при вилученні однієї дужки автоматично вилучається її пара;
щоб вказати введений вираз як аргумент функції, необхідно його виокремити та взяти в дужки (клавіша <’>), вертикальну лінію редагування перевести ліворуч від виразу та ввести назву функції.
Питання для самоконтролю
1. Дайте визначення математичного виразу.
2. Яке призначення палітри Calculator?
3. Перелічіть операції, що застосовуються при побудові математичного виразу?
4. Як виокремити частину математичного виразу?
5. Як ввести математичний вираз, який містить чисельник та знаменник?
6. Яка різниця між знаками операторів: :=, =,≡ ?
7. Як налаштувати зображення оператора присвоєння?
8. Що означає локальна та глобальна ініціалізація змінних?
9. Які є параметри форматування даних?
10. Які є типи числових форматів? Як змінити формати змінних?
11. Яка різниця між інженерним та науковим форматами змінних?
12. Наведіть приклади використання дробового формату чисел.
13. Як представляються числа в двійковій, вісімковій та шістнадцятковій системах числення?
14. Як представляються комплексні числа?
15. Як вставити вбудовану функцію у вираз, використавши вікно Insert Function?
16. Яка різниця між функціями Round(x,y) та round(x,n)?
17. Яка різниця між функціями Trunc(x,y) та trunc(x)?
18. Як побудувати функцію користувача?
19. Як встановити значення–діапазон для змінної?
20. Наведіть приклад обчислення значень функцій двох змінних? Яка послідовність обчислення значень функцій двох змінних?
21. Як зменшити (збільшити) розміри списку значень на екрані?
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №1
Математичн і вирази. Обчислення значень функції
Мета роботи.Набути практичні навички із створення математичних виразів, їх редагування та форматування результатів обчислень.
Хід роботи
1. Обчислити два значення функції для початкового та кінцевого значень аргумента ,таблиця 1.
2. Представити результати обчислень п.1, в інженерному і науковому форматах та в десятковій,двійковій, вісімковій, шістнадцятковій системах численнях.
3. Виконати табуляцію функції згідно з даними наведеними в таблиці 1.
Таблиця 2.1- Варіанти завдань
| № ва- | Константи | Аргу- | Почат- кове знач. | Кінце- ве зна-чення | Крок зміни Пара- | Кіль- кість інтер- | ||
| рі- ан-ту | Функція | a | b | мент | пара-метра циклу | пара- метра циклу | Метра Циклу | валів пара- метра |
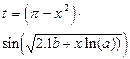
| 21.4 | 1.95 | x | 4.6 | - | 1.5 | ||
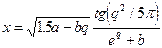
| 121.2 | 3.8 | q | 1.4 | 1.85 | - | ||
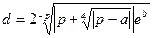
| 8.3 | 1.43 | p | - | -4.74 | 0.15 | ||
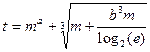
| 1.6 | 2.09 | m | - | 1.5 | |||
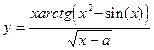
| 0.83 | - | x | 1.15 | - | 0.35 | ||
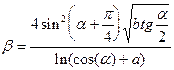
| 3.85 | 1.8 | a | - | 150 | 70 | ||
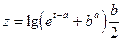
| 1.6 | 14.3 | t | 2.75 | 5.0 | - | ||
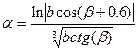
| - | 6.21 | b | 400 | 540 | - | ||
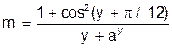
| 2.43 | - | y | 1.62 | - | 0.15 | ||
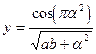
| 1.85 | 2.63 | a | -3.45 | - | -1.6 | ||
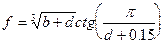
| - | 3.85 | d | -2.3 | 0.01 | - | ||
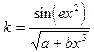
| 2.65 | 1.48 | x | 0.75 | 0.012 | - | ||
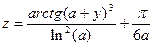
| 3.2 | - | y | -4.8 | 0.1 | - | ||
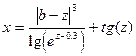
| - | 8.45 | z | - | 0.24 | 3.2 | ||
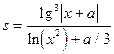
| -16.3 | - | x | -16.3 | - | -9.3 | ||
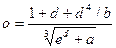
| -8.6 | 3.28 | d | 3.6 | - | 4.0 | ||
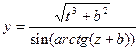
| 1.42 | 0.85 | z | 1.6 | 0.35 | - | ||

| 3.2 | - | f | -4.8 | 0.1 | - | ||
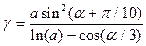
| 8.9 | - | a | 350 | - | 500 | ||
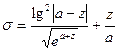
| 1.2 | - | z | 2.6 | - | 3.8 |
3. Графіка в Mathcad
3.1. Побудова графіків
При проведенні розрахунків чи проведенні експериментальних досліджень часто виникає потреба представити результати розрахунків чи експериментів у вигляді графіків, діаграм тощо.
Система Mathcad має широкі можливості для побудови графіків, як двовимірних (X-Y Plot, Polar Plot), так і тривимірних графіків (графіки типу 3D) чи діаграм.
3.2. Створення двовимірних графіків
Під двовимірним графіком розуміють відображення у графічному вигляді залежності функції від її аргументів. Вставлення графіка в документ виконується командою Insert | Graph | X-Y Plot, при цьому в документ вставляється область графіка, яка містить ряд структурних заповнювачів, рис.3.1.
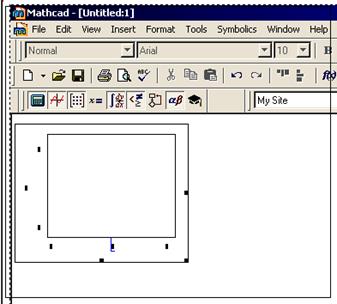
Рис.3.1. Область для відображення графіка
Замість заповнювача, що знаходиться в нижній частині графіка, потрібно ввести ім’я аргумента функції, а замість заповнювача, що знаходиться ліворуч області побудови графіка, ім’я функції, для якої будується графік або вираз, з допомогою якого обчислюються значення функції. На рис.3.2 аргумент функції вказаний Х,а ім’я функції, для якої будується графік, є cos(x). Тепер, якщо клацнути мишею за межами графіка, то з’явиться графік введеної функції.
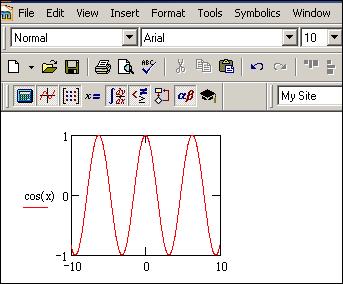
Рис.3.2. Графік косинусоїди
Якщо діапазон зміни аргумента не вказаний, то графік функції за замовчуванням будується в діапазоні від 10 до 10.
Значення функції, які відображаються по осі ординат, автоматично масштабуються так, щоб графік функції повністю розміщувався в області його відображення, – від мінімального до максимального значення функції. Крім того, користувач має можливість змінити відображення максимального та мінімального значення функції чи величину діапазону зміни аргумента функції. Для цього потрібно виокремити графік та ввести необхідні числові значення замість кутових заповнювачів, які розташовані біля координатних осей. Якщо графік уже створений і необхідно його відредагувати, то границі зміни значень функції чи (і) аргумента вводяться замість тих числових значень, які відображені на графіку.
При побудові графіка функції, крім виразу, за яким обчислюються її значення, на практиці задають і діапазон зміни аргумента. Тоді необхідно визначити діапазон зміни аргумента перед побудовою графіка функції. Так, на рис.3.3 показаний графік функції f(x)=cos(x)/x при зміні аргумента функціїХвід -11π/2 до 11π/2 з кроком 0.1. Очевидно, що перед визначенням діапазону аргумента, необхідно записати визначення функції через вираз. При цьому графік функції будується для значень аргумента, які належать діапазону його ініціалізації. Границі значення діапазону зміни аргумента функції відображаються під горизонтальною координатною осею при виокремленні графіка (рис.3.3).
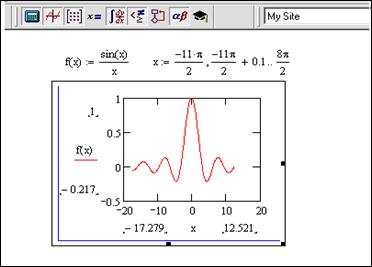
Рис.3.3. Використання ранжованої змінної
В деяких випадках доцільно побудувати на одному рисунку графіки декількох функцій. Для цього після введення імені однієї функції через кому необхідно ввести ім’я другої функції і так далі. Кома не виводиться, а ім’я другої функції та тип лінії другого графіка розташовується під іменем першої. Якщо функції мають різні імена аргументів, то внизу осі абсцис потрібно ввести їх імена через кому. Послідовність слідування зверху донизу імен функцій біля осі ординат графіка повинна відповідати послідовності аргументів функцій зліва направо. Кожна функція може мати свій діапазон зміни аргумента функції, що буде відображено при побудові графіків, рис.3.4.

Рис 3.4. Графіки двох функцій
3.3. Відображення значень масиву
Крім неперервних функціональних залежностей, в Mathcad на графіках можна представляти дискретні набори значень даних. Це можуть бути дані експерименту або елементи масиву.
При створенні відображень значень елементів масиву на графіку по вісі абсцис вказується індексна змінна, а по вісі ординат – назва елемента масиву (із зазначенням індекса в символьному вигляді). Очевидно, що масив попередньо має бути визначеним, а індексній змінній потрібно присвоїти значення – діапазон. Приклад наведений на рис.3.5.
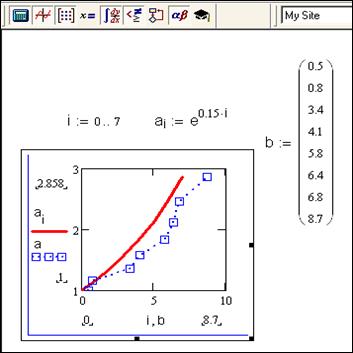
Рис.3.5. Побудова графіків одновимірних масивів
Часто буває так, що і абсциси, і ординати точок, які потрібно відобразити на графіку, є елементами масивів. Для побудови графіка необхідно коло горизонтальної вісі вказати назву масиву В, а біля вертикальної – масиву А.
3.4. Форматування графіків
З метою наглядного відображення графіка (графіків) їх форматують, тобто вибирають тип, колір та товщину ліній, встановлюють підписи та назви графіка, координатну сітку та ряд інших параметрів. Для виконання форматування необхідно виокремити графік та вибрати команду Format/Graph/X-Y Plot, цю ж команду можна активізувати, якщо двічі клацнути на графіку. При цьому відкривається діалогове вікно Formatting Currently Selected X-Y Plot. Це вікно має чотири закладки: X-Y Axes, Traces, Labelsта Defaults.На закладці X-Y Axes виконуються налаштування, які пов’язані з видом та типом координатної системи графіка. Там містяться три розділи: X-Axisта Primary Y Axis (Secondary Y Axis), рис.3.6. під назвами розділів розташовані групи перемикачів певних опцій. Опції в розділах X-Axis і Primary Y Axis (Secondary Y Axis)однакові, а різниця лише в тому, що налаштування стосується горизонтальної та вертикальної осей графіка. Так, опція Log Scale дозволяє встановлювати логарифмічний масштаб шкал, а опцію Grid Lines активізують тоді, коли потрібно відобразити координатну сітку.
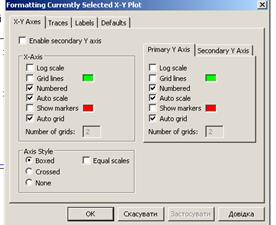
Рис.3.6.Вікно Formating Curently Select X-Y
Опція Numbered дозволяє встановлювати нумерацію позначок вздовж осей. Кількість позначок на осях встановлюється в полі Number of grids. Застосування показано на рис.3.6.
При активізації позначки Show markers є можливість встановити додаткові горизонтальні чи вертикальні лінії, при цьому з’являються по два структурних заповнювача біля кожної осі. Замість цих заповнювачів вводиться число, яке відповідною командою для проведення горизонтальної чи вертикальної лінії.
На рис.3.7 показана одна вертикальна лінія з координатою 5 і одна горизонтальна з координатою 3, числове значення координат цих ліній також виводиться на графіку. Для вилучення координатної лінії необхідно виокремити числове значення її координати та вилучити його.
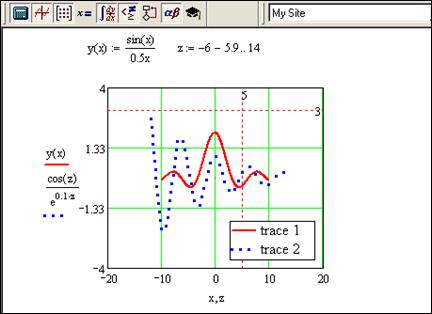
Рис.3.7. Відображення маркованих ліній
При активізації опції Auto grid число позначок вздовж координатних осей встановлюється автоматично. Опція Number of grids дозволяє користувачу встановити число інтервалів поділу значень вздовж відповідної осі, очевидно, що при цьому опція Auto grid має бути вимкнута.
Розділ Axis Style вікна форматування має три перемикачі (Boxed, Crossed і None) та опцію Equal Scales. Опція Boxed встановлена за замовчуванням і відповідає координатній системі, коли область графіка поміщена в прямокутну рамку. При ввімкненій опції Crossedкоординатні осі перетинаються на початку координат, якщо не відображати координатну сітку, то слід включити опцію None. Опція Equal Scales встановлює однакові масштаби для горизонтальної та вертикальної осей.
У вікні форматування графіка, рис 3.6, є кнопка Застосувати.Якщо клацнути на цій кнопці, то встановлені параметри форматування будуть застосовані для графіка, при цьому діалогове вікно не буде закрите і можна встановлювати інші параметри форматування. Якщо клацнути на кнопці OK, то вікно форматування закриється.
Щоб додаткова вертикальна вісь Secondary Y Axis, була доступна,потрібно активізувати опцію Enable Secondary Y Axis, при цьому в правій частині графіка з’являється структурний заповнювач, куди вводять ім’я та аргумент функції для побудови графіка.
На закладці Traces вікна Formatting Currently Selected X–Y Plot міститься налаштування, яке стосується способу відображення функціональних залежностей. У стовпці Legend Label відображаються позначки для легенд графіків, які є також індикаторами графіків функції. У списку Legend Label є шістнадцять елементів. Це означає, що одночасно на одному рисунку можна відобразити до шістнадцяти різних графіків. У стовпці Symbol вказується тип базового символу, з допомогою якого формуються криві для графіків (за замовчуванням відображається значення none), а в полі Symbol Frequency вибирається щільність символів на кривій, а розміри цих символів знаходяться в полях стовпця Symbol Weight. У стовпці Line можна вибрати один з чотирьох типів ліній (суцільна, пунктирна, штрихова, штрихпунктирна) для відображення графіків. Якщо графіків більше ніж чотири, то для них задають різні кольори в стовпці Color. Спосіб відображення графіків можна вибрати в стовпці Type, зокрема:
points – на графіку відображаються тільки базові точки;
bar –графік відображається у вигляді стовпців;
step –графік відображається у вигляді неперервної ступеневої функції тощо.
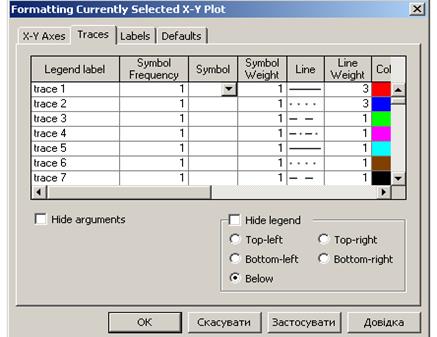
Рисунок 3.8. Вікно Formating Currently Select X-Y Рlоt
Різні графіки можна виокремити з допомогою ліній різної товщини чи стовпців різного розміру, скориставшись списком, який розташований під стовпцем Line Weightта Symbol Weight.Товщина задається в пікселях від 1 до 9. Останній стовпець Y - Axisвизначає тип вертикальної координатної осі.
Назва (легенда) графіка відображається в тій частині рисунка, що визначається положенням перемикача в розділі Hide Legend.Відповідність між застосуванням легенди та станом перемикачів така:
· Top – left– ліворуч вверху;
· Bottom – left– ліворуч внизу;
· Below– внизу;
· Top – right– праворуч вверху;
· Bottom – right– праворуч внизу.
Активізація опції Hide Argumentsдозволяє скрити назви аргументу та функції вздовж осей. У діалоговому вікні Formatting Currently Selected X–Y Plotє ще дві закладки Labels та Defaults.На закладці Labelsзадається заголовок графіка, а також підписи координатних осей. Текст заголовка вводиться в полі Title,а для його відображення потрібно активізувати опцію Show Title.Заголовок можна розмістити над (опція Above) чи під (опція Below) графіком. Аналогічно вводяться підписи осей Х - Axisчи Y - Axis (Y2 - Axis).
Закладка Defaultsмає дві опції. Активізація опції Change to Defaultsдозволяє повернути параметри налаштування графіків за замовчуванням, а опція User for Defaultsдозволяє використати встановлені параметри за замовчуванням для всіх графіків в документі.
3.5. Графіки в полярній системі координат
У полярній системі координат точка задається двома параметрами: віддаль rвід точки до початку системи координат та кута φміж горизонтальною віссю і лінією, яка з’єднує точку з початком координат .
Для прикладу побудуємо графік кривої, яка називається кривою Архімеда. Рівняння першої кривої r(φ) = a · φ, a = 3.Аргумент змінюється від 0 до 3/2πз кроком 0.2. Рівняння другої - r1(φ) = a1 · φ,тутa1 = 2.1.Аргумент за замовчуванням змінюється від 0 до 2π, рис 3.6.
Процедура побудови графіка в полярній системі координат аналогічна побудові графіка в декартові системі координат. Зокрема, потрібно виконати команду Insert | Graph | Polar Plotабо скористатися акордом клавіш <Ctrl> + <7>і в документ буде встановлена область побудови графіка, в центрі якого зображений круг, знизу та ліворуч розташовані два заповнювачі. Замість нижнього заповнювача, вказується аргумент функції, а заповнювач, що знаходиться ліворуч круга функції, замінюється на ім’я функції з її аргументом. Очевидно, функція має бути визначена. Вказується також діапазон зміни аргументу. Якщо діапазон зміни аргументу не вказаний, то за замовчуванням він встановлюється від 0 до 2π. Графіки, на яких зображена спіраль Архімеда, показані на рис. 3.9.
Форматування графіка в полярних координатах виконується в діалоговому вікні Formatting Currently Plotаналогічно форматуванню графіків типу X–Y Plot.
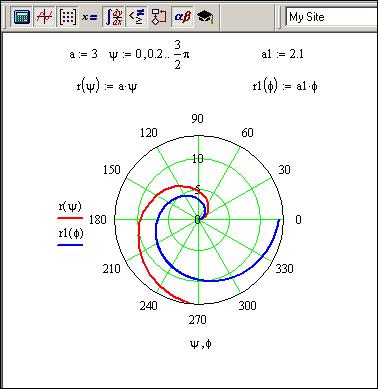
Рис.3.9.Графіки функцій в полярних координатах
3.6. Основні методи роботи з графіками
Mathcadмає можливість змінювати розміри рисунків з графіками. Для цього графік необхідно виокремити. Якщо є потреба змінити розміри рисунка зі збереженням пропорцій по висоті і ширині, то курсор встановлюють на праву нижню кутову точку області виокремлення рисунка. При натиснутій лівій клавіші миші переміщують курсор, задаючи необхідні розміри. Курсор при цьому має вигляд похиленої двосторонньої стрілки.
Якщо потрібно змінити лише висоту чи ширину, то курсор наводять на праву чи нижню точки в області виокремлення. Курсор приймає вигляд вертикальної або горизонтальної двосторонньої стрілки. При натиснутій лівій клавіші миші розтягують чи стискають рисунок в певному напрямі.
Для переміщення рисунку з графіком потрібно підвести курсор миші на границю області виокремлення, і він відобразиться у вигляді долоні руки. При натиснутій лівій клавіші миші переміщають рисунок у відповідне місце.
ВMathcad’іє можливість збільшувати не тільки весь графік, але й його частину. Це застосовується тоді, коли треба дослідити, як змінюється значення функції на графіку протягом малого проміжку часу. Для цього потрібно виокремити графік та викликати контекстне меню і з його списку вибрати елемент Zoom. Елемент Zoomможна вибрати також з меню View.При цьому відкривається діалогове вікно X – Y Zoom,яке має чотири поля та п’ять кнопок, рис 3.10.
Далі виокремлюють ту область графіка, яку необхідно збільшити (прямокутник з штрихових ліній). У полях діалового вікна X – Y Zoomвідображається найбільше (max) і найменше (min) значення координат XіYв даній області, рис. 3.7.
Для збільшення виділеної області потрібно клацнути на кнопці Zoom(кнопка зі зображенням лупи і знака плюс). Відмінити вилучення можна, скориставшись кнопкою Un zoom(кнопка з зображенням лупи та знака мінус). Для повернення в первинний режим графіка треба клацнути на кнопці Full View(кнопка із зображенням діагональних стрілок).
Коли необхідно дізнатися про числові значення координат точки графіка, необхідно виокремити графік, вибрати з контекстного меню (права клавіша) елемент Trace.При цьому відкривається діалогове вікно X – Y Trace,де є два поля, три кнопки та одна опція. Якщо тепер клацнути лівою клавішею в області графіка, то на ньому буде виокремлена точка, що є найближчою до точки розташування курсору (опція Track data Points має бути активна), і координати цієї точки відобразяться в полях вікна X – Valueта Y – Value, рис. 3.8. Значення ординати та абсциси можемо скопіювати, скориставшись кнопкамиCopy Xчи Copy Y.Якщо потрібно визначити координати точки, яка належить області відображення графіка, то потрібно відмінити опцію Track data Points.

Рис.3.10. Виокремлення області для подальшого збільшення
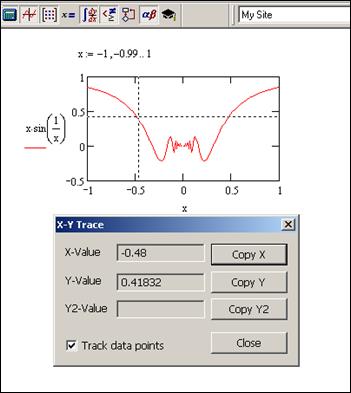
Рис.3.11. Визначення координат точок на графіку
3.7. Ствлорення тривимірних графіків
При побудові тривимірних графіків використовується та ж концепція, що і при роботі з двовимірними графіками, але сама процедура їх побудови є складнішою.
В Mathcad можна створювати такі типи тривимірних графіків:
- графік-поверхня;
- контурний графік;
- тривимірна гістограма;
- тривимірний графік розсіювання;
- тривимірний графік векторного поля.
Розглянемо побудову графіка-поверхні, який створюється для функції, що має два аргументи. При цьому по горизонтальних вісях відображаються значення аргументів, а вздовж вертикальної вісі – значення функції.
Для побудови графіка поверхні необхідно спочатку визначити функцію двох змінних.
Потім вибрати команду Insert | Graph | Surfare Plot або скористатися акордом клавіш <Ctrl> + <2>. У робочу область документа буде вставлена область тривимірного графіка-поверхні, яка має три перпендикулярні осі та структурний заповнювач в лівому нижньому куті.
Замість структурного заповнювача, потрібно ввести назву (без аргументів) функції. Якщо клацнути мишею за межами графіка, то створюється відповідна поверхня, рис.3.12.
Область зміни аргументів для відображення функціональної залежності в явному вигляді не задавалась. Mathcadза замовчуванням встановлює діапазон значень, для яких і будується графік. Цей діапазон можна змінити після побудови графіка. Для цього треба двічі клацнути в межах графіка і у вікні 3-D Plot Format перейти на вкладку Quick Plot Data, рис.3.13. Вкладка має три розділи. Перші два розділи називаються Range1іRange2 та містять по три поля кожний. У цих полях вказується найменше (start) і найбільше (end) значення для відображення функціональної залежності першої та другої координати. У полі # of Grids вказується число базових вузлів по координатних осях. У розділі Coordinate Systemє можливість вибрати тип координатної системи: декартова (перемикач Cartesian), сферична (Spherical) або циліндрична (Cylindrical). Змінити вигляд тривимірного графіка можна, виконавши налаштування на закладках вікна 3-D Plot Format. На рис.3.14 показано вікна на закладці General.
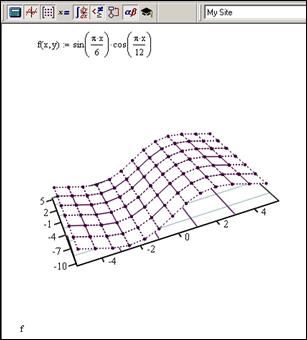
Рис.3.12. Тривимірний графік поверхні
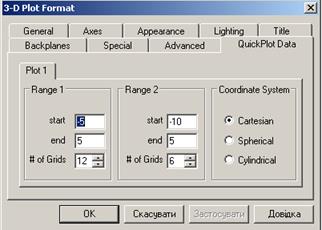
Рис.3.13. Діалогове вікно 3-D Plot відкрите на закладці Quick Plot Data
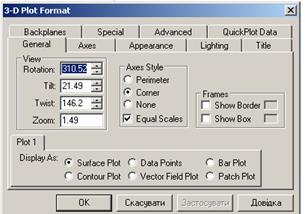
Рисунок 3.14. Діалогове вікно відкрите на закладці General
У розділі View на цій закладці є чотири поля: Rotation, Tilt, Twist вказують кути поворотів системи координат, а в полі Zoom вводиться коефіцієнт масштабування. У табл.3.1. описані способи визначення кутів орієнтації системи.
Таблиця 3.1. Кути орієнтації системи координат
| Поля для введення кута | Опис |
| Rotation | Кут повороту системи координат навколо осі Z. Значення можуть бути в діапазоні від -3600 до 3600. |
| Tilt | Кут повороту навколо осі Х системи координат, який визначається після повороту осі Z на кут, який вказаний в полі Rotation. Може приймати значення від 0 до 1800. |
| Twist | Кут повороту навколо осі Z системи координат, який оримується спочатку поворотом навколо осі Z нерухомої системи (кут вказаний в полі Rotation) і наступним поворотом навколо осі Х (вказаний в полі Tilt). Значення може бути в діапазоні від -3600 до 3600. |
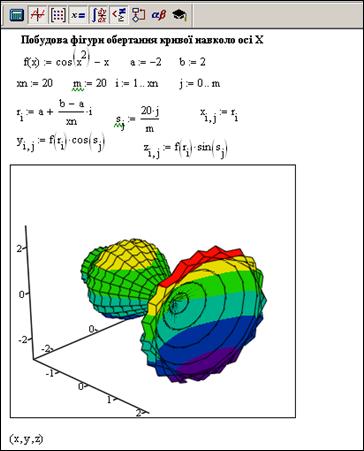
Рисунок 3.15. Фігура обертання кривої навколо осі Х
У розділі Axes Style задається спосіб відображення координатних осей. Так, перемикач Perimeter дозволяє відобразити координатні осі на передньому плані графіка, а за допомогою перемикача Cornerосі перетинаються в куті рисунка, на початку системи координат.
Розділ Frames має дві опції: Box Show BorderіShow.Опція Show Border дозволяє відобразити границі області рисунка, а опція Show Box обмежує рисунок паралелепіпедом.
Внизу вікна є група перемикачів Displey As, які дозволяють задавати тип графіка.
Для введення заголовка графіка слід скористатися закладкою Title, налаштування кольору та вибір способу заповнення областей графіка задається на закладці Apparance
Питання для самоконтролю
1. Яку послідовність дій потрібно виконати для побудови двовимірного графіка?
2. Чи можна побудувати графік функції, якщо не вказаний діапазон зміни аргумента ?
3. Як побудувати декілька графіків на одному рисунку ?
4. Як встановити маркери на осях графіка ?
5. Як здійснити підпис осей графіка та його назви ?
6. Як змінити розмір графіка ?
7. Як визначити числові значення координат точки на графіку ?
8. Як збільшити частину графіка та визначити найбільше та найменше значення координат збільшеної області ?
9. Якими символами можна відобразити базові точки графіка ?
10. Які є способи відображення двовимірних графіків ?
11. Як побудувати графік в полярних координатах ?
12. Як відформатувати графік в полярних координатах ?
13. Які є типи тривимірних графіків ?
14. Яка послідовність дій при побудові графіка-поверхні ?
15. Як змінити кут повороту системи координат тривимірного графіка ?
16. Як змінити діапазони значень на осях тривимірного графіка ?
17. Як вибрати тип координатної системи при побудові тривимірних графіків ?
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №2
Графіка в Mathcad
Мета роботи.Набути практичні навички зі створення та форматування двовимірних графіків, графіків в полярній системі координат, а також графіків функції двох змінних.
Хід роботи
1. Побудувати графік функції за даними, які наведені в табл. 2.1.
2. Скопіювати побудований графік та розмістити його копію під оригіналом.
3. На цьому рисунку додати графік функції f(х), дані для якої наведені в табл. 3.1.
4. Відформатувати обидва графіки: встановити маркери на осях, встановити сітку, графіки відобразити різними типами ліній, виконати підпис графіків і розмістити його вверху.
5. Виконати трасування для одного з графіків, та помістити значення координат певної точки в робочий документ.
6. Побудувати графік функції в полярних координатах, таблиця 3.2. Виконати форматування цього графіка: відобразити координатну сітку, встановити цифрові позначки сітки, відобразити базові точки. Завдання для побудови графіка наведені в табл. 3.2.
7. Побудувати графік функції двох змінних (3 – D Plot) типу поверхня за даними табл. 3.3.
8. Виконати форматування графіка.
9. Збільшити діапазон відображення функціональної залежності по першій та другій координаті (закладка Quick Plot Data вікна 3-D Plot Format).
10. Змінити число базових вузлів по координатних осях.
11. Добитися бажаного виду графіка, змінивши кути поворотів системи координат (поля Rotation, TiltтаTwistзакладки General).
12. Виконати підписи осей (закладки Axes) та помістити внизу підпис графіка.
Глава 4. Матриці та вектори
4.1. Матриці
У системі Mathcad закладені широкі можливості роботи з масивами, закрема з векторами та матрицями. Вектор представляє собою одновимірний масив, а матриця – двовимірний. Елементи масиву можуть мати числові чи текстові значення або самі бути масивом (вкладені масиви). Доступ до елемента масиву здійснюється через його ім’я та індекс.
Для створення масиву слід виконати команду Insert | Matrix або скористатися акордом клавіш <Ctrl>+<M>, або клацнути на логотипі матриці палітри Matrix, рис.4.1.
При цьому відкривається вікно Insert Matrix, рис.4.2, в якому потрібно вказати число рядків (поле Rows) та стовпців (поле Columns). Для створення вектора-рядка в полі Rowsтреба встановити одиницю, а для створення вектора-стовпця в полі Columns слід занести одиницю.

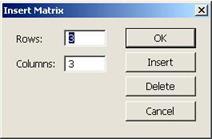
Рис.4.1. Створення Рис.4.2. Вікно Insertt Matrix
масиву з використанням
палітри Matrix
Після встановлення значень розмірності масива у вікні InsertMatrixв документі з’являється шаблон масиву. У цьому шаблоні замість структурних заповнювачів потрібно ввести значення елементів масиву. На рис. 4.3. змінній А присвоюється матриця розміром 3 х 4.
4.2. Звертання до елементів масивів
Звертання до елементу масиву здійснюється через ім’я масиву та індексу елемента.

Рис.4.3. Результат визначення масивів
Для введення індексу слід скористатися палітрою Matrix або натиснути клавішу < [>. Зокрема, цим елементам можна присвоювати нові значення і ці зміни будуть відображені в вихідному масиві. Для виведення масиву необхідно вивести ім’я масиву та знак рівності. Якщо число рядків чи стовпців не перевищує десяти, то масив відображається повністю, інакше відображається лишень його частина, і решту елементів можна переглянути, скориставшись смугами прокрутки.
Слід мати на увазі, що за замовчуванням індексація елементів починається з нуля. При звертанні до елементів одновимірних масивів також потрібно вказувати два індекси: індекс рядка та стовпця, на перетині яких розташований елемент, рис.4.4.
Для відображення вектора-стовпця спочатку ставиться індекс елемента, а потім нулевий індекс стовпця. Тут другий індекс для елемента вектора-стовпця вказувати не обов’язково тому, що за замовчування він прийнятий за нуль.
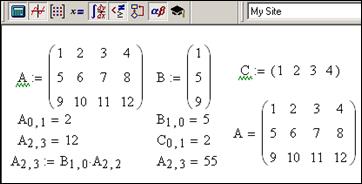
Рис.4.4. Використання змінної ORIGIN
4.3. Налаштування початкового індексу масиву
За замовчуванням початкове значення індексу рівне нулю, щоб змінити його на одиницю, необхідно перепризначити значення системної змінної ORIGIN. Це можна зробити, виконавши команду TOOLS | Worksheet Options. Перейти на закладку Built-In Variables та встановити потрібне значення в полі Array Origin (ORIGIN) (наприклад, одиницю).
Перепризначити значення ORIGIN можна також у документі оператором присвоєння, рис.4.5.
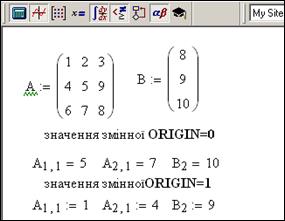
Рис.4.5. Використання змінної ORIGIN
Крім способу ініціалізації масиву з використанням шаблону із заповнювачами, елементи масиву можна обчислити за функціональною залежністю, аргументами якої є значення – діапазони індексів та стовпців, рис.4.6.
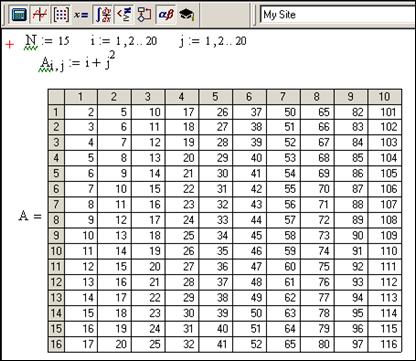
Рис.4.6. Обчислення елементів матриці
Якщо кінцеве значення діапазону зміни індексних змінних більше десяти, то в документі буде відображена частина матриці, при цьому у вікні Rezult Format на закладці Display Options зі списку Displey Style треба вибрати елемент Automatic. Індекси елемента в таблиці визначаються номерами рядків і стовпців, на перетині яких розташований цей елемент. Якщо є потреба відобразити значення масиву як матрицю будь-яких розмірів, то потрібно виконати команду Format | Rezult. На закладці Displey Options зі списку Matrix display Style вибрати елемент Matrix.
4.4. Операції з масивами
В Mathcad поряд з арифметичними операціями з масивами (рис.4.7.) можна виконувати такі операції, як транспонування, обертання, визначення матриці тощо.
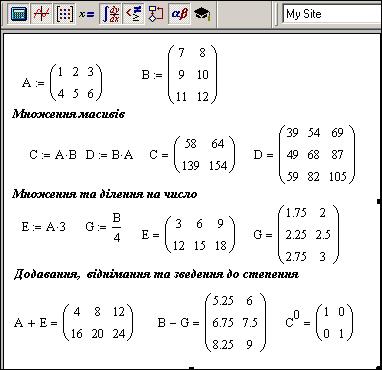
Рис.4.7. Арифметичні операції з масивами
Операція транспонування матриць полягає в тому, що рядки та стовпці міняються місцями. Транспонування матриці всікується встановленням праворуч вверху біля імені матриці літери Т. Це виконується спеціальною піктограмою (М) палітри Matrix або комбінацією клавіш <Ctrl> + <1>.
Знаходження оберненої матриці полягає в тому, що обернена матриця, будучи помножена на вихідну, в результаті дає одиничну матрицю. Це справедливо для не виродженої квадратної матриці. Ця процедура еквівалентна зведеню вихідної матриці до мінус першого степеня. На палітрі Matrix є піктограма (Х-1), що дозволяє знайти обернену матрицю, рис.4.8.

Рис.4.8. Транспонування матриці, обчислення оберненої матриці
Для визначення детермінанта матриці необхідно ім’я матриці охопити прямими дужками, що виконується комбінацією клавіш <Shift>+ <\> , або скористатися піктограмою |Х| на палітрі Matrix.
Обчислення векторного добутку матриць можна виконати з допомогою спеціального оператора, який вводиться натисненням клавіш <Ctrl> + <8> або скористатися піктограмою (  ) палітри Matrix. Для обчислення суми елементів вектора слід скористатися акордом клавіш <Ctrl> + <4>.
) палітри Matrix. Для обчислення суми елементів вектора слід скористатися акордом клавіш <Ctrl> + <4>.
Певний інтерес представляє собою процедура векторизації. Хай масив є аргументом деякої функції, яка визначена для скалярних аргументів. Застосовуючи функцію векторизації, можна обчислити значення функції для кожного елемента заданого масиву. У результаті отримати масив тих же розмірів, що і заданий, а його елементи є результатом обчислення функції для аргумента, який знаходиться в вихідному масиві на відповідному місці. Для виконання векторизації на палітрі є спеціальна піктограма ( 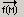 ), також можна скористатися комбінацією клавіш <Ctrl> + < – >. Перед застосуванням векторизації до певного виразу цей вираз має бути виокремлений, рис.4.9.
), також можна скористатися комбінацією клавіш <Ctrl> + < – >. Перед застосуванням векторизації до певного виразу цей вираз має бути виокремлений, рис.4.9.
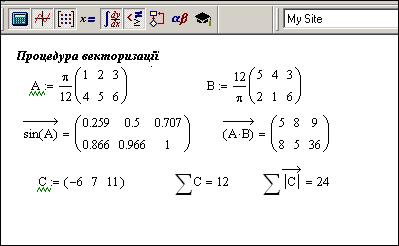
Рис.4.9. Процедура векторизації
4.5. Перетворення масивів
Інколи потрібно мати доступ не до одного елемента масиву, а до його фрагмента, зокрема до рядків чи стовпців масиву.
Для виокремлення в матриці стовпця є оператор на палітрі Мatrix (піктограма з кутовими дужками). Можна також скористатися акордом клавіш <Ctrl> + <6>. У результаті до назви матриці, з якої витягується стовпець, з’являється структурний заповнювач, де вводять верхній індекс. Це число є індексом стовпця матриці, до якого здійснюється доступ, рис.4.10.
Якщо потрібно витягнути рядок з масиву, тоді спочатку матрицю транспонують, а потім звертаються до стовпця транспонованої матриці. Результат буде вектором-стовпцем. Для того, щоб отримати вектор-рядок, одержаний вектор-стовпець треба транспонувати, рис.4.10.

Рис.4.10. Звертання до рядків та стовпців масиву
При потребі додавання рядків чи стовпців матриці, потрібно виокремити елемент матриці. Рядки будуть додаватися під рядком виокремленого елемента, а стовпці додаються праворуч від стовпця цього елемента. Після виокремлення елемента необхідно виконати команду Insert | Matrix. У діалоговому вікні Insert | Matrix в полі Rows вказати число рядків, які необхідно вставити, а полі Сolumns – стовпців та клацнути на кнопці Insert. У результаті отримаємо матрицю змінних розмірів.
Вилучення рядків та стопців виконується практично так само, лише у вікні Insert Matrix слід клацнути не на кнопці Insert, а на кнопці Delete.
Для створення матриць шляхом їх об’єднання застосовують функції stack (А,В) і argument (А,В). Функція stack (А,В) додає матрицю В знизу матриці А, очевидно, що матриця В має мати однакову кількість стовпців з матрицею А.
Функція argument (А,В) додає матрицю В праворуч матриці А, матриці А і В повинні мати однакову кількість рядків.
Функція submatrix (А, n1, n2, m1, m2) дозволяє витягнути під матрицю В з деякої матриці А. Аргументи n1, n2 це початковий і кінцевий рядки під матриці В, які витягуються з матриці А, а аргументи m1, m2 – початкові і кінцеві стовпці підматриці В.
Наприклад: В = submatrix (А, 2, 4, 1.3), тут матриця А хай має розмірність 6 х 6.
Для створення матриці, елементи якої визначаються через індекси, можна скористатися функцією matrix ( ). Функція має три аргументи: перші два – це число рядків і стовпців, потім назва функції, за якою обчислюються елементи матриці, рис.4.11.
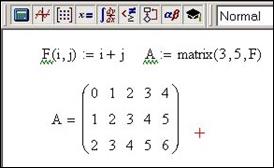
Рис.4.11. Створення матриці з допомогoю функції Matrix ( )
Тут i та j – індекси елемента матриці, за замовчуванням кількість рядків і = 0,1,2,…, М - 1, а стовпців j = 0,1,2,…, N -1.
Деякі функції призначені для визначення розмірів масивів, табл.4.1.
| Функція та її аргументи | Опис |
| Cols (A) | Повертає число стовпців матриці А. |
| Rows (A) | Повертає число рядків матриці А. |
| Last (V) | Повертає індекс останнього елемента вектора V. |
| Length (V) | Повертає число елементів вектора V. |
Питання для самоконтролю
1. Яку послідовність дій треба виконати, щоб створити матрицю?
2. Яку послідовність дій треба виконати, щоб створити вектор-стовпець та вектор-рядок ?
3. З якої цифри за замовчуванням починаються індекси елементів масивів ?
4. Як виконати налаштування початкового значення індексу масивів ?
5. Як згенерувати матрицю, елементи якої обчислюються за функціональною залежністю ?
6. Як відобразити значення масиву як матрицю будь-яких розмірів ?
7. Які арифметичні операції над масивами можна проводити? Наведіть приклад.
8. Як знайти обернену матрицю ?
9. Як виконати транспонування матриці ?
10. Як обчислити визначник матриці та векторний добуток?
11. В чому полягає суть векторизації ?
12. Як виокремити стовпець матриці ?
13. Як виокремити рядок матриці ?
14. Яка послідовність дій при додаванні рядків чи стовпців в матрицю ?
15. Яка послідовність дій при вилученні рядків чи стовпців матриці ?
16. Які функції застосовуються при об’єднанні матриць ?
17. Як створювати матрицю з допомогою функції matrix ( ) ?
18. Для чого використовується функція submatrix ( ) ?
ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ №3
Матриці та вектори
Мета роботи.Набути практичні навички зі створення масивів та виведення елементів масивів та виведення елементів масивів при різних значеннях системної змінної ORIGIN. Виконати операції з матрицями та векторами: додавання, множення, зведення до степеня, векторизації, транспонування та знаходження оберненої матриці. Створювати матриці за допомогою функції Matrix ( ), вилучення субматриці. Обчислення векторного та скалярного добутків векторів.
Хід роботи.
1. Сформувати матрицю А та вектор В. Значення елементів матриці та вектора взяти з табл.1.
2. Вивести на екран по два елементи матриці А та вектора В при значеннях системної змінної ORIGIN = 0 та ORIGIN = 1.
3. Транспонувати матрицю А та обчислити обернену матрицю і перемножити обернену матрицю на вихідну.
4. Перетворити вектор-стовпець В на вектор-рядок В1.
5. Виконати звертання до першого та другого стовпців матриці А.
6. Створити матрицю А1, долучивши до матриці А вектор-стовпець В, та матрицю А2, долучивши до матриці А вектор-рядок В1.
7. Створити матрицю А3, елементами якої є значення функції cos( ) від елементів матриці А, при цьому використати процедуру векторизації.
8. Сформувати матрицю Розміром 5 х 6, скориставшись функцією Matrix ( ). Залежність для визначення елементів матриці вибрати самостійно.
9. Вилучити з матриці D під матрицю Е розміром 2 х 3, скориставшись функцією Submatrix ( ).
10. Перемножити матрицю А на матрицю Е, обчислити визначник матриці D, звести матрицю Е до квадрату.
11. Створити вектори В2 та В3, елементами яких є другий та четвертий стовпець матриці D, та обчислити векторний та скалярний добуток цих векторів.
Глава 5. Розв’язок рівнянь та систем
5.1. Розв’язок алгебраїчних рівнянь
Розв’язок алгебраїчних рівнянь та їх систем займає значне місце в науково-технічній практиці інженера. Багато типів рівнянь і систем не мають аналітичних розв’язків. Однак такі рівняння можуть розв’язуватись чисельними ітераційними методами з заданою точністю (не більше значення системної змінної TOL).
Для розв’язку рівнянь призначена функція root( ). Якщо функція має формат root (f(x),x), то вона повертає значення x, при якому вираз чи функція f(x) набуває значення нуль, тобто отримуємо розв’язок рівняння f(x)=0. Перед звертанням до фунції root ( )треба задати наближене значення кореня рівняння.
Якщо інтервал ізоляції кореня рівняння відомий xÎ[a,b], то формат фунції такий: root ( f (x), x, a, b), причому a<b.
Початкові наближені значення коренів чи інтервал ізоляції можна знайти аналітичним чи графічним способом. Найбільш розповсюджений графічний спосіб визначення початкових наближень. Беручи до уваги те, що дійсні корені рівняння f(x)=0 – це точки перетину графіка функції f(x) з віссю абсцис, досить побудувати графік функції f(x) і визначити точки перетину f(x) з віссю OX чи відзначити на вісі OX відрізки [a,b], що містять по одному кореню.
Для пошуку комплексного кореня початкове наближення має бути комплексним числом.
Побудову графіка часто вдається спростити, замінивши рівняння f(x)=0 рівносильним рівнянням f1(x)=f2(x), тоді, побудувавши графіки функцій y1=f1(x) та y2=f2(x), шукані корені одержимо як абсциси точок перетину цих графіків (рис 5.1).
Для знаходження коренів полінома vn xn +…+v 2x2+v 1x+v 0 користуються функцією polyroots (v). Ця функція не вимагає початкового наближення та повертає всі корені (як дійсні, так і комплексні); коефіцієнти полінома знаходяться у векторі-стовпці vдовжиною n+1, рис. 5.1. Вектор v зручно створювати командою Symbol | Polinomal Coefficients.

Рис.5.1. Розв’язок рівняння
5.2. Розв’язок систем рівнянь. Розв’язок нелінійної системи рівнянь
Нелінійну систему рівнянь часто розв’язують з допомогою функції Find( ). Аргументами цієї функції вказуються змінні, відносно яких розв’язується система FIND (x1,x2, …).Число аргументів повинно бути рівним числу невідомих. Якщо у функцій вказаний лиш один аргумент, то вона повертає розв’язок одного рівняння. На рис. 5.2 наведений приклад розв’язку системи рівнянь з використанням функції Find( ).
Спочатку задають початкові наближення для всіх невідомих, тому що Mathcad використовує ітераційні методи розв’язку системи рівнянь. Далі вводять ключове слово Given, а за цим словом слідують рівняння та нерівності в будь-якій послідовності ( на рис. 5.2 – два рівняння). Між правою та лівою частиною рівнянь стоїть символ  (логічне дорівнює). Цей символ можна ввести, скориставшись палеткою Boolean або акордом клавіш <Ctrl>+<=>.
(логічне дорівнює). Цей символ можна ввести, скориставшись палеткою Boolean або акордом клавіш <Ctrl>+<=>.
Потім як задана система рівнянь, викликається функція Find( ), а її аргументами будуть змінні, стосовно яких система рзв’язується. Всередині блоку розв’язку рівнянь не допускаються вирази: обмеження знаком 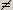 ; дискретний аргумент або вирази, що містять дискретний аргумент; нерівність виду a<b<c.
; дискретний аргумент або вирази, що містять дискретний аргумент; нерівність виду a<b<c.
Функція Find( ) може бути використана, як і будь-яка інша функція, зокрема:
1) a:=Find(x) – результат скаляр;
2) var:=Find(var1,var2…) – результат вектор.
Це зручно тоді, коли результати розв’язку рівнянь потрібно використати в іншому місці робочого документа.
3) f(a,b,c,…):=Find(x,y,z,…). Ця конструкція зручна для багаторазового розв’язку рівнянь при різних значеннях деяких параметрів А,В,С,…, які безпосередньо входять у систему рівнянь.
Для розв’язування системи нелінійних рівнянь використовується також функція Minerr( ). Ця функція аналогічна функції Find( ). Аргументи цієї функції вказують змінні, відносно яких розв’язується система Minerr(x1,x2,…). Ця функція також використовує ітераційний алгоритм розв’язку. Різниця між функцією Given( ) полягає в тому, що, якщо в результаті пошуку розв’язку не може бути отримане наступне уточнене наближення, то функція Minerr( )повертає відповідь, яка мінімізує відповідний функціонал нев’язки. Однак функція Minerr( ) не може перевірити, чи реалізує відповідь абсолютний мінімум для функціонала нев’язки. Тому при використанні цієї функції потрібно завжди включати додаткову перевірку достовірності отриманих результатів, рис.5.3.
Приклад. Розв’язати систему нелінійних рівнянь:
sin(x+2) – 3 y  = 1.2
= 1.2
2 x – sin(y – 0.5) = 1
Для розв’язку цієї системи побудуємо графіки залежності y(x) та f(y).Для цього проведемо елементарні перетворення рівнянь, записавши невідомі змінні як функції:
f2(x):=(sin(x+2)-1.2)/3 та f1(y):=(1+sin(y-0.5))/2.
Побудувавши графіки отриманих функціональних залежностей, знаходимо наближено координати точки перетину функцій, які і будуть початковим наближенням коренів системи рівнянь. Далі уточнюємо значення коренів системи рівнянь, скориставшись функцією minerr( ), рис.5.3.
Система лінійних алгебраїчних рівнянь записується в матричному вигляді як AX=B,тут А – квадратна матриця коефіцієнтів системи, а Х та В – вектори невідомих змінних і правих частин рівнянь відповідно.
Тоді розв’язок системи, яким є вектор невідомих Х, можна визначити як добуток матриці, оберненої до матриці коефіцієнтів на вектор правих частин, тобто X=A-1B.
Систему лінійних рівнянь зручно розв’язувати також з допомогою функції lsolve( )в виглядіX=lsolve(A,B).
На рис 5.4. наведений приклад розв’язку системи лінійних алгебраїчних рівнянь третього порядку з використанням оберненої матриці та функції lsolve( ).
При розв’язуванні системи лінійних рівнянь не рекомендується використовувати функцію FIND( ), тому що значення коренів системи залежить від початкового
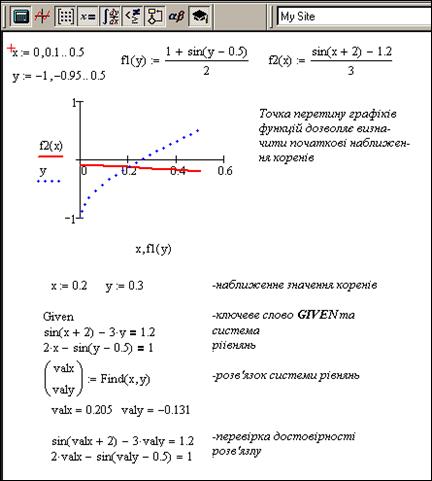
Рис.5.2. Розвязок неінійної системи рівнянь,функція Find
наближення, рис.5.5. На рис.5.6. для тієї ж системи знайдено ще один розв’язок.

Рис.5.3. Розв'язок системи нелінійних рівнянь,функція Minerr()

Рис.5.4. Розв'язок системи лінійних рівнянь

Рис.5.5. Розв'язок системи лінійних рівня

Рис.5.6. Розв'язок системи лінійних рівня
Питання для самоконтролю
1. Назвіть способи знаходження початкових наближень.
2. Які функції для розв’язку одного рівняння є в Mathcad’i ?
3. Які аргументи функції root не обов’язкові ?
4. В яких випадках Mathcad не може знайти корінь рівняння?
5. Як системна змінна TOL впливає на розв’язок рівняння з допомогою функції root?
6. Назвіть функції розв’язку системи рівнянь у Mathcad’i та особливості їх застосування.
7. Опишіть структуру блоку розв’язування рівнянь.
8. Який знак рівності використовується в блоці розв'язування і як його вставити в документ з допомогою миші та клавіатури ?
9. Які вирази не припустимі в середині блоку розв’язування рівнянь?
10. Опишіть способи використання функції Find( ).
11. Дайте порівняльну характеристику функціям Find( ) та Minerr( ).
12. Як розв’язувати систему рівнянь, які представлені у вигляді матриць?
ЗАВДАННЯ ДО ПРАКТИЧНОЇ РОБОТИ №4
Розв’язування рівнянь та систем лінійних і нелінійних алгебраїчних рівнянь.
Мета роботи. Засвоїти послідовність дій при розв’язуванні алгебраїчних рівнянь та їх систем засобами Mathcad’у із застосуванням функцій root( ), Find( ), Minerr(), lsolve( ).
Хід роботи:
1.Побудувати графік функції f(x)з метою визначення інтервалу ізоляції кореня. Вираз дляf(x)наведений в табл.5.1.
2.Розв’язати рівняння f(x)=0 з точністю е=0.0001 з використанням функції root( )таFind( ).
3. Виконати перевірку точності знаходження кореня.
4. Для системи нелінійних рівнянь (таблиця 5.2) побудувати графік залежності y(x)таx(y)з метоюзнаходження наближених значень коренів xтаy,рис.5.3. Розв’язати систему рівнянь з допомогою функцій find( )таminerr( ).
5. Виконати перевірку точності знайдених коренів.
6. За даними таблиці 5.3 розв’язати систему лінійних алгебраїчних рівнянь третього порядку з допомогою функції lsolve( ) та оберненої матриці, рис.5.4.
Таблиця 5.1. Варіанти завдань. Лінійні рівняння.
| № варіанту | Рівняння | Точність розв’язку |

| 0,0001 | |
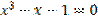
| 0,001 | |
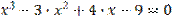
| 0,001 | |

| 0,001 | |

| 0,0001 | |
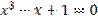
| 0,001 | |
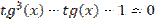
| 0,001 | |
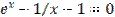
| 0,0001 | |

| 0,001 | |
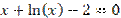
| 0,0001 | |
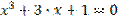
| 0,0001 | |
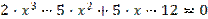
| 0,001 | |
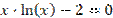
| 0,001 | |
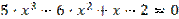
| 0,001 | |
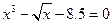
| 0,0001 | |
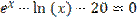
| 0,0001 | |
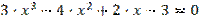
| 0,0001 | |

| 0,001 | |
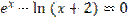
| 0,001 | |
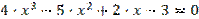
| 0,001 |
Таблиця 5.2. Варіанти завдань. Система нелінійних рівнянь.
| № 1 | sinx+2y=2; cos(y-1)+x = 0.7. | № 2 | tg(xy+0.1)=x2; x2 +2y 2 =1. |
| № 3 | cosx+y=1.5; 2x-sin(y-0.5)=1. | № 4 | sin(x+y)-1.2x=0.2; x2 +y2=1. |
| № 5 | sin(x+0.5)-Y=1; cos(y-2)+x=0. | № 6 | tg(xy+0.3)=x2; 0.9x2 +2y2=1. |
| № 7 | cos(x+0.5)+y=0.8; siny-2x=1.6. | № 8 | sin(x+y)-1.3x=0; x2 +y2=1. |
| № 9 | sin(x-1)-y=1.3-y; x-sin(y+1)=0.8. | №10 | tgxy=x2; 0.8x2 +2y2=1. |
| №11 | 2y-cos(x+1)=0; x+siny=-0.4. | №12 | sin(x+y)-1.5x=0.1; x2+y2=1. |
| №13 |
Генерация страницы за: 0.234 сек.
