Закон соответственных состояний.
Если поверхности состояний разных газов геометрически подобны, то при соответствующем масштабном преобразовании они должны совпадать. Термодинамическая поверхность, которая представляет собой ряд совмещенных поверхностей состояний нескольких газов, должна описываться уравнением, не содержащим индивидуальных коэффициентов. Впервые на возможность получения такого уравнения указал Ван-дер-Ваальс. Подставив в уравнение Ван-дер-Ваальса выражения для a, b и R, включающие критические параметры, получим
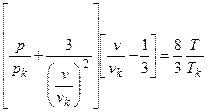 .
.
Используя приведенные параметры (р/рk=π – давление, v/vk=φ – объем, T/Tk=τ – температура), получим уравнение
(π+3/φ2)(3φ–1)=8τ,
известное как приведенное уравнение Ван-дер-Ваальса.
Таким образом, все вещества подчиняются одному уравнению состояния, если оно выражено через приведенные переменные. Это весьма важный закон термодинамического подобия – закон соответственных состояний. Два или несколько различных веществ с двумя равными одноименными приведенными параметрами находятся в соответственных состояниях. При этом, несмотря на присущие телам различия, их термодинамические поверхности совпадают; в результате и свойства тел (определяемые характером поверхности) в этих состояниях одинаковые. Закон соответственных состояний имеет большое прикладное значение как основа обобщения теоретических и экспериментальных данных для реальных веществ. В действительности приведенные термодинамические поверхности различных реальных веществ полностью не совпадают, и подобие является приближенным. Одним из дополнительных условий, при котором подобие выполняется более строго, является условие равенства коэффициентов сжимаемости zk в критической точке.
10. Процесс i=const. Дросселирование.
Адиабатное расширение газа в открытой системе в условиях стационарного течения без совершения внешней работы и приращения скорости на контрольной поверхности называется дросселированием. Стационарность течения предполагает в первую очередь постоянство давлений до и после дросселирования, а условие отсутствия приращения скорости течения на контрольной поверхности не исключает возможности ее местного увеличения (или уменьшения) внутри системы, например в самом дроссельном устройстве.
Для практического осуществления этого процесса на пути газа устанавливают какое-либо гидравлическое сопротивление: дроссельный вентиль, заслонку, калиброванное отверстие и пр.
Применив уравнение сохранения энергии для модели стационарной или находящейся в установившемся состоянии открытой системы для процесса дросселирования при l=0 и q=0 получим
i2=i1=const или u1+p1v1=u2+p2v2=const.
Никаких предположений о свойствах газов не делали, поэтому полученный результат справедлив как для идеального, так и для реального газа: при дросселировании энтальпия газа не изменяется.
При дросселировании идеального газа
di=0 (i=const) → dT=0 (T=const); du=0 (u=const).
Для реального газа при дросселировании
di=0 (i=const); dT≠0; du≠0.
Таким образом, температура реального газа при дросселировании может снижаться и повышаться.
Процесс дросселирования необратим. Для идеального газа он необратим полностью, так как не сопровождается эффектами, которые могли бы способствовать возвращению в исходное состояние. Процесс дросселирования реального газа частично обратим, так как сопровождается изменением температуры; при этом создается «тепловой резервуар» с температурой более высокой или более низкой и существует возможность использования перепада температур для получения работы (эту работу можно использовать для возвращения газа в исходное состояние).
Изменение температуры реального газа при дросселировании
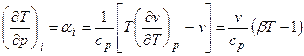 .
.
Величина 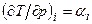 – дифференциальный эффект Джоуля–Томсона, определяющий изменение температуры при бесконечно малом падении давления в процессе дросселирования; β – температурный коэффициент объемного расширения.
– дифференциальный эффект Джоуля–Томсона, определяющий изменение температуры при бесконечно малом падении давления в процессе дросселирования; β – температурный коэффициент объемного расширения.
Уравнение справедливо как для газов, так и для жидкостей.
Практически при дросселировании всегда имеется конечная разность давлений, поэтому для такого процесса
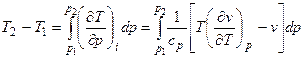 .
.
Это выражение определяет так называемый интегральный эффект Джоуля–Томсона (изменение температуры при конечной разности давлений).
11. Процесс u=const.
Если процесс расширения газа осуществить при тех же условиях, что и процесс дросселирования, т.е. без теплообмена с окружающими телами и без совершения внешней работы, но в отличие от дросселирования расширять газ в закрытой системе, т.е. не в условиях стационарного течения, а в устройстве с жесткими стенками, то полная внутренняя энергия газа в такой системе будет постоянна. Это процесс расширения u=const; какого-либо характерного названия он не имеет.
Изменение температуры газа в процессе u=const можно определить из уравнений:
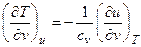
или
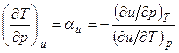 .
.
Т.к.
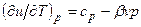 ;
;
тогда
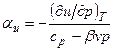 .
.
Для идеального газа 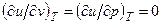 , поэтому и dТ=0 в процессе u=const.
, поэтому и dТ=0 в процессе u=const.
В процессе u=const для любого реального газа αu – всегда положительная величина, т.е. температура снижается. Интегральный эффект изменения температуры в процессе u=const
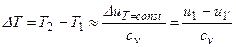 .
.
Дата добавления: 2015-05-16; просмотров: 1710;
