Условие конечности очереди при обслуживании входных потоков в системах массового обслуживания.

Это условие, означающее также, что СМО справляется с обслуживанием потока, имеет вид неравенства:

l < n m , (1)

где l -интенсивность входного потока заявок, n – число обслуживающих аппаратов, m - интенсивность обслуживания.

Здесь произведение nm характеризует суммарную производительность обслуживающих аппаратов - среднее количество заявок, которое могут обслужить все n обслуживающих аппаратов. Условие (1) означает, что суммарная производительность ОА должна быть выше среднего числа заявок, поступающих в единицу времени на обслуживание.

Выражение (1) называется также условием конечности очереди. Если это условие не выполняется, в СМО наблюдается неограниченный рост очереди.

Пример. Агентство по продаже авиабилетов располагает n=2 кассами. Среднее время продажи билетов одним кассиром равно γ = 3 мин, интенсивность входного потока равна l=3 пас/мин.

1. Справляется ли агентство с обслуживанием пассажиропотока?

2. Какое число касс минимально необходимо, чтобы агентство справлялось с обслуживанием?

Решение. Интенсивность обслуживания равна:

m = 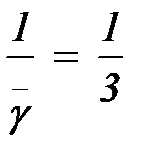пас/мин

Условие того, что система массового обслуживания справляется с обслуживанием, имеет вид неравенства (2.14). Поскольку правая часть неравенства равна 2/3, то, очевидно, что неравенство не выполняется. Таким образом, агентство при n=2 работающих касс не справляется с обслуживанием пассажиропотока заданной интенсивности.

Минимально необходимое число касс должно удовлетворять неравенству:

n >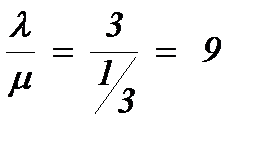

Следовательно, минимально необходимо n=10 касс