Дискретное преобразование Фурье
При машинной обработке вместо интеграла Фурье приходится пользоваться его приближением, подсчитанным с помощью конечной суммы. В результате возникают дополнительные эффекты, а теория дискретного преобразования Фурье становится самостоятельной дисциплиной.
Рассмотрим 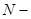 мерное пространство последовательностей длины
мерное пространство последовательностей длины 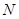 . Каждый элемент этого пространства имеет вид
. Каждый элемент этого пространства имеет вид 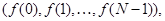 где
где 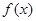 - некоторая функция, принимающая комплексные значения. В этом пространстве рассмотрим набор векторов, составленный из последовательностей
- некоторая функция, принимающая комплексные значения. В этом пространстве рассмотрим набор векторов, составленный из последовательностей 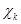 , построенных по функциям
, построенных по функциям 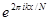 ,
, 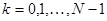 . В пространстве определено скалярное произведение:
. В пространстве определено скалярное произведение:
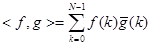 . Имеет место равенство
. Имеет место равенство 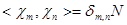 . Это означает, что последовательности
. Это означает, что последовательности 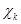 составляют базис пространства. При этом для произвольной функции
составляют базис пространства. При этом для произвольной функции 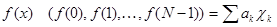 , где
, где 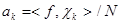 . Эти две формулы обычно записывают в виде
. Эти две формулы обычно записывают в виде
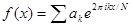 ,
, 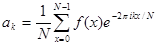 (1)
(1)
и называют дискретным преобразованием Фурье. Из последней формулы следует, что 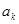 есть аналог значения преобразования Фурье исходной функции, вычисленного в точке
есть аналог значения преобразования Фурье исходной функции, вычисленного в точке 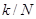 .
.
Дата добавления: 2015-05-13; просмотров: 1071;
