Полосовой фильтр на основе фильтра низких частот
В предыдущей лекции было показано, каким образом можно построить различные фильтры. Оказывается, любой из таких фильтров можно получить на основе фильтра низких частот с помощью универсальной процедуры.
|
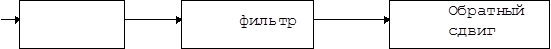
Пусть имеется сигнал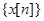 
с преобразованием Фурье 
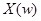. Рассмотрим новую последовательность 
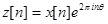. По определению 
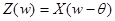. Если нам нужен полосовой фильтр, можем поступить следующим образом. Сдвиг осуществляется генератором на основе осциллятора, о котором будет сказано ниже. Обратный сдвиг осуществляется так же.
Непосредственное применение указанного способа не удобно, поскольку приходится работать с комплексными числами, и в результате обратного сдвига получается, как правило, комплексный сигнал. Выход заключается в преобразовании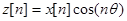 
. В результате 
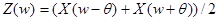. Если исходный сигнал имеет ограниченный спектр и 
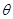выбран так, что носители 
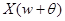и 
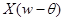не пресекаются, задача решается без применения комплексных чисел. Например, пусть спектр 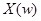находится в интервале 2kHz-4kHz, и требуется получить лишь часть сигнала в диапазоне 2.5kHz-3.5kHz. Выбираем 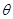=3kHz и используем фильтр низких частот с полосой пропускания 0.5kHz. После обратного сдвига придется использовать еще один фильтр низких частот с полосой пропускания 3.5kHz.
Дата добавления: 2015-05-13; просмотров: 727;