Полосовой фильтр

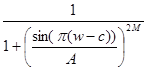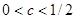Рассмотри выражение , где . Очевидно, что эта функция достигает своего максимума при 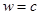. Это означает, что передаточная функция изображает полосовой фильтр. При замене в выражении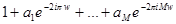 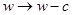получим фильтр с комплексными коэффициентами. Формально - это решение задачи, однако использование комплексного фильтра для фильтрации вещественного сигнала не очень удобно. Поэтому используют выражение вида 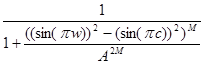. Для четного 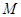. Оно снова достигает максимума при 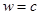. Используя ту же технику, что и в предыдущем случае, после замены 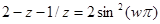снова сведем задачу к отысканию корней квадратного уравнения.