Измерения апикального базиса
Апикальный базис - это условная линия, проходящая на уровне верхушек корней зубов на верхней и нижней челюстях. В преддверии полости рта она проецируется на переходную складку. Размеры апикального базиса изучают в трансверсальном (ширина) и сагиттальном (длина) направлениях по методу Хауса (Haus) в модификации Н.Г. Снагиной.
Ширина апикального базиса верхней челюсти определяется на гипсовой модели по прямой между наиболее глубокими точками в области fossae canina (в углублении между верхушками клыков и первых премоляров), а на модели нижней челюсти измерение проводится между этими же зубами, отступя от уровня десневого края на 8 мм (рис.7.37, 7.38). Длина апикального базиса измеряется на верхней челюсти от
Таблица 7.17 Ширина зубных рядов, ширина и длина апикального базиса челюстей в зависимости от суммы мезиодистальных размеров 12 зубов (по Н.Г. Снагиной).
| Сумма размеров 12 зубов | Ширина зубного ряда | Ширина | Длина | Ширина | Длина | |
| В области 4|4 | В области 6|6 | апикального базиса верхнего зубного ряда | апикального базиса нижнего зубного ряда | |||
| 29.4 | 37.8 | 33.0 | 29.2 | 30.0 | 32.2 | |
| 29.7 | 38.3 | 33.4 | 29.6 | 30.4 | 32.6 | |
| 30.1 | 38.8 | 33.8 | 30.0 | 30.8 | 33.1 | |
| 30.5 | 39.2 | 34.3 | 30.4 | 31 2 | 33.5 | |
| 30.9 | 39.8 | 34.7 | 30.8 | 31.6 | 33.9 | |
| 31.3 | 40.3 | 35.2 | 31.2 | 32.0 | 34.4 | |
| 31.7 | 40.8 | 35.6 | 31.5 | 32.4 | 34.8 | |
| 32.1 | 41.3 | 36.0 | 31.9 | 32.8 | 35.2 | |
| 32.5 | 41.8 | 36.5 | 32.3 | 33.2 | 35.6 | |
| 32.9 | 42.3 | 36.9 | 32.7 | 33.6 | 36.1 | |
| 33.3 | 42.8 | 37.4 | 33.1 | 34.0 | 36.5 | |
| 33.7 | 43.3 | 37.8 | 33.5 | 34.4 | 36.9 | |
| 34.1 | 43.8 | 38.2 | 33.9 | 34.8 | 37.4 | |
| 34.4 | 44.3 | 38.7 | 34.3 | 35.2 | 37.8 | |
| 34.8 | 44.8 | 39.1 | 34.7 | 35.6 | 38.2 | |
| 35.2 | 45.3 | 39.6 | 35.1 | 36.0 | 38.7 | |
| 35.6 | 45.8 | 40.0 | 35.4 | 36.4 | 39.1 | |
| 36.0 | 46.3 | 40.4 | 35.8 | 36.8 | 39.5 | |
| 36.4 | 46.8 | 40.9 | 36.9 | 37.2 | 39.9 | |
| 36.8 | 47.3 | 41.3 | 36.6 | 37.6 | 40.6 | |
| 37.2 | 47.8 | 41.8 | 37.0 | 38.0 | 40.8 | |
| 37.6 | 48.3 | 42.2 | 37.4 | 38.4 | 41.2 | |
| 39.0 | 48.8 | 42.6 | 37.8 | 38.8 | 41.7 | |
| 38.5 | 49.3 | 43.1 | 38.2 | 39.2 | 42.1 | |
| 38.8 | 49.8 | 43.5 | 38.6 | 39.6 | 42.5 | |
| 39.2 | 50.4 | 44.0 | 39.0 | 40.0 | 43.0 | |
| 39.5 | 50.9 | 44.4 | 39.3 | 40.4 | 43.4 | |
| 39.9 | 51.4 | 44.8 | 39.7 | 40.8 | 43.8 | |
| 40.3 | 51.9 | 45.3 | 40 1 | 41.2 | 44.2 | |
| 40.7 | 52.4 | 45.7 | 40.5 | 41.6 | 44.7 | |
| 41 1 | 52.9 | 36.2 | 40.9 | 42.0 | 45.1 | |
| 41.5 | 53.4 | 46.6 | 41.3 | 42.4 | 45.5 | |
| 41.9 | 53.9 | 47.0 | 41.7 | 42.8 | 46.0 |
точки А (место пересечения срединного небного шва с линией, соединяющей центральные резцы в области шейки с небной поверхности) по срединному небному шву до линии, соединяющей дистальные поверхности первых постоянных маляров. На нижней челюсти - от точки Б (передняя поверхность режущих краев центральных резцов) по перпендикуляру до пересечения с линией, соединяющей дистальные поверхности первых постоянных моляров. Зависимость длины и ширины апикального базиса от суммы мезиодистальных размеров 12-ти постоянных зубов представлена в табл. 7.17.
В норме ширина апикального базиса верхней челюсти составляет 44%, нижней - 40% от суммы мезиодистальных размеров 12-ти постоянных зубов каждой челюсти. С этим же параметром связана ширина зубных рядов в области премоляров (39.2%) и моляров (50.4%). Так, например, если сумма мезиодистальных размеров 12-ти зубов составляет 100 мм, то ширина апикального базиса верхней челюсти составляет 44 мм, нижней - 40 мм, а ширина зубного ряда в области премоляров равна 39.2 мм и в области моляров - 50.4 мм.
1.2. Графические методы диагностики Изучение формы зубных рядов
Форма верхнего и нижнего зубных рядов в период прикуса молочных зубов — полукруг, в период прикуса постоянных зубов верхняя зубная дуга имеет форму полуэллипса, нижняя — параболы (рис. 7.39, 7.40).
Оценивать форму зубных рядов можно с помощью графических методов, используя различные приспособления или геометрические построения (симметроскопия, фотосимметроскопия, симметрография, параллелография, диаграмма Хаулея-Гербера-Гербста).
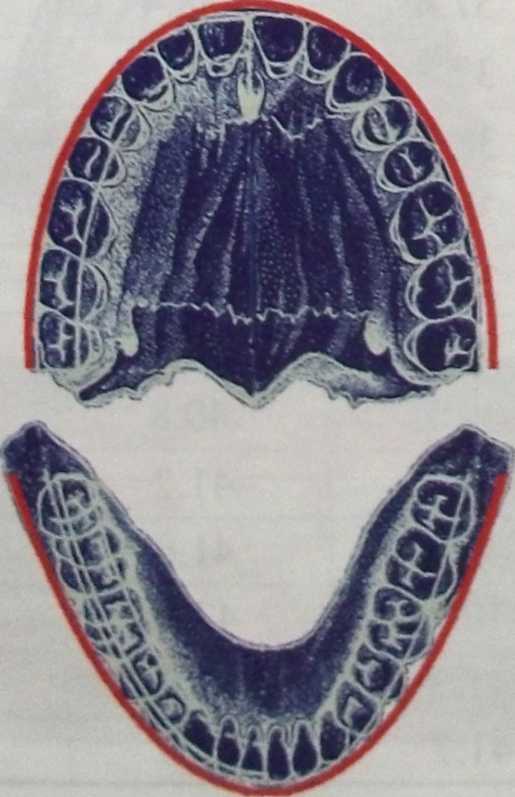
| Рис. 7.39. Нормальная форма верхнего и нижнего зубного ряда |
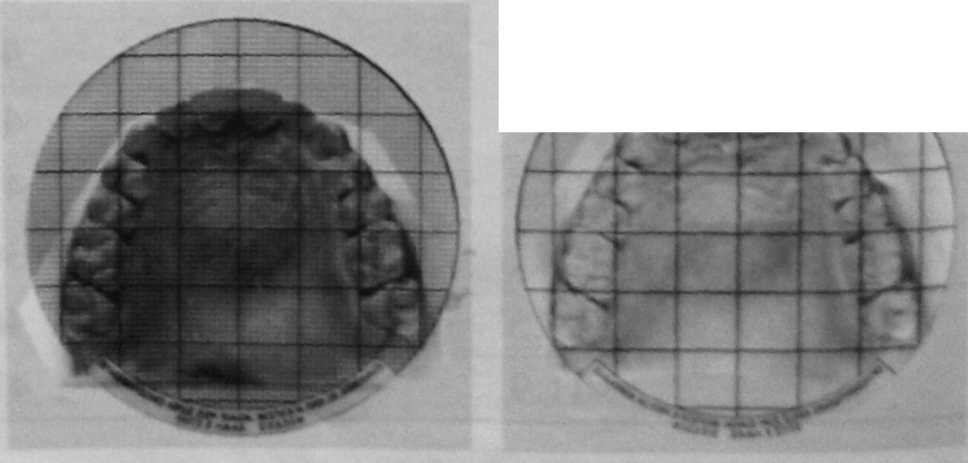
| Рис. 7.41.Симметроскопия верхнего зубного ряда |
Симметроскопия. С помощью этого метода изучают место расположения зубов трансверсальном и сагиттальном направлениях. Ортокрест (ортодонтический крест) применяют для экспресс-диагностики. Он представляет собой прозрачную пластику; на которой нанесен крест с миллиметровыми делениями или миллиметровая сетка с делениями через 1 -2 мм. Пластину накладывают на гипсовую модель верхней челюсти, ориентируют крест по срединному небному шву, и затем изучают расположение зубов по юс отношению к срединной и поперечной линиям (рис. 7.41).
Фотосимметроскопия представляет собой метод симметроскопии диагностических моделей челюстей с последующим их фотографированием в определенном режиме.
Фотографию моделей челюстей со спроецированной на нее миллиметровой сеткой в дальнейшем изучают и измеряют.
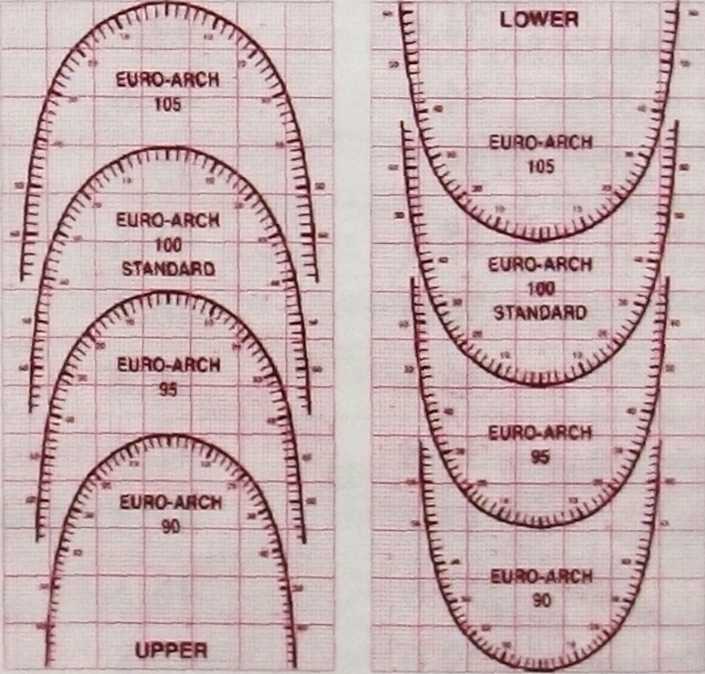
| Рис. 7.40. Формы зубных рядов в зависимости от размеров зубов |
Симметрография. Авторами симметрографов различных конструкций являются Ван Лук, Симон, Коркхауз, Филипс, Брух, Пазма, ВН. Володкин. В этих приборах изучаемую диагностическую модель челюсти ориентируют, а затем фиксируют относительно перпендикулярно расположенных измерительных шкал. Для удобства и точности исследования основание, на котором фиксируют модель челюсти, вращают. Оно имеет градуировку, что позволяет повернуть модель челюсти под нужным
углом к измерительным шкалам. Затем визиром симметрографа наносят на модель челюсти разметку, изучают симметричность расположения зубов и форму зубного ряда.
Если визир гнатографа Симона, симметрографа Коркхауза или другого подобного измерительного аппарата соединен с передающей системой, то можно воспроизвести на плоскости (чаще на миллиметровой бумаге) контуры зубного ряда натурального или увеличенного размера, проекцию зубных рядов друг на друга, кривые небного свода в различных сечениях.
Параллелография. Данный метод целесообразно использовать при применении измерительного устройства, которое предложил М.З. Миргазизов с соавторами. Это усовершенствованный параллелометр с угломерным механизмом, который позволяет проводить сагиттальные, трансверсальные и угловые измерения. На модели челюсти находят условную базовую точку отсчета. В качестве такой точки авторы используют точку пересечения сагиттальной и трансверсальной плоскостей с мезиальной поверхностью первых постоянных моляров.

| Рис. 7.43. Сопоставление трафаретов форм зубных рядов с суммой мезиодистальных размеров резцов и клыке (18 и 26 мм). |
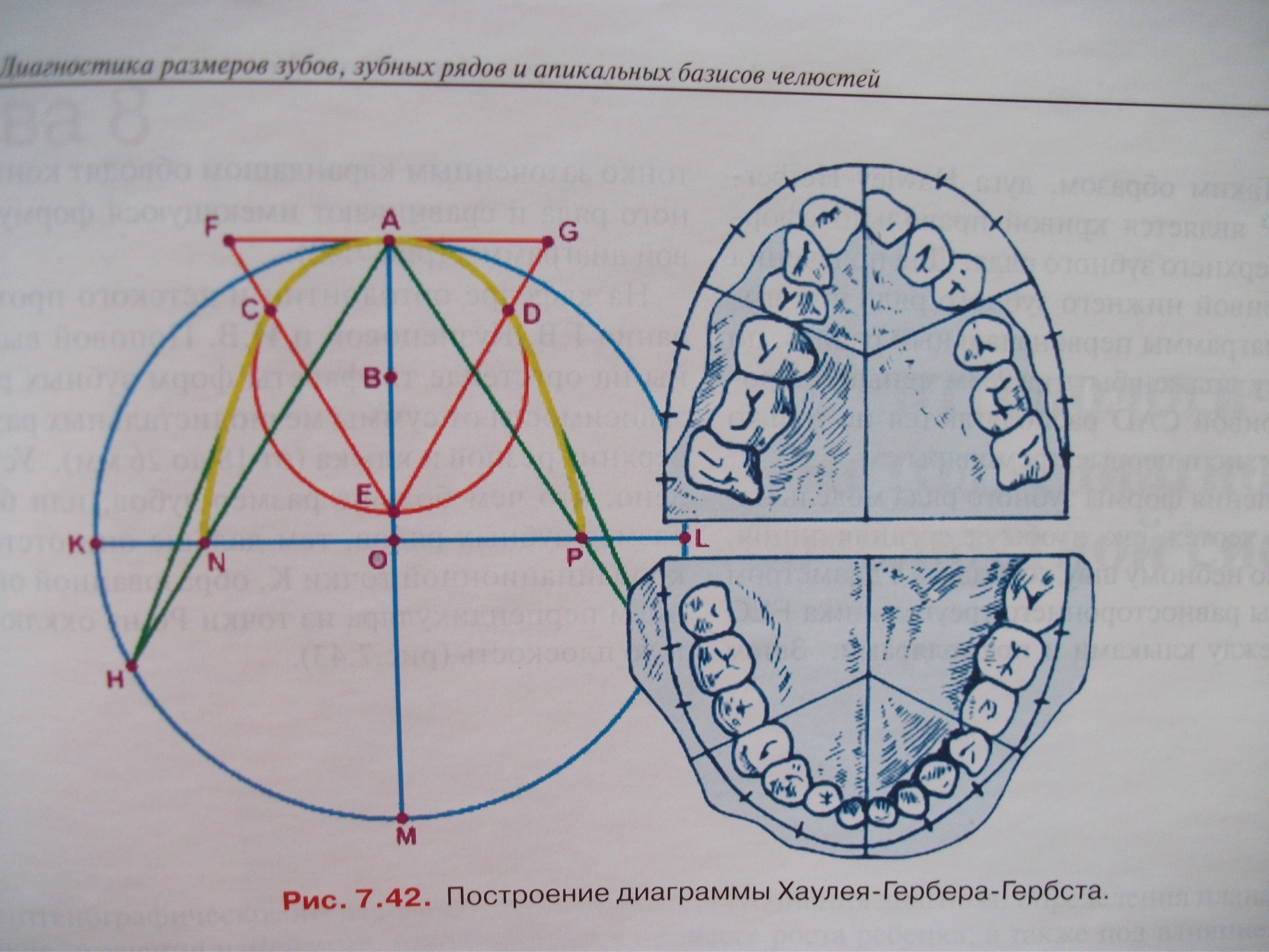
На дополнительном круге из точки М диаметром AM откладывают радиусом АО точки J и Н. Соединив точку Н с точкой С и точку J с точкой D, получают кривую HCADJ, которая является кривой всей верхней зубной дуги по Hawley. На отрезках НС и DJ должны располагаться боковые зубы. Herbst заменил боковые прямые линии дугами CN и DP. Центрами этих дуг являются точки L и К, лежащие на диаметре (KL), перпендикулярном диаметру AM. Дугу у CN описывают радиусом LC и дугу DP - радиусом KD. Таким образом, дуга Hauley-Herber-Herbst NCADP является кривой правильно сформированного верхнего зубного ряда. Для получения правильной кривой нижнего зубного ряда при вычерчивают диаграммы первоначальный радиус, по мнению Hawley должен быть на 2 мм меньше. Кроме того, на кривой CAD располагаются не только резцы и клыки, но и первые премоляры.
Для определения формы зубного ряда модель накладывают на чертеж так, чтобы ее средняя линия, прокатам по небному шву, совпадала с диаметром АМ, а стороны равностороннего треугольника FEG проходили между клыками и премолярами. Затем тонко заточенным карандашом обводят контур зубного ряда и сравнивают имеющуюся форму с кривой диаграммы (рис.7.42).
На кафедре ортодонтам и детского протезирования Г.В. Кузнецовой и И.В Поповой выполнены на оргстекле трафареты форм зубных рядов в зависимости от суммы мезиодистальных размеров верхних резцов и клыка (от 18 до 26 мм). Установлено, что чем больше размер зубов, или больше размер зубных рядов, тем дальше они отстоят от координационной точки 1С, образованной опусканием перпендикуляра из точки Ро на окклюзионную плоскость (рис.7.43).
Дата добавления: 2015-05-13; просмотров: 6970;
