Б. Многократные измерения

В случае однократного измерения нельзя сказать ничего определенного ни о случайной погрешности, ни о степени приближения измеряемой величины 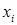к истинному значению искомой величины .

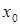Допустим, что мы выполнили серию в 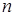измерений 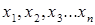искомой величины и уже исключили систематические погрешности. Тогда (при большом числе наблюдений, в силу случайного характера 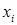) 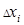будут встречаться одинаково часто как со знаком (-), так и со знаком ( 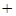) (см. с.4, п.7).

Поэтому при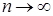

,

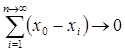откуда следует, что в пределе

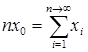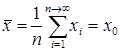и . (4)

Таким образом, при 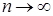среднеарифметическое из всех 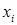будет стремиться к истинному значению искомой величины 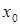, которое позволит найти случайные погрешности. В итоге многократные наблюдения открывают путь нахождения величины, близкой к 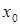, и доверительных границ. Однако задача осложняется тем, что реализовать бесконечное число наблюдений невозможно. Поэтому для ее решения привлекают аппарат математической статистики.