Определение кинетических констант горения

Расчет процессов горения требует знания кинетических констант горения Е и k₀, которые определяются экспериментально (расчетом - только для простейших химических реакций). Прямое определение констант горения по измерениям концентраций или по толщине фронта пламени неприемлемо, поскольку толщина фронта пламени составляет доли миллиметра.

Наиболее просто определяется нормальная скорость распространения пламени с помощью горелки Бунзена (рис. 3.8).

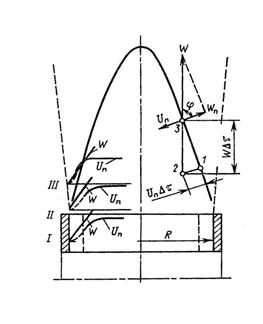
Рисунок 3.8 - Горелка Бунзена

Представим себе горелку в виде вертикальной трубки, в которую подается газовоздушная смесь с недастатком окислителя при a<1. Смесь сгорает, образуя конусообразный факел. Часть недогоревшего газа догорит с воздухом из атмосферы. Для устойчивого горения факела необходимо, чтобы в каждой точке фронта горения нормальная к ней составляющая скорости движения газа W (Wcosj) равнялась нормальной скорости распространения пламени U_n

U_n=Wcosj.

Зная распределение скорости по радиусу W=f(r) и угол j, можно определить U_n и это сложно, так как поле скоростей по радиусу и значение угла j переменно. Принимая во внимание, что внутренний фронт имеет форму конуса, и учитывая, что количество подаваемой газовоздушной смеси G = 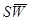должно равняться количеству смеси, сгорающей во фронте пламени 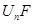, получим соотношение

,

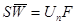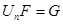, (3.11)

где S – площадь сечения горелки;

F – площадь конуса фронта пламени;

- средняя по расходу скорость;

G – расход исходной газовоздушной смеси.

Выражая скорость нормального распространения пламени как

и подставляя выражение для площади боковой поверхности конуса

,

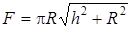где h – высота конуса пламени,

R – радиус горелки,

в окончательном виде получим выражение для расчета скорости нормального распространения пламени через размеры конуса пламени:

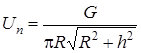. (3.12)

3.5 Условия устойчивой работы кинетических горелок

В предварительно подготовленной однородной смеси интенсивность горения зависит только от кинетики химических реакций, поэтому такой вид горения называется кинетическим горением. В зависимости от режима движения горящей смеси различают ламинарное и турбулентное кинетическое горение.

При ламинарном движении смеси скорость ее движения распределяется в горелке по параболе, аналогичное распределение скоростей сохраняется и на выходе из горелки. Условием устойчивости ламинарного горения является равенство скоростей движения и горения смеси

W = – U_n

на периферии основания факела (рис. 3.8).

Для однородной газовой смеси заданного состава нормальная скорость распространения пламени U_n - величина постоянная. На периферии U_n уменьшается: внутри горелки за счет охлаждающего действия стен, а на выходе из горелки (при a < 1) за счет разбавления горючей смеси воздухом. Вблизи границ струи горение прекращается т.к. смесь обеднена. На выходе из горелки струя расширяется, скорость потока W падает, а скорость U_n возрастает, так как исчезает охлаждающее действие стенок. И на каком-то расстоянии выполняется условие равенства скоростей

U_n = W.

В таких точках пламя удерживается стационарно, обеспечивая естественную стабилизацию факела. Пламя в процессе распространения от периферии к центру сносится потоком и в результате этого достигает оси струи на некотором расстоянии от устья горелки, образуя конусообразный факел.

Форма факела и его размеры зависят от скорости распространения пламени и скорости струи. Чем больше скорость распространения пламени U_n и чем меньше скорость потока W, тем короче факел.

Длина факела может быть вычислена (рис. 3.8) исходя из следующих соображений: пламя от периферии струи до оси горелки дойдет за время

D ,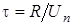

за это же время струя по оси потока пройдет расстояние

h = Dτ˙ W₀,

где W₀ – скорость потока на оси струи

R – радиус зажигающего кольца, практически равный диаметру устья горелки.

Тогда высота (длина) факела h может быть рассчитана как

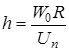. (3.13)

При уменьшении скорости истечения смеси из горелки высота конуса уменьшается. Когда скорость истечения смеси становится меньше скорости распространения пламени, может произойти проскок пламени в горелку.

Поэтому при переходе к горелкам большого размера необходимо увеличить скорость потока в соответствии с соотношением

.

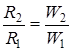Чем больше радиус горелки, тем больше должна быть скорость потока для предотвращения проскока пламени.

Условия отрыва и проскока в зависимости от коэффициента избытка воздуха изображены на рис. 3.9. Кривая, ограничивающая скорость проскока пламени в горелку, имеет такой же характер, как и зависимость скорости нормального распространения пламени. Действительно, чем выше скорость нормального распространения пламени, тем выше должна быть скорость истечения газа из горелки.

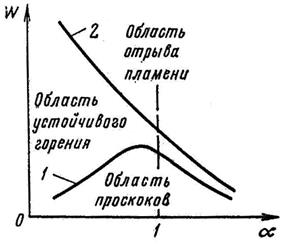
Рисунок 3.9 - Пределы устойчивости горения в горелках

Кривая отрыва имеет несколько иной характер. При коэффициенте избытка воздуха a >1 с увеличением скорости истечения газовоздушной среды (рис. 3.10,а) за счет расширения струи и падения скорости потока равенство скоростей и стабилизация горения установится на несколько большем расстоянии от устья горелки. При дальнейшем увеличении скорости потока точка зажигания ещё сместится от устья горелки. Но при какой–то скорости потока за счет разбавления смеси на периферии струи упадет значение U_n. В этом случае будет выполняться условие

W > U_n

и произойдет отрыв пламени от горелки (рис. 3.10 а).

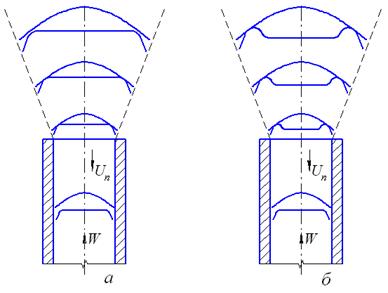
Рисунок 3.10 - Отрыв пламени при различных коэффициентах

избытка воздуха a: а - a>1; б - a<1

При коэффициенте избытка воздуха a<1 за счет разбавления смеси недостающим воздухом на периферии струи будет наблюдаться локальное увеличение скорости нормального распространения пламени (см. рис. 3.10 б). Это приводит к тому, что отрыв пламени наблюдается при больших скоростях потока.

Таким образом, чем меньше коэффициент избытка воздуха a в исходной смеси, тем шире диапазон скоростей, в котором горелка работает устойчиво. Именно поэтому часто используют горелки частичного смешения с a_исх = 0,4…0,7. Вести процесс при a < 0,4 нецелесообразно, так как может увеличиваться недожог топлива.