Минимизация логических функций

Логическую схему, реализующую заданный алгоритм преобразования сигналов, можно синтезировать непосредственно по выражению, представленному в виде СДНФ или СКНФ. Однако полученная при этом схема, как правило, не оптимальна с точки зрения ее практической реализации. Поэтому исходные функции алгебры логики обычно минимизируют.

Целью минимизации логической функции является уменьшение стоимости ее технической реализации.

Существует несколько способов минимизации, один из которых базируется на табличном виде представления функций алгебры логики. Он широко используется при минимизации функции алгебры логики, число переменных в которой обычно не превышает пяти. Свыше пяти переменных используют специально разработанные компьютерные методы минимизации логических функций.

Карта Вейча – это прямоугольная таблица, число клеток в которой для функции n-переменных равно 2ⁿ. Каждой из клеток поставлен в соответствие некоторый набор входных переменных, причем рядом расположенным клеткам соответствуют соседние наборы входных переменных (кодов), а в самих клетках записаны наборы значений функции, определенные для этих кодов.

Карта функции двух переменных приведена на рис. 1.4, а. Она содержит четыре клетки и является плоской фигурой. Для удобства использования по краям карты указаны значения входных переменных, которые для соответствующих строк и столбцов остаются постоянными. Набор переменных для заданной клетки таблицы определяется как совокупность аргументов, постоянных для строк и столбцов, на пересечении которых она расположена.

Карта Вейча функции трех переменных приведена на рис. 1.4, б. Она содержит восемь клеток. Наборы входных переменных, соответствующие крайним левому и правому столбцам, являются соседними. Поэтому данную карту удобно представить как поверх-ность цилиндра и она, в отличие от карты двух переменных, явля-ется объемной фигурой.

Карта Вейча функции четырех переменных приведена на рис. 1.4, в. Она содержит уже 16 клеток. Очевидно, что наборы входных переменных, соответствующие крайним столбцам, как и в карте функции трех переменных, являются соседними. Кроме этого соседние коды содержатся в нижней и верхней строках карты. Поэтому данная карта тоже является объемной фигурой и может быть представлена как поверхность тора.

При минимизации функции алгебры логики используют либо ее нулевые, либо единичные значения. В обоих случаях получают равносильные выражения, которые, однако, могут отличаться по числу членов и выполняемым логическим операциям.

Алгоритм минимизации функции алгебры логики сводится к следующему:

а) на карте Вейча функции алгебры логики n-переменных выделяют прямоугольные области, объединяющие выбранные значения функции (лог. 0 или лог. 1). Каждая область должна содержать 2^k клеток, где k – целое число. Области принято выделять, как показано на рис. 1.4. Выделенные области могут пересекаться, т.е. одна или несколько клеток могут включаться в различные области;

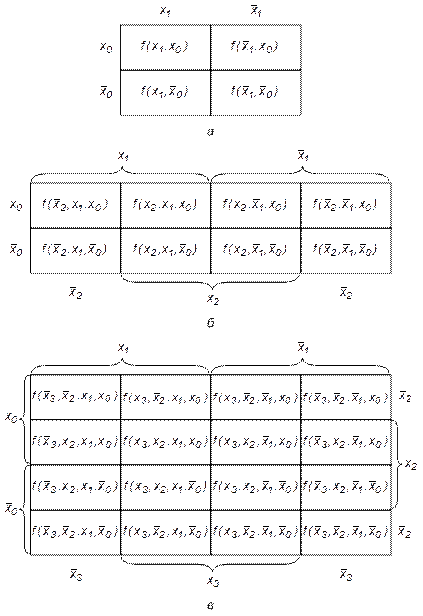
Рис. 1.4. Карта Вейча функции двух (а),

трех (б) и четырех (в) переменных

б) из полученного множества выбирают минимальное число максимально больших областей, включающих все выбранные значения функции алгебры логики;

в) каждая область описывается логическим произведением переменных или их инверсий. Если в область входит переменная и ее инверсия, это означает, что логическая функция в этой области не зависит от данной переменной. Поэтому такая переменная должна быть исключена из логического произведения, описывающего рассматриваемую область;

г) произведения переменных областей логически суммируют. Полученная сумма образует МДНФ.

При объединении клеток с единичным значением функции получают МДНФ самой функции, а при объединении клеток с ну-левыми значениями функции алгебры логики – МДНФ функции, инверсной заданной. Применив к полученной инверсной минимальной форме теоремы 12 и 16 (см. п. 1.1.2), можно получить минимальную конъюнктивную нормальную форму (МКНФ).

Пример 1.3. Минимизировать функцию вида

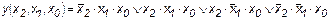
Решение. Составим карту Вейча

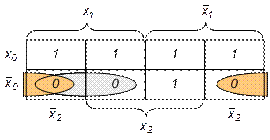
Запишем минимизированную функцию для нулевых значений.

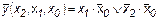
Воспользовавшись теоремами 12 и 16, найдем:

.

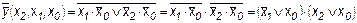Если к данному выражению применить теорему 18, то получим функцию

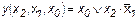
Из последнего примера видно, что при минимизации по ну-левым и единичным значениям функции первоначально можно определить равносильные, но не всегда одинаковые выражения. Различной будет и их техническая реализация. Используя теоремы алгебры логики, их можно преобразовать к единому виду. Для нахождения наиболее простого технического решения желательно проводить минимизацию как для нулевых, так и для единичных значений функции и из полученных выбирать простейшее.

Контрольные вопросы и задания

1. Объясните, что в цифровой электронной технике понимается под понятием кодовое слово. Что такое разряд кодового слова? Сколько комбинаций слов в 8-ми разрядном кодовом слове?

2. Дайте определение логическому (цифровому) устройству.

3. Перечислите и дайте объяснение 7-ми важнейшим логическим функциям двух переменных.

4. Докажите на выбор несколько из приведенных в п.1.1.2 теорем булевой алгебры.

5. Запишите совершенную дизъюнктивную нормальную форму (СДНФ) инверсии функции алгебры логики приведенной в комбинационной таблице в п.1.1.3.

6. Минимизируйте функцию вида

.

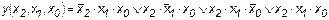По полученной минимизированной функции нарисуйте структурную схему логического устройства. Сравните ее с рис. 1.2, приведенным в примере 1.2.