Логические (Булевы) функции
Рассмотрим функции одной переменной y = f(x). Пронумеруем эти функции (их четыре) и расположим в виде таблицы:
| х | f0 | f1 | f2 | f3 |
Видно, что f0(х) = 0, a f3(х) = 1, т.е. эти две функции не зависят от х, f1(х) = х, т.е. она не меняет аргумента. Функция f2(х) действительно содержательная функция. Она принимает значения, противоположные значениям аргумента, обозначается 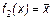 и называется отрицанием.
и называется отрицанием.
Рассмотрим функции двух переменных y = f(x1, x2).
Число этих функций равно 24 = 16. Пронумеруем и расположим их в естественном порядке.
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Рассмотрим более подробно эти функции. Две из них f0 = 0 и f15 = 1 являются константами. Функции
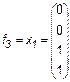 ,
, 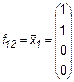 ,
, 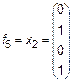 ,
, 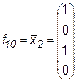
являются по существу функциями одной переменной.
Наиболее важные функции двух переменных имеют специальные названия и обозначения. Заметим, что эти обозначения не всегда общеприняты.
Перечислим семь важнейших функций.
1. Конъюнкция (функция И)
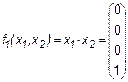 .
.
Конъюнкция (логическое умножение) переменных x1 и х2 равна лог. 1 в том случае, когда и x1 и х2 равны лог. 1 (отсюда и возникло название операции логическое И).
Конъюнкция – это фактически обычное умножение (нулей и единиц). Иногда эту функцию обозначают x1 & x2 или x1 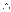 x2.
x2.
2. Дизъюнкция (функция ИЛИ)
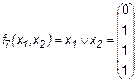 .
.
Дизъюнкция (логическое сложение) переменных x1 и х2 равна лог. 1, если или x1 или х2 равна лог. 1 (отсюда название операции логическое ИЛИ). В тех случаях, когда число переменных больше двух, их конъюнкция равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из переменных имеет значение лог. 1.
3. Импликация (следование)
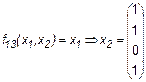 .
.
Иногда импликацию обозначают x1 כ х2 или x1 → х2 (читается “из x1 следует х2”).
Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если x1 = 0 (т. е. x1 “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если х2 = 1(т.е. х2 “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию.
4. Сложение по модулю 2, Исключающее ИЛИ (здесь и далее, если не оговорено противное, знаком “+” мы будем обозначать такое сложение):
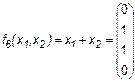 .
.
5. Эквивалентность или подобие ~
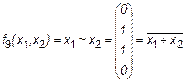 .
.
Эта f9 = 1 тогда и только тогда, когда х1 = х2.
6. Штрих Шеффера
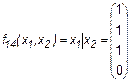 .
.
Иногда эту функцию называют “НЕ И” (так как она равна отрицанию конъюнкции).
7. Стрелка Пирса (иногда эту функцию называют штрих Лукасевича)
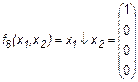 .
.
Эта функция является отрицанием дизъюнкции, и поэтому иногда ее называют “не ИЛИ”.
Заметим, что свойства последних двух функций похожи между собой и, может быть, поэтому в литературе их часто путают (т. е. называют f8 штрихом Шеффера, а f14 – стрелкой Пирса).
Три оставшиеся функции, (f2 , f4 и f11) особого значения в дискретной математике не имеют.
Операцию отрицания называют инверсией или дополнением. Для ее обозначения используют черту над соответствующим выражением. Операция определяется следующими постулатами:
если х = 1, то 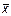 = 0, если х = 0, то
= 0, если х = 0, то 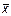 = 1.
= 1.
В математике установлен определенный порядок выполнения операций в сложном выражении. Подобно этому в сложном логическом выражении вначале выполняются операции инверсии, затем операции конъюнкции и в последнюю очередь операции дизъюнкции.
Теоремы булевой алгебры отражают связи, существующие между операциями, выполняемыми над логическими переменными. Сформулируем наиболее важные из них:
1. 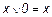 ;
;
2. 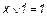 ;
;
3. 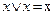 ;
;
4. 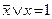 ;
;
5. 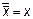 ;
;
6. 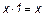 ;
;
7. 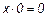 ;
;
8. 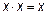 ;
;
9. 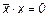 ;
;
10. 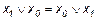 ;
;
11. 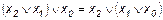 ;
;
12. 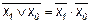 ;
;
13. 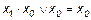 ;
;
14. 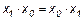 ;
;
15. 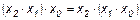 ;
;
16. 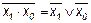 ;
;
17. 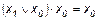 ;
;
18. 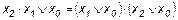 ;
;
19. 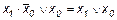 ;
;
20. 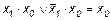
21. 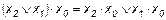 ;
;
22. 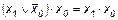 ;
;
23. 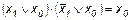
Справедливость всех перечисленных теорем может быть до-казана непосредственной подстановкой.
Дата добавления: 2015-05-05; просмотров: 940;
