Способы задания логических функций
В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функций). Для описания функций алгебры логики могут быть использованы различные способы. Основными из них являются описание функций в словесной форме, в виде таблиц истинности и алгебраических выражений.
Проиллюстрируем словесное описание функции алгебры логики на примере.
Логическая функция трех переменных равна 1, если хотя бы две входные переменные равны 1.
Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства.
Таблица, содержащая все возможные комбинации входных переменных xn-1 …x1x0 и соответствующие им значения выходных переменных yi, называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк и m+n столбцов, где n – количество входных сигналов, а m – выходных.
При описании функций алгебры логики алгебраическим выражением используются две стандартные формы ее представления – так называемые дизъюнктивная и конъюнктивная нормальные формы.
Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз.
ДНФ может быть получена из таблицы истинности с использованием следующего алгоритма:
а) для каждого набора переменных, на котором функция алгебры логики равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы;
б) логически суммируют все конституенты единицы.
ДНФ, полученную суммированием конституент единицы, называют совершенной (СДНФ).
Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз.
КНФ может быть получена из таблицы истинности с использованием следующего алгоритма:
а) для каждого набора переменных, на котором функция алгебры логики равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля;
б) логически перемножают все полученные конституенты нуля.
КНФ, полученную суммированием конституент нуля, также называют совершенной (СКНФ).
Пример 1.1. Запишите дизъюнктивную и конъюнктивную нормальные формы для следующей таблицы истинности:
| x2 | x1 | x0 | y |
Решение. Согласно приведенному выше алгоритму дизъюнктивная нормальная форма примет вид
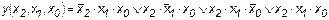 , (1.1)
, (1.1)
а конъюнктивная нормальная форма определится как
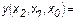
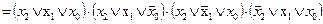 . (1.2)
. (1.2)
Иногда удобнее применять не саму функцию алгебры логики, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ – единичные значения функции.
Дата добавления: 2015-05-05; просмотров: 1845;
