Расчет дисперсии одномодовых световодов

В одномодовых световодах распространяется только одна мода НЕ₁₁(LP₀₁) и σ = σ_вн, т.е уширение импульса определяется дисперсией материала и волноводной дисперсией.

Согласно (1.11)

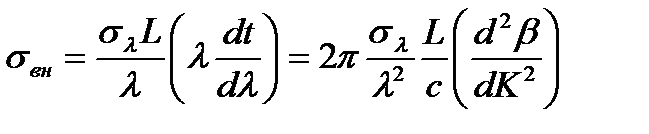(2.1)

где t – коэффициент группового замедления основной моды, λ – средняя длина волны излучения, β – продольная постоянная распространения моды НЕ₁₁(LP₀₁).

Для сокращения записи индексы «01» у t и β, а также «0» у λ в (2.1) и ниже опущены.

Дисперсионной характеристикой моды называют зависимость β от частоты или длины волны. Для оптических световодов ее часто рассматривают в нормированном виде, как зависимость нормированной постоянной распространения b от нормированной частоты V. Здесь

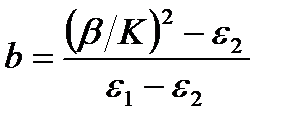(2.2)

V было введено в разделе 1; ε₁ = n₁² – наибольшее значение диэлектрической проницаемости в сердцевине световода ( в общем случае ε изменяется в поперечном сечении сердцевины по закону ε(ρ)), ε₂ = n₂² – диэлектрическая проницаемость оболочки, n₁ и n₂ – соответствующие ε₁ и ε₂ показатели преломления, а – радиус сердцевины световода, ρ = r / a – нормированная радиальная координата.

Целесообразность использования нормированной характеристики b(V) заключается в том, что при малых относительных разностях показателей преломления Δ вид характеристики не зависит от Δ, а определяется лишь нормированным профилем диэлектрической проницаемости 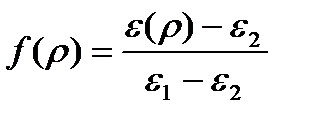. Так, для двухслойных однородных световодов 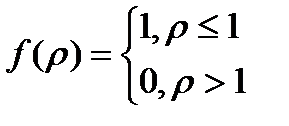, и независимо от Δ дисперсионной характеристикой моды LP₀₁ является кривая 1 на рис.2.1. Из соотношения (2.2)

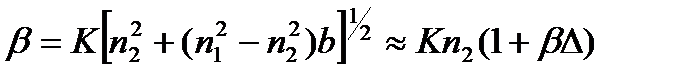(2.3)

Последнее приближение получено из условия, что в световодах b < 1, Δ << 1, а следовательно bΔ << 1. Из (2.3)

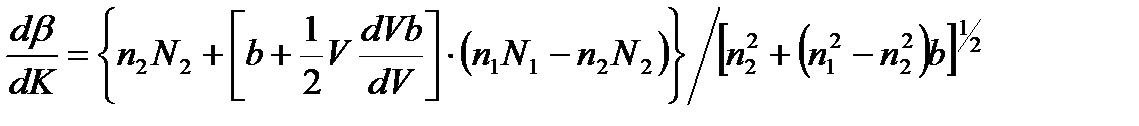(2.4)

где 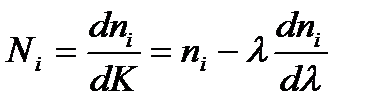- (2.5)

групповой показатель преломления в материале с n₁ (і = 1) и в материале оболочки (і = 2).

Если

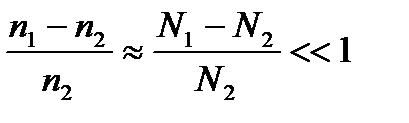(2.6)

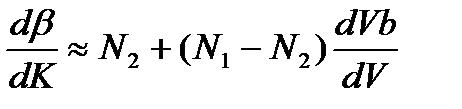то (2.7)

Дифференцируя (2.4) по К и учитывая, что bΔ << 1, получим

σ_вн = σ_λ × L·(Т₁ + Т₂ + Т₃) (2.8)

где 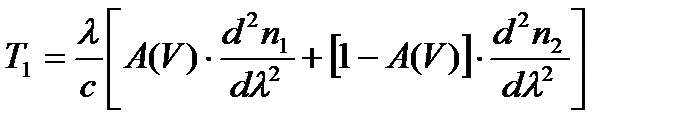- составная дисперсия материала .

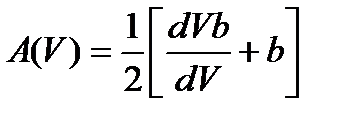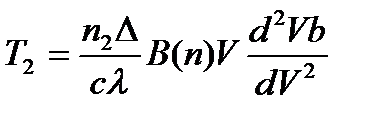- составная волноводная дисперсия,

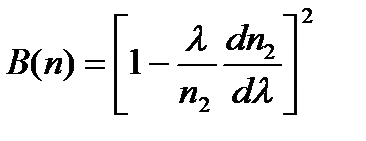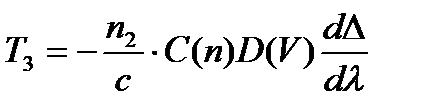, - дисперсия профиля показателя преломления,

,

.

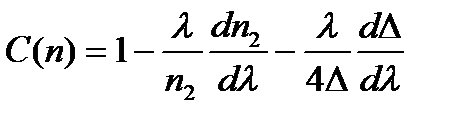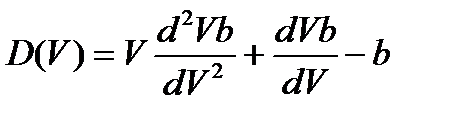Основной вклад вносят члены Т₁ и Т₂, определяющиеся соответственно дисперсией материала и волноводной дисперсией.

Если материалы сердцевины и оболочки удовлетворяют условие (2.6), то используя (2.7), получим

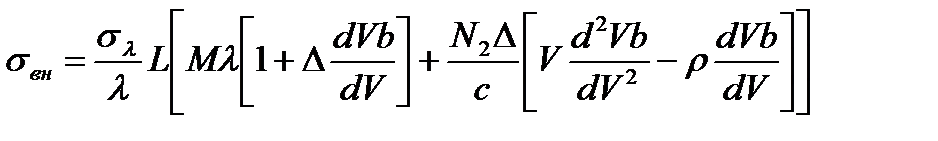(2.9)

где 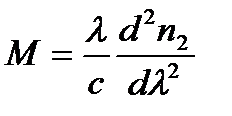- удельная материальная дисперсия стекла оболочки световода.

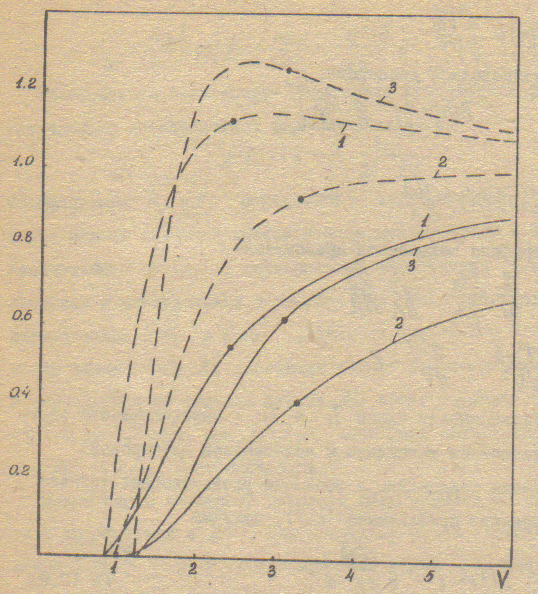
Рис. 2.1. Зависимости нормированных постоянной распространения b (сплошные кривые) и времени пробега dVb/dV (штриховые кривые) моды LP₀₁ от нормированной частоты. Точкой на кривой обозначена граница одномодового режима – частота отсечки моды LP₁₁:

1 – однородный двухслойный световод,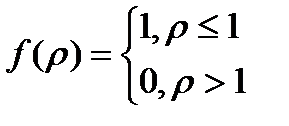

2 – параболический световод,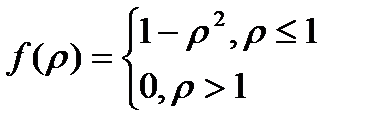

3 – светодиод W-типа, .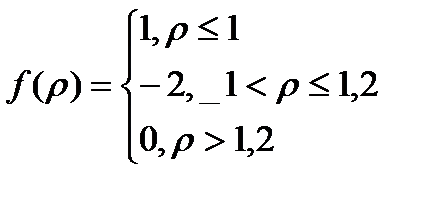

Параметр 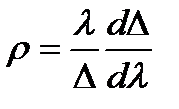мал. Так, для световодов, легированных германием ρ ≈ 0,1 при λ = 1,55 мкм; ρ ≈ 0,06 при λ = 1,3 мкм. При малых Δ и на коротких длинах волн (λ < 1мкм) можно считать, что ρ ≈ 0 и 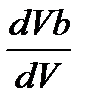≈0. Тогда из (2.9) для расчета среднеквадратического уширения основной моды получим соотношение

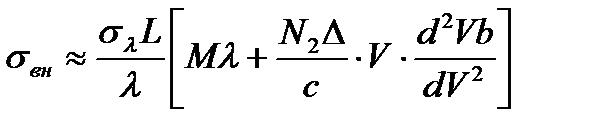(2.10)

Спектральную зависимость показателя преломления можно описать трехчленной дисперсионной формулой Селейера

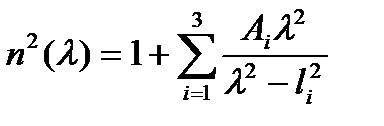(2.11)

Коэффициенты А_i и l_i определяются экспериментально.

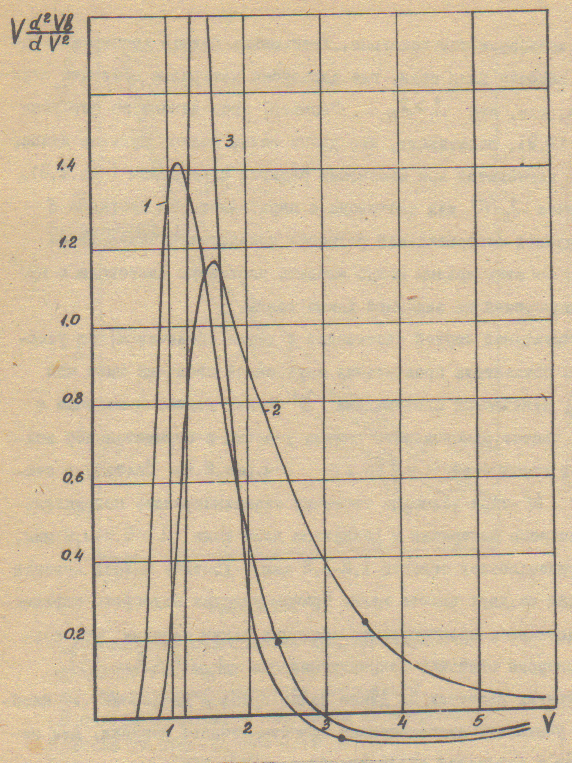
Рис. 2.2. Волноводная дисперсия моды LP₀₁ в световодах, дисперсионные кривые которых представлены на рис. 2.1. Точкой на кривой обозначена граница одномодового режима.

1- однородный двухслойный световод, 2 - параболический световод,

3 – световод W-типа.

Волноводная дисперсия основной моды зависит РТ профиля показателя преломления и Δ. Для некоторых типов световодов зависимость V 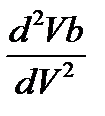от V представлении на рис. 2.2. Точки на кривой указывают частоту отсечки моды LP₁₁, определяющую верхнюю частоту полосы частот одномодового режима. Для световода с параболическим профилем показателя преломления V 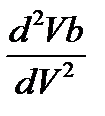положительна для всех V. Для однородного волновода при V < 3 волноводная дисперсия положительна, для V > 3 – отрицательна. В рабочей области частот одномодового режима (V = 1,2-2,4) V 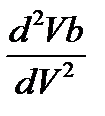изменяется от 1,4 до 0,005. Зависимости V 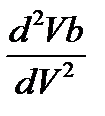в световодах со степенным профилем диэлектрической проницаемости f(ρ) = 1- ρ^g для g > 2 располагается между кривыми g = 2 (параболический волновод) и g = ∞ (однородный двухслойный волновод).

В области одномодового режима волноводная дисперсия рассмотренных светодиодов положительна. Уменьшение полной дисперсии возможно в области длин волн, где дисперсия материала оболочки отрицательна, т.е. при λ > λ_М^. Расчеты, проведенные по формулам (2.8), (2.9), показывают, что длина волны полной нулевой дисперсии λ_n изменяется при изменении радиуса сердцевины (рис. 2.5). Зависимости λ_n(а) для световода с параболическим профилем ε при различной относительной разности показателей преломления показаны на рис. 2.4. По этим кривым можно выбрать параметры световода с нулевой дисперсией на заданной длине волны.

Отличительной чертой световодов с двумя оболочками (при условии, что показатель преломления внутренней оболочки ниже, чем внешней), называемых световодами W-типа, является наличие в области частот одномодового режима участка с отрицательной волноводной дисперсией V 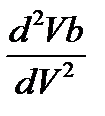< 0 (см. рис. 2.2). Поэтому в световодах W-типа возможно частично скомпенсировать положительную дисперсию материала в диапазоне длин волн λ = 0,8 - 0,9 мкм, а в длинноволновой области 1,2 – 1,6 мкм – достичь полной нулевой дисперсии на двух длинах волн. Причем удается подобрать параметры сердцевины и промежуточной оболочки таким образом, что полная дисперсия близка к нулю в диапазоне λ_n1 <λ < λ_n2.

В строгих расчетах на длине волны нулевой дисперсии λ_n необходимо учитывать дисперсионные эффекты второго порядка. Для источников с гауссовой спектральной кривой

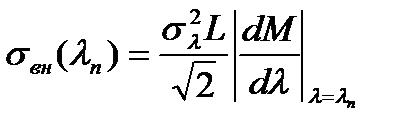
Типичное значение производной |dM/dλ| приближенно равно 0,1 пс/(км·нм²).

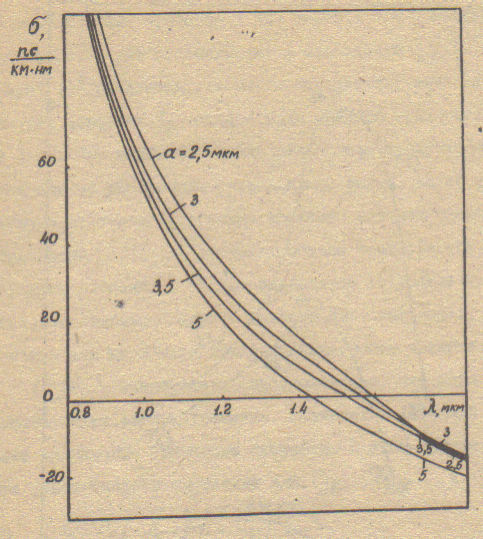
Рис. 2.3. Спектральная зависимость среднеквадратичного уширения импульсов в параболическом световоде при различных радиусах сердцевины

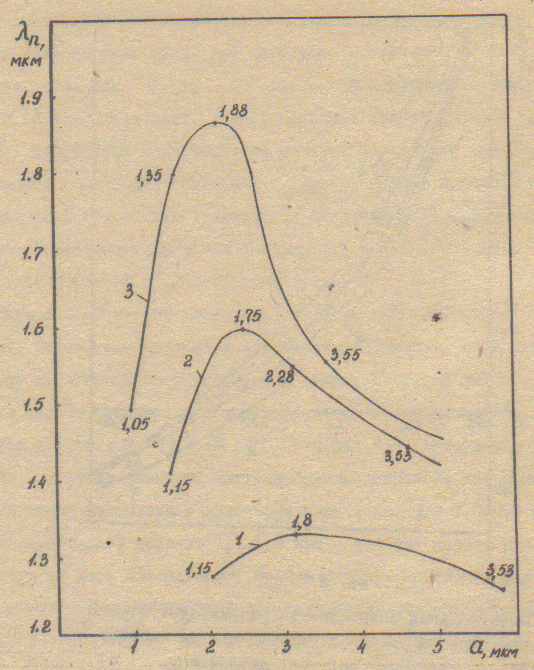
Рис. 2.4. Зависимость длины волны нулевой полной дисперсии от радиуса сердцевины в световоде с параболическим профилем ε:

1 – Δ = 0,37%; 2 – Δ = 0,755%; 3 – Δ = 1,48%.

Точками и цифрами на кривых указаны значения нормированной частоты V.