Расчет уширения импульсов в многомодовых световодах
В многомодовых световодах для расчета σ(L) необходимо учитывать в (1.9) обе составляющие – межмодовую σмеж(L) и внутримодовую σвн(L) дисперсии. Их можно определить, вычислив время групповой задержки tlm каждой моды, распространяющейся на частоте V. При малом изменении показателя преломления внутри сердцевины на расстоянии равном длине волны, малой Δ, анализ многомодовых световодов можно провести методом Вентцеля-Крамерса-Бриллюэна. В расчетах обычно предполагают, что моды возбуждены равномерно, имеют одинаковое затухание и распространяются, не связываясь друг с другом. Для световодов, нормированное изменение диэлектрической проницаемости которых имеет вид f(ρ) = 1- ρg, справедливо предположение, что моды с одинаковыми постоянными распространения, а значит и фазовыми скоростями, имеют одинаковые групповые скорости. В этом случае удается найти аналитическое выражение для tlm, σмеж(L) и σвн(L).
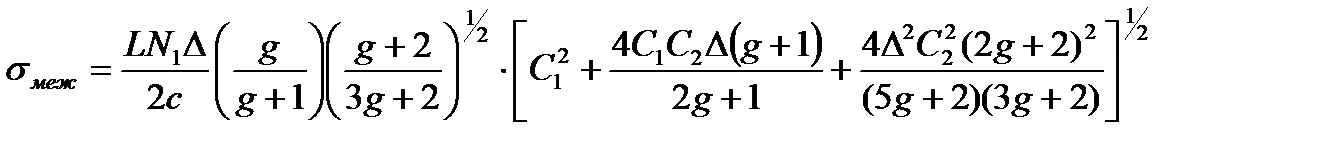 (3.1)
(3.1)
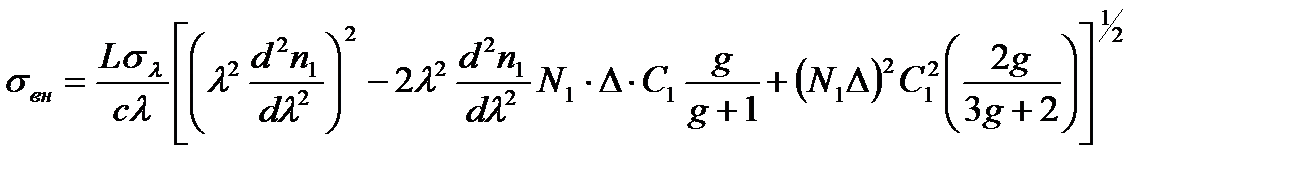 (3.2)
(3.2)
где L – длина световода, 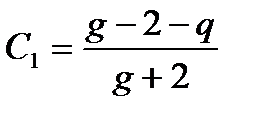 ,
, 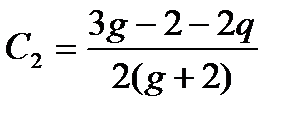 . Параметр
. Параметр 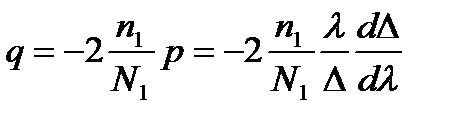 учитывает различие дисперсионных свойств материалов сердцевины и оболочки световода.
учитывает различие дисперсионных свойств материалов сердцевины и оболочки световода.
Минимальное значение σмеж, а следовательно, и σ, достигается при показателе степени профиля
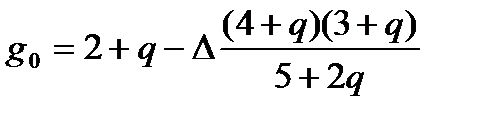 (3.3)
(3.3)
При q = 0 (без учета дисперсии Δ) g0 = 2. Зависимость g0 от длины волны для световодов, легированных фосфором и германием, представлена на рис. 3.1. Сплошные кривые немного отличаются от штриховых, но показывают, что оптимальное значение g0 меняется на 10-15% в диапазоне длин волн λ = 0,6 – 1,6 мкм.
При оптимальном значении g0
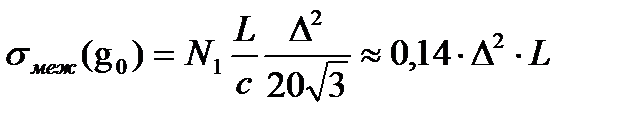 (мкс),
(мкс),
что при тех же Δ в 10/Δ раз меньше, чем в однородном двухслойном световоде, которому соответствует g = ∞.
Для типичного значения Δ = 0,01 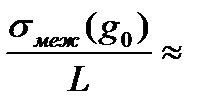 0,14·10-4 мкс/км = 0,014 нс/км, для однородного световода
0,14·10-4 мкс/км = 0,014 нс/км, для однородного световода 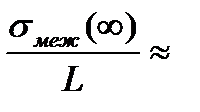 14 нс/км. Однако полное уширение импульса σ для оптимального g0 больше вычисленного σмеж и определяется σвн, т.е. дисперсией материала и волноводной дисперсией, а также шириной спектральной линии источника.
14 нс/км. Однако полное уширение импульса σ для оптимального g0 больше вычисленного σмеж и определяется σвн, т.е. дисперсией материала и волноводной дисперсией, а также шириной спектральной линии источника.
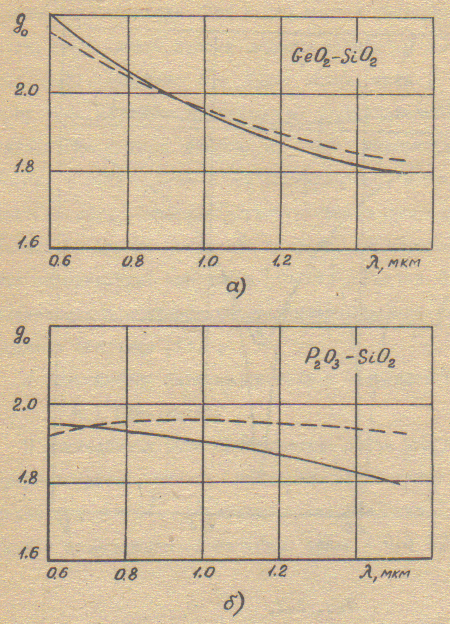
Рис. 3.1. Спектральная зависимость оптимального показателя степени в профиле диэлектрической проницаемости в световодах, легированных германием (а) и фосфором (б)
На рис. 3.2 представлены рассчитанные по (3.1) и (3.2) зависимости полной среднеквадратичной ширины σ в световоде из кварцевого стекла с добавкой титана, имеющего апертуру 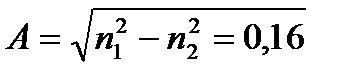 на длине волны λ = 0,9 мкм, для трех различных источнков. Кривая 1 рассчитана для светодиода на арсениде галлия, кривая 2 – инжекционного лазера и кривая 3 – для лазера с распределенной обратной связью. Штриховая линия соответствует нулевой материальной дисперсии световода. При малой ширине спектральной линии зависимость σ(g) имеет резкий минимум вблизи g ≈ 2 (кривые 2 и 3 на рис. 3.2). Уширение σ будет малым, если g близко к оптимальному. При массовом производстве при существующем уровне развития технологии жесткие допуски на g выдержать трудно.
на длине волны λ = 0,9 мкм, для трех различных источнков. Кривая 1 рассчитана для светодиода на арсениде галлия, кривая 2 – инжекционного лазера и кривая 3 – для лазера с распределенной обратной связью. Штриховая линия соответствует нулевой материальной дисперсии световода. При малой ширине спектральной линии зависимость σ(g) имеет резкий минимум вблизи g ≈ 2 (кривые 2 и 3 на рис. 3.2). Уширение σ будет малым, если g близко к оптимальному. При массовом производстве при существующем уровне развития технологии жесткие допуски на g выдержать трудно.
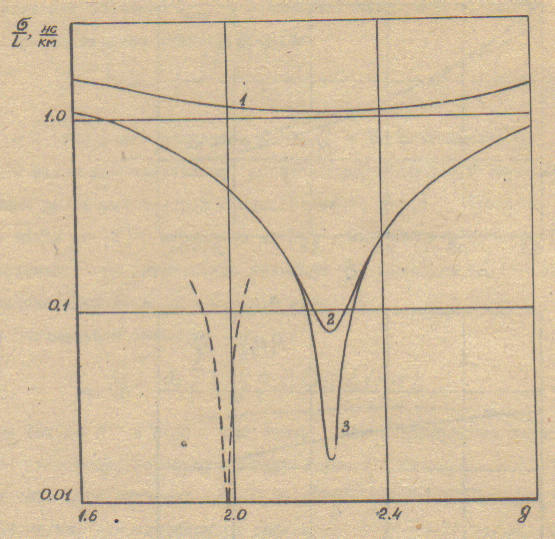
Рис. 3.2. Зависимость среднеквадратичного уширения импульсов от показателя степени профиля для трех различных источников
1 – светодиода на арсениде галлия,
2 – инжекционного лазера
3 – для лазера с распределенной обратной связью.
Штриховая кривая соответствует нулевой материальной дисперсии.
Наряду с отклонением g от оптимального, возможно появление осевого провала в профиле диэлектрической проницаемости, синусоидальные и другие искажения профиля, вызывающие увеличение уширения передаваемых импульсов. Расчет σ в многомодовых световодах с искажениями степенного профиля f(ρ) = 1- ρg производится численно.
У большинства изготавливаемых в настоящее время световодов
B·L ≤ 1 Гбит·км/с.
В приведенных выше соотношениях связь моднее учитывалась и предполагалось, что σ пропорционально длине световода. При связи мод σ ≈ Lγ, теоретическое значение γ = 0,5; на практике в зависимости от величины связи -0,5 ≤ γ ≤ 1.
Дата добавления: 2015-05-05; просмотров: 1073;
