Уширение импульсов в световодах

При малых разностях показателей преломления сердцевины и оболочки световода вдоль него возможно распространение линейно-поляризованных мод LP_lm. Азимутальный индекс l и радиальный m характеризуют распределение поля в поперечном сечении световода.

Расчеты показывают, что продольные постоянные распространения мод β_lm различны и зависят от профиля показателя преломления, значения нормированной частоты 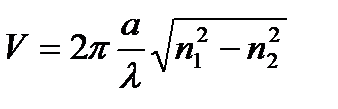и относительной разности показателей преломления сердцевины и оболочки Δ. Здесь а – радиус сердцевины световода, λ – длина волны, n₁ – наибольшее значение показателя преломления сердцевины, n₂ – показатель преломления оболочки, .

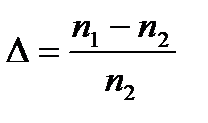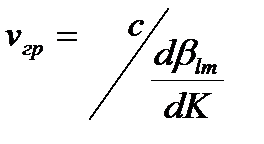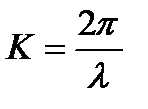Групповая скорость моды волновода , где - волновое число, с – скорость света в вакууме; следовательно отрезок световода длиной 1 км мода LP_lm пройдет за время 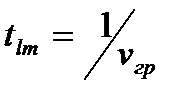, а отрезок длиной Z км – за время 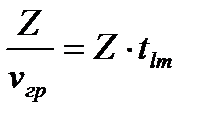. Время t_lm называется коэффициентом группового замедления моды. Если на входном конце световода длиной Z мощность моды описывается функцией P_lm(λ,Z)×δ(t), то импульс на выходном конце можно определить суммированием по всем модам

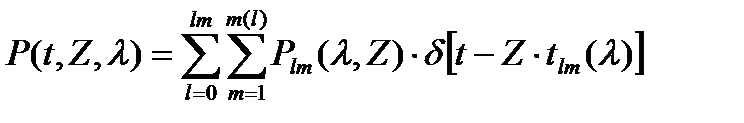(1.1)

где m(l) – наибольший радиальный индекс у моды с заданным азимутальным индексом, l_m – наибольший азимутальный индекс у мод, распространяющихся на частоте V, δ(t) – δ-функция Дирака. Далее двойная сумма обозначается одним значком с указанием индексов, по которым производится суммирование.

Зависимость мощности от длины волны в основном определяется спектральной линией источника – спектральным распределением мощности источника S(λ). Тогда 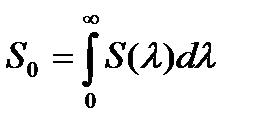- полная мощность источника, 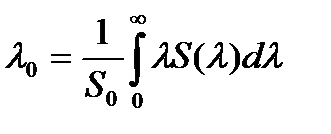- средняя длина волны излучения, 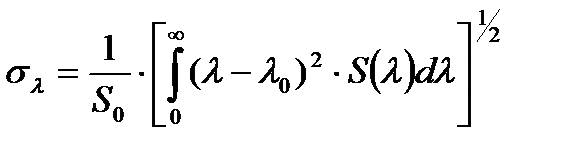- среднеквадратическая ширина спектральной линии источника.

Полупроводниковые лазеры и светодиоды излучают обычно в узкой полосе длин волн. Для светодиодов - σ_λ = 15…100 нм, для лазеров σ_λ = = 0,1…4 нм. В такой узкой области длин волн чувствительность фотодетекторов можно считать постоянной. Следовательно, на выходном конце световода необходимо рассмотреть распределение

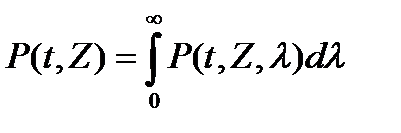(1.2)

Величину

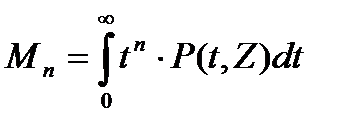(1.3)

называют моментом п-го порядка распределения Р(t,Z). Подставляя Р(t,Z) из (1.2) и учитывая (1.1) получим

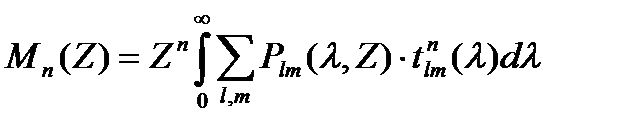(1.4)

Определим М_п(Z). Для этого мощность каждой моды представим в виде

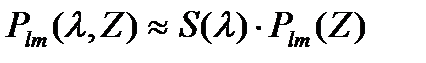(1.5)

и разложим коэффициент группового замедления t_lm в ряд Тейлоора в окрестности λ₀:

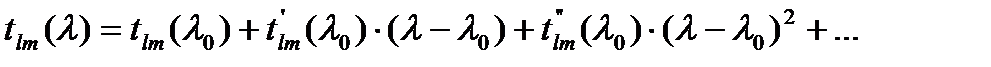(1.6)

Здесь штрихи обозначают производные по λ в точке λ = λ₀.

Подставляя (1.5), (1.6) в (1.4) и используя определения λ₀ и σ_λ, получим выражение для n-го момента

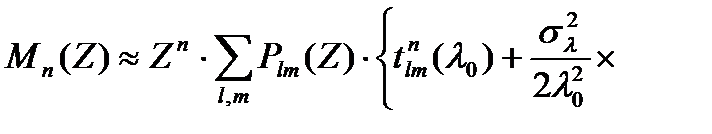
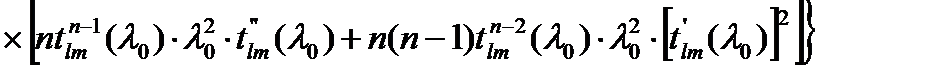(1.7)

Так как 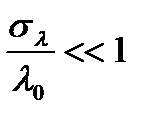, члены порядка 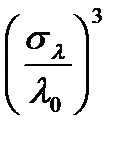и выше в (1.7) опущены. Это уравнение может быть записано проще, если ввести определение 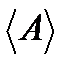- средней величины по модовому распределению

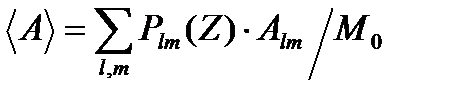(1.8)

Тогда нормированный момент 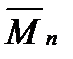определяется выражением

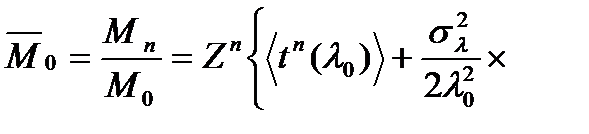
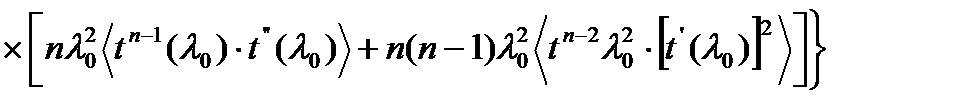
При n = 0 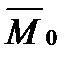= 1. Средняя величина времени распространения импульса от входного конца световода до его сечения с координатой Z равно 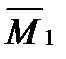, т.е.

.

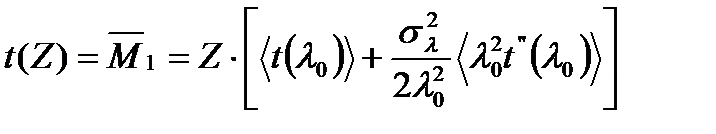Информационную емкость световода возможно определить с помощью среднеквадратического значения уширения импульса σ(Z). С учетом введенных обозначений

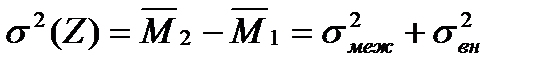(1.9)

где

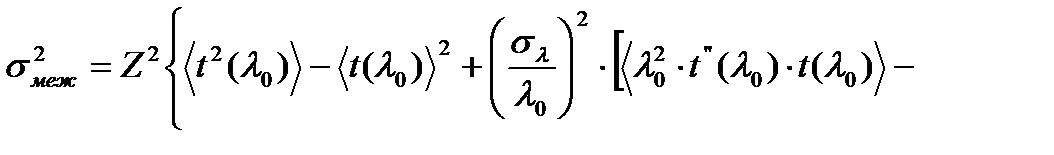
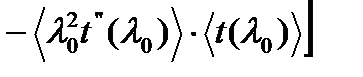(1.10)

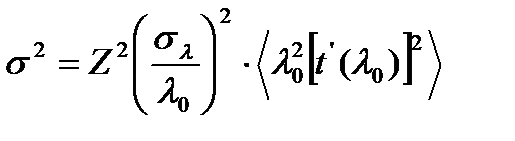(1.11)

Среднеквадратическое уширение импульса разбито на две части – межодовое уширение σ_меж и внутримодовое σ_вн. Межмодовое (иногда его называют модовым) уширение импульса возникает из-за различия групповых скоростей мод.

Дополнительное слагаемое в правой части 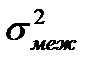, определяемое относительной спектральной шириной линий источника, мало и им можно пренебречь.

Внутримодовое уширение σ_вн представляет собой среднее уширение импульса в пределах каждой моды. Оно вызвано дисперсией материала, определяемой зависимостью показателя преломления материала от длины волны, и волноводной дисперсией, обусловленной зависимостью групповой скорости моды в световоде от длины волны. В одномодовом режиме иногда необходимо учитывать также поляризационную дисперсию, вызванную различием групповых скоростей взаимноортогональных квазивыродженных поляризаций основной моды. Поляризационная дисперсия на порядок меньше дисперсии материала и волноводной дисперсии.

При цифровой (например, импульсно-кодовой) модуляции наибольшая скорость передачи информации В определяется среднеквадратичной шириной импульса σ(L)

B ≈ 0,25/ σ(L) (1.12)

Здесь L – длина световода.

Зная σ(L), можно найти также полосу пропускания световода П. Последняя, выраженная в Гц, по величине приближенно равна скорости передачи информации в бит/с, т.е. П ≈ B ≈ 0,25/ σ(L).

Следовательно, основной целью расчета дисперсии в волоконных световодах, предназначенных для передачи информации, является определение σ(L).