Проверка однородности совокупности дисперсий
Для каждого слоя вычисляется несмещенная оценка дисперсии, обозначим эти оценки через μ*2(x) , μ*2 (y), …, μ*2 (w) соответственно. Числа степеней свободы этих оценок
k1 = п1–1, k2 = п2 – 1, …, kт = пw–1.
Гипотеза Н0 состоит в том, что выборки, по которым определены оценки дисперсии, получены из генеральных совокупностей, обладающих одинаковыми дисперсиями
μ2(x)= μ2(y)= … =μ2(w)= μ2,
при этом величина дисперсии μ2 остается неизвестной. Следует выяснить, являются ли величины μ*2(x) , μ*2 (y), …, μ*2 (w) оценками одной и той же генеральной дисперсии μ2.
Рассмотрим сначала случай, когда объем выборок по слоям хотя бы частично различается. В такой ситуации применяется критерий однородности Бартлетта. Проверка однородности реализуется в несколько шагов.
Вычисляется усредненная оценка несмещенной дисперсии по всем слоям
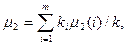
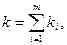 (6.4)
(6.4)
где μ*2(i) – несмещенная оценка дисперсии для слоя i.
Рассчитывается значение критерия
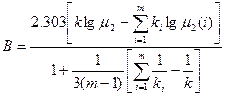 (6.5)
(6.5)
Бартлетт установил, что случайная величина В при условии справедливости нулевой гипотезы распределена приближенно как хи-квадрат с т–1 степенями свободы, если все ni больше трех. По заданному уровню значимости a, числу степеней свободы т–1 для правосторонней критической области определяется критическое значение с2кр(m-1;a). Если соблюдается условие
B< с2кр(m-1;a),
то нет оснований отвергнуть нулевую гипотезу. Если B > с2кр(m-1;a), то нулевая гипотеза отвергается. Критерий Бартлетта чувствителен к отклонениям распределения от нормального, поэтому к результатам сравнения следует относится осторожно, а при одинаковом объеме всех слоев вместо критерия Бартлетта лучше применять критерий Кочрена (Кохрена).
Итак, если k1 = k2 = … = kт, то применяется критерий Кочрена
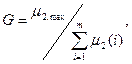 (6.6)
(6.6)
где μ2, max – максимальная оценка дисперсии по всем слоям.
Критическая область для критерия Кочрена правосторонняя. Критическую точку Gкр(k1,m;a) находят по таблице распределения Кочрена, фрагмент которой приведен в табл. Критическая область определяется неравенством G > Gкр(k1,m;a) .
Дата добавления: 2015-05-05; просмотров: 1071;
