Постановка задачи. Одной из типовых задач обработки многомерных ЭД является определение количественной зависимости показателей качества объекта от значений его параметров и

Одной из типовых задач обработки многомерных ЭД является определение количественной зависимости показателей качества объекта от значений его параметров и характеристик внешней среды. Примером такой постановки задачи является установление зависимости между временем обработки запросов к базе данных и интенсивностью входного потока. Время обработки зависит от многих факторов, в том числе от размещения искомой информации на внешних носителях, сложности запроса. Следовательно, время обработки конкретного запроса можно считать случайной величиной. Но вместе с тем, при увеличении интенсивности потока запросов следует ожидать возрастания его среднего значения, т.е. считать, что время обработки и интенсивность потока запросов связаны корреляционной зависимостью.

Постановка задачи регрессионного анализа формулируется следующим образом.

Имеется совокупность результатов наблюдений вида (7.1). В этой совокупности один столбец соответствует показателю, для которого необходимо установить функциональную зависимость с параметрами объекта и среды, представленными остальными столбцами. Будем обозначать показатель через y* и считать, что ему соответствует первый столбец матрицы наблюдений. Остальные т–1 (m > 1) столбцов соответствуют параметрам (факторам) х₂, х₃, …, х_т .

Требуется: установить количественную взаимосвязь между показателем и факторами. В таком случае задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y* = f(x₂ , x₃ , …, x_т), которая наилучшим образом описывает имеющиеся экспериментальные данные.

Допущения:

· количество наблюдений достаточно для проявления статистических закономерностей относительно факторов и их взаимосвязей;

· обрабатываемые ЭД содержат некоторые ошибки (помехи), обусловленные погрешностями измерений, воздействием неучтенных случайных факторов;

· матрица результатов наблюдений является единственной информацией об изучаемом объекте, имеющейся в распоряжении перед началом исследования.

Функция f(x₂ , x₃ , …, x_т), описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии. Термин "регрессия" (regression (лат.) – отступление, возврат к чему-либо) связан со спецификой одной из конкретных задач, решенных на стадии становления метода. Его ввел английский статистик Ф. Гальтон. Он исследовал влияние роста родителей и более отдаленных предков на рост детей. По его модели рост ребенка определяется наполовину родителями, на четверть – дедом с бабкой, на одну восьмую прадедом и прабабкой и т.д. Другими словами, такая модель характеризует движение назад по генеалогическому дереву. Ф. Гальтон назвал это явление регрессией как противоположное движению вперед – прогрессу. В настоящее время термин "регрессия" применяется в более широком плане – для описания любой статистической связи между случайными величинами.

Решение задачи регрессионного анализа целесообразно разбить на несколько этапов:

· предварительная обработка ЭД;

· выбор вида уравнений регрессии;

· вычисление коэффициентов уравнения регрессии;

· проверка адекватности построенной функции результатам наблюдений.

Предварительная обработка включает стандартизацию матрицы ЭД, расчет коэффициентов корреляции, проверку их значимости и исключение из рассмотрения незначимых параметров (эти преобразования были рассмотрены в рамках корреляционного анализа). В результате преобразований будут получены стандартизованная матрица наблюдений U (через y будем обозначать стандартизованную величину y*) и корреляционная матрица r.

Стандартизованной матрице U можно сопоставить одну из следующих геометрических интерпретаций:

· в т-мерном пространстве оси соответствуют отдельным параметрам и показателю. Каждая строка матрицы представляет вектор в этом пространстве, а вся матрица – совокупность п векторов в пространстве параметров;

· в п-мерном пространстве оси соответствуют результатам отдельных наблюдений. Каждый столбец матрицы – вектор в пространстве наблюдений. Все вектора в этом пространстве имеют одинаковую длину, равную 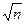. Тогда угол между двумя векторами характеризует взаимосвязь соответствующих величин. И чем меньше угол, тем теснее связь (тем больше коэффициент корреляции).

В корреляционной матрице особую роль играют элементы левого столбца – они характеризуют наличие или отсутствие линейной зависимости между соответствующим параметром u_i (i =2, 3, …, т) и показателем объекта y. Проверка значимости позволяет выявить такие параметры, которые следует исключить из рассмотрения при формировании линейной функциональной зависимости, и тем самым упростить последующую обработку.